Вид выборки. Простая случайная выборка (простой рандомизированный отбор). При этом любая единица выборки имеет равные шансы быть отобранной с помощью жеребьевки, таблиц или компьютерного генератора случайных чисел.
1. Известна численность генеральной совокупности. Обычно эти данные можно получить из результатов переписи населения, отчетности статорганов, в которых указывается возрастной, половой, социальный и т.д. состав определенного региона (района, города, страны).
Для количественных признаков
(97)
Где N – объем генеральной совокупности
Δ ошибка выборки это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности, также как и уровень значимости ошибка выборки задается самим исследователем. Ее предварительная оценка (предпочитаемая величина перед подстановкой в формулу) часто произвольна. Как правило, не рекомендуется принимать ошибку выборки выше 5%.
Для номинальных и порядковых признаков (доли объектов с заданным признаком)
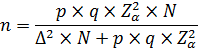(98)
где q=1p,
p подбирается эмпирическим путем, или как крайний случай p =0,5 и q =0,5
При неизвестной численности генеральной совокупности для количественных признаков
(99)
Для случая определения доли
(100)
Вид выборки. Стратифицированный способ отбора все объекты разделяют на классы, именуемые слоями (стратами), в зависимости от изучаемых характеристик, таких как возраст, пол и т.п., после чего из каждого слоя отбирается простая случайная выборка с одинаковой или специально рассчитанной (для каждого слоя) выборочной долей
1. Объем генеральной совокупности известен
Признак количеcтвенный
Общий объем выборки определяется как
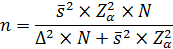(101)
где
– средняя внутригрупповая дисперсия (102)
Ni число объектов в каждом из классов генеральной совокупности
Тогда выборка из каждого класса имеет численность пропорциональную представительству в генеральной совокупности
(103)
Но более оптимальным является распределение выборки по классам с учетом вариабельности признака в этих классах
(104)
Признак качественный (частота встречаемости)
(105)
где
– средняя внутригрупповая дисперсия (106)
где pi и qi – доля и обратная ей величина в каждом из классов генеральной совокупности (как крайний случай p =0,5 и q =0,5).
Ni число объектов в каждом из классов генеральной совокупности
2. При неизвестной численности генеральной совокупности для количественных признаков
(107)
