Декартово произведение множеств. В математике достаточно часто приходится иметь дело не только с отдельными элементами какого-либо множества

В математике достаточно часто приходится иметь дело не только с отдельными элементами какого-либо множества, но и с упорядоченными парами его элементов. Примерами упорядоченных пар могут служить (a, b), (1, 1). В упорядоченных парах числа могут совпадать, а могут и не совпадать. Аналогично сказанному можно ввести в рассмотрение упорядоченные тройки, упорядоченные четверки, а в общем случае и упорядоченные наборы длины n элементов данного множества.

Набор, составленный из элементов a ₁, a ₂,... a_n, n = 2,3,... взятых именно в этом порядке, будем обозначать (a ₁,..., a_n) и говорить, что i -я компонента этого набора есть a_i. Длиной набора (a ₁,..., a_n) будем называть число n его компонент.

Определение 8.

Два набора равны между собой, т. е. (a ₁ ,...,a_n) = (b ₁ ,...,b_n), тогда и только тогда, когда для любого i выполнено равенство a_i=b_i.

ПРИМЕР 8.

(a, a, b) (a, b, a); (a, 2) (a, 2, 2).

Условимся называть элемент a некоторого множества A набором длины один, тогда можно ввести пустой набор - набор длины нуль, который мы будем обозначать .

Определение 9.

Декартовым (прямым) произведением множеств A ₁ ,..., A_n (n 2) называется множество, состоящее из всех тех и только тех наборов длины n, i-я компонента которых принадлежит множеству A_i:

.

Через обозначают декартово произведение n – штук множеств M. Его элементами являются упорядоченные наборы из n элементов, каждый из которых принадлежит множеству M. Множество еще называют n -й декартовой степенью множества M. По аналогии с числами обычно полагают , = .

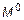ПРИМЕР 9.

Рассмотрим два множества A ₁ = [0, 1], A ₂ = [2, 3]. Если на плоскости выбрать некоторую декартову систему координат, то прямое произведение A ₁× A ₂ можно представить как квадрат со стороной длины 1 (рис. 6).

Очевидно, что «декартовая плоскость», известная нам со школы определяется как Декартово произведение множества действительных чисел . В дальнейшем при изучении функций двух переменных, в отличие от функции одной переменной, нам потребуется находить область определения как некоторую часть декартовой плоскости. В этом случае диаграммы Венна получат большую наглядность и будут представлены кривыми второго порядка.

Заключение

В лекции изучены важные операции над множествами «объединение», «пересечение», «разность». Познакомились с новым «универсальным» множеством. Полученные знания будут необходимы при изучении темы «Отношения множеств».

Отметим следующее:

- операции объединения и пересечения коммутативны;

- операция разности не коммутативна;

-

диаграммы Венна – абстрактные круги, объединяющие все элементы множества;

- универсальное множество содержит все множества;

- доказательство теорем осуществляется на основе принадлежности элемента множества, как к левой, так и правой части;

- если элемент принадлежит множеству, то он принадлежит и объединению этого множества с любым другим множеством;

- декартовым произведением множеств называется новое множество, элементами которого являются пары, составленные из элементов исходных множеств;

- Декартова плоскость это множество .

Литература

1. Яблонский Я. В. Введение в дискретную математику. – М.: Высшая школа, 2001. - 384 с.

2. Москинова Г.И. Дискретная математика. – М.: Логос, 2002. – 240 с.

3. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Физматлит, 2001.

4. Самсонов Б.Б. и др. Компьютерная математика. – Ростов-на-Дону: Феникс, 2002. – 512 с.

5. Демидович Б.П, Кудрявцев В.А.. Краткий курс высшей математики. – М.: Наука, 2001. - 656 с.

Лекция 3

Отношения

1. Отношения на множествах, соответствия

Бинарные отношения