1. Разности:
A \ B = A \ (A  B) и A \ (B
B) и A \ (B  C)=(A \ B)
C)=(A \ B)  (A \ C).
(A \ C).
Важно!!!
Операция разности определяется только для двух множеств. Эта операция двухместная и не коммутативная:  .
.
2. Свойство симметрической разности:

 .
.
Доказательство.
Доказательство этого свойства, как и других утверждений о равенстве каких-либо множеств, состоит в том, чтобы, предположив принадлежность некоторого элемента x множеству из левой части равенства, доказать, что этот же самый элемент принадлежит множеству, стоящему в правой части равенства и наоборот.
Пусть  , что по определению симметрической разности означает, что x
, что по определению симметрической разности означает, что x  (A \ B)
(A \ B) 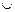 (B \A). Здесь возможны два варианта: либо x
(B \A). Здесь возможны два варианта: либо x  (A \ B), либо x
(A \ B), либо x  (B \ A). В первом случае мы получаем: x
(B \ A). В первом случае мы получаем: x  (A \ B)
(A \ B)  (x
(x  A и x
A и x  B)
B)  (x
(x  A
A  B и x
B и x  A
A  B), откуда очевидно следует, что x
B), откуда очевидно следует, что x  . Ситуация, когда x
. Ситуация, когда x  (B \ A), рассматривается аналогично.
(B \ A), рассматривается аналогично.
Итак, мы доказали, что если некоторый элемент x принадлежит множеству из левой части равенства, то из этого следует, что он принадлежит множеству, стоящему в правой части равенства. Теперь нам необходимо доказать обратное включение.
Пусть x 
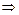 (x
(x  A
A 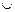 B и x
B и x  A
A  B). Здесь возможны две ситуации: либо
B). Здесь возможны две ситуации: либо 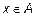 и
и  , либо
, либо  и
и 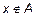 . Рассмотрим первый случай: пусть
. Рассмотрим первый случай: пусть  и
и  ,
,  . Откуда
. Откуда  .Второй случай доказывается аналогично.
.Второй случай доказывается аналогично.
Важно!!!
Итак, мы полностью доказали заявленное свойство. При доказательстве подобных утверждений огромную роль играет то свойство, что если некоторый элемент x принадлежит некоторому множеству X, то он, очевидно, будет принадлежать и объединению множества X с произвольным другим множеством.
Определение 5.
Множество U, такое, что все рассматриваемые множества являются его подмножествами, называется универсальным.
 То есть это множество, которое по предположению содержит все используемые нами множества. Обозначается не кругом, а прямоугольником (рис. 5).
То есть это множество, которое по предположению содержит все используемые нами множества. Обозначается не кругом, а прямоугольником (рис. 5).
ПРИМЕР 5.
Множества {звездные скопления}, {черные дыры}, {планеты} являются подмножествами универсального множества {вселенная}.
Определение 6.
Множество U \ A называется дополнением множества A (до универсального множества) и обозначается через 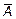 .
.
На кругах Эйлера это определение представлено на рис. 5.
Принцип двойственности
Теорема двойственности
Теорема 1 (двойственности или де-Моргана).
Пусть Ak, k = 1,..., n – некоторые подмножества универсального множества U, тогда имеют место следующие равенства:
 ;
;  . (5)
. (5)
Эти равенства, связывающие операции пересечения и объединения множеств и их дополнений до универсального множества, называют соотношениями принципа двойственности.
Доказательство.
 .
.
Заметим, что в приведенном доказательстве все утверждения об элементе x соединены знаками  , что позволяет одновременно строить доказательство утверждения в обе стороны.
, что позволяет одновременно строить доказательство утверждения в обе стороны.
ПРИМЕР 6.
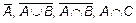 .
.
Решение.
1.
 – это множество нечетных натуральных чисел, т.е. множество B.
– это множество нечетных натуральных чисел, т.е. множество B.
2. Каждое натуральное число является либо четным, либо нечетным, поэтому 
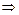
 =
=  .
.
3.  =
=  . Следовательно,
. Следовательно, 
 = N.
= N.
4. A  C = { четные натуральные числа
C = { четные натуральные числа 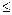 10} = {2, 4, 6, 8, 10}.
10} = {2, 4, 6, 8, 10}.
Базис операций
Если теперь считать, что в нашем распоряжении имеется универсальное множество U, то операции  ,
, 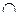 , \ и
, \ и  можно определять друг через друга и фактически ввести некоторый базис операций в алгебре множеств.
можно определять друг через друга и фактически ввести некоторый базис операций в алгебре множеств.
ПРИМЕР 7.
1.  .
.
2.  .
.
3.  .
.
Определение 7.
Операции { 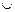 ,
,  , \} называются булевыми операциями над множествами.
, \} называются булевыми операциями над множествами.






