Үйге: №30(2), 31 (1), 32 (1), 33, 35
7-сабақ
Сабақтың тақырыбы: Ромб және оның қасиеттері
Сабақтың мақсаты:
Білімділік: Ромб анықтамасын білу, қасиетін тұжырымдайтын теореманы білу, дәлелдей білу, теоремалық білімді есеп шығару барысында қолдана білу.
Дамытушылық: Оқушылардың ойлау қабілетін,есеп шығару дағдысы мен икемділігін жетілдіру, пәнге деген қызығушылығын арттыру
Тәрбиелік: Оқушыларды оқуға, жауапкершілікке, ұқыптылыққа, өз бетінше жұмыс істеуге, қорытынды шығаруға тәрбиелеу.
Сабақ түрі: Жаңа білімді меңгерту
Сабақтың барысы: 1. Ұйымдастыру кезеңі
2. Үй тапсырмасын тексеру, сұрау
3. Жаңа сабақ түсіндіру
4. Жаңа сабақты бекіту мен жинақтау, есептер шығару
5. Қорытындылау, бағалау
6. Үйге тапсырма
ІІ. Класта өтілген тақырып бойынша сұрақ қойып қайталау.
1) Параллелограмм анықтамасы
2) Параллелограмның қасиеттері
3) Параллелограмның белгілері
4) Параллелограмның периметрін табатын формула
ІІІ. Жаңа сабақты түсіндіру:
Анықтама: Барлық қабырғалары тең параллелограмм ромб деп аталады.


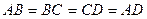
Ромб деген сөйлем параллеллограмның дербес түрі болғандықтан параллелограмның барлық қасиеттері ромбының қасиеттері болады.
Оқушыларға сұрақ қойып ромбының қасиеттерін айтқызу.
1. Ромбының қарама – қарсы бұрыштары тең
2. Ромбының бір қабырғасына іргелес бұрыштарының қосындысы 1800 қа тең.
3. Ромбының диагональдары қиылысу нүктесінде тең екіге бөлінеді
4. Ромбының диагональі оны өзара тең екі үшбұрышқа бөледі
Оқушылар енді оның қасиеттері мен бірге ромбының өзіне ғана тән мынадай қасиеті бар екен. Ол қасиеті мына теоремада тұжырымдалады.
Теорема: Ромбының диагональдары тік бұрыш жасап қиылысады. Ромбының диагональдары оның бұрыштарының биссекрисалары болады.
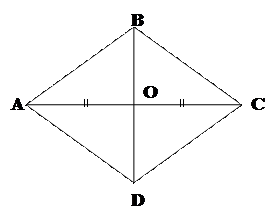
Берілгені: АВСД ромб
Дәлелдеу керек:
1. 
2. 

Дәлелдеу: 
Ромб қасиеті бойынша АВ=ВС бұдан тең бүйірлі ΔАВС үшбұрышының ВО-медианасы болып табылады, ал тең бүйірлі үшбұрыштың табанына жүргізілген медиана қасиетін еске түсірейік.
Оқушылар: Тең бүйірлі үшбұрыштың төбесінен табанына жүргізілген медиананың қасиетін айтады. Демек
ВО 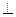 АС әрі <АВО=
АС әрі <АВО=  СВО
СВО
Осы сияқты  екені дәлелденді. Енді ромбының белгілерін тұжырымдайық.
екені дәлелденді. Енді ромбының белгілерін тұжырымдайық.
Өзіне тән қасиеттеріне кері теорема құрастырыңдар
1. Егер параллелограмның диагональдары өзара перпендикуляр болса, онда ол ромб болады.Өздері дәлелдейді
2. Егер параллелограмның диагональдары оның бұрыштарының биссектрисасы болса, онда ол ромб болады.
3. Анықтамадан шығару. Қабырғалары бір-біріне тең төртбұрыш ромб болады.
Параллелограмның биіктігінң анықтамасын сұраймын.

Енді ромбының В төбесінен түсірілген ВЕ және ВF биіктіктері туралы не айтуға болады?
Оқушылар: ΔВЕА және ΔВFС гипотенузасы мен сүйір бұрышы бойынша бұл үшбұрыштар тең екенін айтып, онда ВЕ=ВF. Ромбының биіктіктері тең
Ромб периметрі Р=4а болады.
ІҮ. Өтілген тақырыпты бекіту.
№41. (ауызша) №42 (ауызша), №43 (ауызша), №44 (ауызша)
№46. Тіктөртбұрыштың қабырғаларының орталары ромбының төбелері болатынын дәлелдеңдер.

Берілгені: АВСД тіктөртбұрыш
АК=ВК, BN=NC, CF=  , АН=
, АН= 
Дәлелдеу керек: KNFH-ромб
Дәлелдеуі: Екі катеттерінің теңдігі бойынша ΔNBK=ΔNCF=ΔHДF=ΔНАК.
Онда бұл үшбұрыштардың гипотенузалары да тең. KN=NF=FH=KH қабырғаларының теңдігі бойынша төртбұрыш KNFH-ромб болады.
 №47.
№47.
Берілгені:  ромб
ромб
<АВО-<ВАО=150
Табу керек: <АВС,  -?
-?
Шешуі: ΔАОВ- тік бұрышты үшбұрыш
<ВАО+<АВО=900
<АВО-<ВАО=150
2<АВО =1050
2<АВО=<АВС
<АВС=1050
 =1800-1050=750
=1800-1050=750
Жауабы: 750 және 1050
№49.
Берілгені: АВСД ромб
 ,
, 
Табу керек: <А, <АВС-?
Шешуі: ΔАКВ- тік бұрышты үшбұрышта 
 АК=
АК=  АВ АК – катеті гипотенузаның жартысына тең болғандықтан <АВК=300 болады, ал <А=900-<АВК=900-300=600
АВ АК – катеті гипотенузаның жартысына тең болғандықтан <АВК=300 болады, ал <А=900-<АВК=900-300=600
 бұдан
бұдан  = 1200
= 1200
Жауабы: 600 және 1200
№51.
Қабырғасы және диагоналі бойынша ромб салыңдар
Салу жолы: 2 жағдай қарастырамыз. d1= 
1. е сәулесін саламыз
2. сәуледен  =а кесіндісін өлшеп саламыз
=а кесіндісін өлшеп саламыз
3.  шеңбер саламыз, В€
шеңбер саламыз, В€  болады
болады
4. 
5. 
6.  жүргіземіз
жүргіземіз
7.  жүргіземіз
жүргіземіз
8.  деп белгілейміз.
деп белгілейміз.  ізделінді ромб.
ізделінді ромб.
Ромб екенін дәлелдейміз. Салуымыз бойынша 
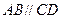 бұдан
бұдан 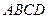 параллелограмм
параллелограмм
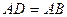 болғандықтан
болғандықтан 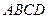 ромб
ромб

ІІ жағдай d1=АС диагональі болса
1. е сәулесін саламыз
2. сәуледен  =а кесіндісін өлшеп саламыз
=а кесіндісін өлшеп саламыз
3.  шеңбер саламыз, С€
шеңбер саламыз, С€ 
4. 
5. 
6.  жүргіземіз
жүргіземіз
7. 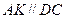 жүргіземіз
жүргіземіз
8. 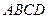 ізделінді ромб
ізделінді ромб

Ү. Қорытындылап, бағалау
ҮІ. Үйге тапсырма: №48, 50, 51 (2)
8-сабақ
Сабақтың тақырыбы: Квадрат
Сабақтың мақсаты:
Білімділік: Квадраттың анықтамасын және қасиеттерін білу. Тіктөртбұрыш пен квадраттың, ромб пен квадраттың ортақ қасиеттерін және айырмашылығын білу, қасиеттерін есеп шығару барысында қолдана білу.
Дамытушылық: Оқушыларды сызбамен жұмыс істеу қабілеттері мен дағдыларын дамыту.
Тәрбиелік: Оқушыларды шапшаңдыққа, ұқыптылыққа баулу
Сабақ түрі: Жаңа сабақты меңгерту
Сабақтың барысы: 1. Ұйымдастыру кезеңі
2. Үй тапсырмасын тексеру, сұрау
3. Жаңа сабақ түсіндіру
4. Бекіту, есептер шығару
5. Қорытындылау, бағалау
6. Үйге тапсырма
2. Үй тапсырмасын тексеру, сұрау
Интерактивті тақтадан дайын сызбалар бойынша есептер шығару.
| 1. |

| Берілгені: 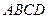 ромб ромб
 А=500
Табу керек: А=500
Табу керек:  -? -?
|
| 2. |

| Берілгені: 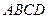 ромб ромб
 =750
Табу керек: =750
Табу керек:  АВС-? АВС-?
|
| 3. |
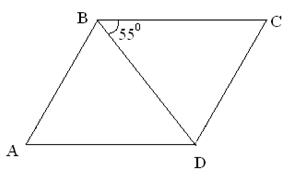
| Берілгені:  ромб ромб
 =550
Табу керек: =550
Табу керек:  -? -?
|
| 4. |

| Берілгені:  ромб ромб

 =200
Табу керек: =200
Табу керек:  -? -?
|
| 5. |
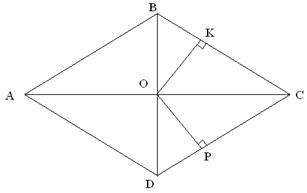
| Берілгені: 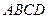 ромб ромб
 =О
ОК =О
ОК 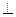 ВС, ОР ВС, ОР 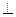  Д/к: ОК=ОР
Д/к: ОК=ОР
|
ІІІ. Жаңа сабақты меңгерту.
|



Анықтама:
1. Барлық қабырғалары тең тік ромб квадрат деп аталады.
Бұдан тіктөртбұрыш пен ромбының барлық қасиеттері квадрат үшін орындалады.
Оқушылардан сұраймын.
1. Квадраттың диагональдары тең болады
2. Квадраттың диагональдары қиылысу нүктсінде тең екіге бөлінеді.
3. Квадраттың диагональдары тік бұрыш жасап қиылысады.
4. Квадратты диагональдары оның бұрыштарының биссектрисалары болады.
Квадраттың периметрі: Р=4а
№52 ауызша, №53 ауызша
В С
 №54.
№54.
Берілгені: АВСD ромб
АС=ВD
Дәлелдеу керек: АВСD квадрат
А D
Дәлелдеуі: <А=<В=900 екенін дәлелдеу керек. АВСD ромб болғандықтан ВD 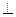 АС, ВО=ОD, ОА=ОС, ал шарт бойынша АС=ВD ендеше ВО=АО, демек ΔАОВ- тең бүйірлі тік бұрышты үшбұрыш, онда <ВАО=<АВО=450
АС, ВО=ОD, ОА=ОС, ал шарт бойынша АС=ВD ендеше ВО=АО, демек ΔАОВ- тең бүйірлі тік бұрышты үшбұрыш, онда <ВАО=<АВО=450
Ал, <ВАD=2<ВАО=900
<АВС=2<АВО=900 дәлелденді
№56. Егер квадраттың қабырғасы 4,5 см-ге ұзарса, онда берілген квадраттың периметрі қалай өзгереді?
Шешуі: Берілген квадраттың қабырғасы а десек
Р=4а а1=а+4,5
Р1=4а1
Р1=4(а+4,5) =4а+18=Р+18
Р1=Р+18
Жауабы: 18 см ұзарады
4) 2 есе қысқарса ше
Р=4а а1=  а
а
Р1=4а1=4∙  а=
а=  ∙4а=
∙4а=  Р
Р
Р1=  Р
Р
Жауабы: периметрі екі есе қысқарады.
Қосымша есептер
Дайын сызбадан көрсетіледі.
| 1. |

| Берілгені: АВСD-квадрат ВВ1 =СС1=DD1=АА1 Дәлелдеу керек: А1B1C1D1-квадрат екенін |
| 2. |

| Берілгені: АВСD-квадрат
 Дәлелдеу керек:
Дәлелдеу керек:  - ромб екенін - ромб екенін
|
| 3. |

| Берілгені: АВСD-квадрат
ВВ1=ВА1=D1C1=DD1
Дәлелдеу керек:
 тіктөртбұрыш тіктөртбұрыш
|






