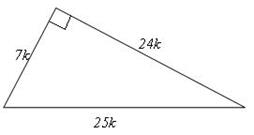
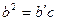Бізге тікбұрышты үшбұрыш, оның катеттері мен гипотенузасы, сүйір бұрыштары ұғымдары белгілі. Бүгінгі сабақта тікбұрышты үшбұрыштың қабырғалары мен бұрыштарының арасындағы байланысты қарастырамыз.

АВС тікбұрышты үшбұрыш берілген
(27-сурет). Оның катеттері а, b ал гипотенузасы с деп, бір сүйір бұрышын мысалы  А=α деп белгілейік.
А=α деп белгілейік.  С=90º болсын.
С=90º болсын.
27-сурет
Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің гипотенузаға қатынасы сол бұрыштың косинусы деп аталады. Оны қысқаша cosα=  (1) түрінде жазады. (1) қатынас α бұрышының шамасына ғана тәуелді, қабырғалардың ұзындықтарына тәуелді емес.
(1) түрінде жазады. (1) қатынас α бұрышының шамасына ғана тәуелді, қабырғалардың ұзындықтарына тәуелді емес.
20-теорема. Бұрыштың косинусы мен тек оның градустың өлшеміне ғана тәуелді.
Дәлелдеу: АВС тікбұрышты үшбұрышы берілсін. Бұл үшбұрыш үшін (1) теңдік орындалсын.

 АВ сәулесіне AD=к.с кесіндісін (28-сурет). Ал АС сәулесіне АЕ=к.в (к-оң сан) өлшеп саламыз. Мұндағы, ΔADE –тікбұрышты үшбұрыш және cosα=
АВ сәулесіне AD=к.с кесіндісін (28-сурет). Ал АС сәулесіне АЕ=к.в (к-оң сан) өлшеп саламыз. Мұндағы, ΔADE –тікбұрышты үшбұрыш және cosα=  екенін дәлелдейміз. Шынында
екенін дәлелдейміз. Шынында 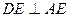 болады. Керісінше ұйғарып, DE кесіндісін АЕ түзуіне перпендикуляр емес делік. Сонда D нүктесінен АЕ түзуіне DF перпендикулярын түсіруге болады. Нәтижесінде, ADF тікбұрышты үшбұрышы үшін cosα=
болады. Керісінше ұйғарып, DE кесіндісін АЕ түзуіне перпендикуляр емес делік. Сонда D нүктесінен АЕ түзуіне DF перпендикулярын түсіруге болады. Нәтижесінде, ADF тікбұрышты үшбұрышы үшін cosα= 
қатынасын жазамыз. Ал (1) теңдіктің негізінде  аламыз, бірақ
аламыз, бірақ  немесе
немесе 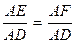 болып қалады. Онда AE=AF және cosα=
болып қалады. Онда AE=AF және cosα=  шығады. Теорема дәлелденді.
шығады. Теорема дәлелденді.
Анықтама. Тікбұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің гипотенузаға қатынасы сол бұрыштың синусы деп аталады да,
 (2)
(2)
түрінде жазылады.
Анықтама. Тікбұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің іргелес жатқан катетке қатынасы сол бұрыштың тангенсі деп аталады. Оны
 (3)
(3)
түрінде жазады.
Анықтама. Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің қарсы жатқан катетке қатынасы сол бұрыштың катангенсі деп аталады. Оны
 (4)
(4)
түрінде жазамыз.
sinα, cosα, tgα және ctgα-ларды тригонометриялық өрнектер деп атайды.
Мысалы. Сүйір бұрышының косинусы 3:56 қатынасына тең болатын үшбұрышты салайық.
Шешуі: Ізделінді тікбұрышты үшбұрыш АВС болсын, мұндағы АВ=c-гипотенуза; <С=900; <A=α, BC=a, CA=b-катеттер.
cosα=  теңдігі орындалу керек. Бірлік кесінді е таңдап аламыз.
теңдігі орындалу керек. Бірлік кесінді е таңдап аламыз.  сәулелерін жүргіземіз. 29 –сурет.
сәулелерін жүргіземіз. 29 –сурет.

СЕ сәулесіне СА=3е кесіндісін өлшеп саламыз. Центрі А нүктесі етіп, АВ=5a кесіндісіне тең радиус етіп шеңбер жүргіземіз. Ол CF сәулесін В нүктесінде қиып өтеді. Нәтижесінде АВС тікбұрышты үшбұрышы салынады. Ол тікбұрышты үшбұрышта
cosα= 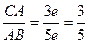 болады. Демек, салынған үшбұрыш есептің шартын қанағаттандырады.
болады. Демек, салынған үшбұрыш есептің шартын қанағаттандырады.
Есептер шығару.
№118. Сүйір бұрыштың синусы 1)  ; 3) 0,6-ға тең тікбұрышты үшбұрыш салыңдар.
; 3) 0,6-ға тең тікбұрышты үшбұрыш салыңдар.
Шешуі:

Берілгені:  СЕ сәулесіне СВ=1 бірлік кесіндіні өлшеп СВ=a=1 саламыз. Центрі В, радиусы 2-ге тең шеңбер саламыз, ол CF түзуін А нүктесінде қиып өтеді. АВС үшбұрышы есеп шартын қанағаттандырады.
СЕ сәулесіне СВ=1 бірлік кесіндіні өлшеп СВ=a=1 саламыз. Центрі В, радиусы 2-ге тең шеңбер саламыз, ол CF түзуін А нүктесінде қиып өтеді. АВС үшбұрышы есеп шартын қанағаттандырады.
3)
 sinα=0.6
sinα=0.6

№120. Сүйір бұрыштың тангенсі 1)  ; 3) 1-ге тең тікбұрышты үшбұрыш салыңдар.
; 3) 1-ге тең тікбұрышты үшбұрыш салыңдар.
 1)
1)  ,
, 
Шешуі:  түзулерін жүргізіп, СЕ сәулесінің бойына СА=3, ал CF сәулесінің бойына СВ=2 кесінділерін өлшеп саламыз. АВС - ізделінді үшбұрыш.
түзулерін жүргізіп, СЕ сәулесінің бойына СА=3, ал CF сәулесінің бойына СВ=2 кесінділерін өлшеп саламыз. АВС - ізделінді үшбұрыш.

3) tgα=1,  да а=b екені белгілі болып отыр.
да а=b екені белгілі болып отыр.
Орытындылау (слайд)
 cosα=
cosα= 


Слайд бойынша ережелерді қайталау.
5. Үйге: §8. №118(2), №119(2), №120 (2), 121 (2)
24-сабақ
Сабақтың тақырыбы: Есептер шығару
Сабақтың мақсаты:
Білімділік: Тікбұрыты үшбұрыштың сүйір бұрышының синусының, косинусының, тангенсінің, котангенсінің анықтамаларын есептер шығаруда қолдану.
Дамытушылық: Оқушылардың өз бетінше ой қорыта білу және математика тілінде сөйлеу дағдыларын қалыптастыру.
Тәрбиелік: Оқушыларды өзара бір-біріне көмек беруге үйрету және адамгершілікке тәрбиелеу.
Сабақ түрі: Практикалық сабақ
Көрнекілігі: Сызбалар, интерактивті тақта, слайд, карточкалар, сызғыш
Сабақтың барысы: 1. Ұйымдастыру кезеңі
2. Үй тапсырмасын сұрау
Сұрақтар. 1. Неліктен тікбұрышты үшбұрыштың синусының, косинусының, тангенсінің, котангенсінің мәндері үшбұрыштың қабырғаларының ұзындықтарына тәуелді болмай, тек сүйір бұрышының шамасына тәуелді болады? Жауапты түсіндір?
2.  мен
мен  - ны өзара кері өрнектер деп айтуға бола ма? Жауапты түсіндір.
- ны өзара кері өрнектер деп айтуға бола ма? Жауапты түсіндір.
№118. 2) Сүйір бұрыштың синусы 2:5 қатынасына тең тікбұрышты үшбұрыш салыңдар.
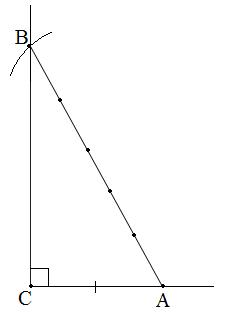
Шешуі: 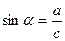 яғни
яғни 
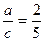 , a=2, b=5
, a=2, b=5
Жауабы: ∆АВС – ізделінді үшбұрыш.
№119. 2) Сүйір бұрыштың косинусы 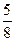 - қатынасына тең тікбұрышты үшбұрыш салыңдар.
- қатынасына тең тікбұрышты үшбұрыш салыңдар.

Шешуі: 

 , b=5, c=8
, b=5, c=8
Жауабы: ∆ВС –Ізделінді үшбұрыш
№120. 2) Сүйір бұрыштың тангенсі  -ке тең тікбұрышты үшбұрыш салыңдар
-ке тең тікбұрышты үшбұрыш салыңдар

Шешуі:

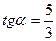 a=5, b=3
a=5, b=3
∆АВС ізделінді үшбұрыш
 №121. 2) Сүйір бұрыштың котангенсі 1,5 – ке тең тікбұрышты үшбұрыш салыңдар.
№121. 2) Сүйір бұрыштың котангенсі 1,5 – ке тең тікбұрышты үшбұрыш салыңдар.
Шешуі:
 ,
,  ,5
,5  , а=2, b=3
, а=2, b=3
(Күннің ретін жазу)
Есептер шығару.
Оқулықпен жұмыс
№»123
Егер теңбүйірлі үшбұрыштың бүйір жағы 5дм табыны, ал биіктігі 4 дм болса, табанындағы бұрыштың 1) косинусын; 3) тангенсін табыңдар.

Шешуі:
∆АВС: АВ=BC=5 дм
АС =6 дм, 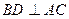
BD=4 дм. <А=<C
1)  , ∆ABD: AB =
, ∆ABD: AB = 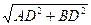 =
=  =
= 

3) 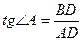 , AD=
, AD=  ,
, 
Жауабы: 1) 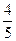 ; 3)
; 3) 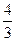
№125
1) BC=8, AB=17, AC=15; 3) BC=1, AC=2, AB= 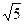 болса, С бұрышы тік болатын үшбұрыштың А және В сүйір бұрыштарының синусы мен косинусын табыңдар.
болса, С бұрышы тік болатын үшбұрыштың А және В сүйір бұрыштарының синусы мен косинусын табыңдар.
Шешуі: ∆АВС,  , sinα-? cosα-? sinβ-? cosβ-?
, sinα-? cosα-? sinβ-? cosβ-?
1) sinα= 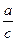 , a=BC=8, c=AB=17,
, a=BC=8, c=AB=17, 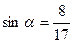 .
.
 , b=AB=15, c=AB=17,
, b=AB=15, c=AB=17, 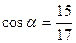 ,
,
sinβ=  , b=AC=15, c=AB=17, sinβ=
, b=AC=15, c=AB=17, sinβ=  =
= 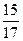
 , a=BC=8, c=AB=17, cosβ=
, a=BC=8, c=AB=17, cosβ= 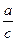 =
= 
3) sinα= 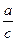 , a=BC=1, c=AB=
, a=BC=1, c=AB= 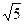 ,
,  .
.
 , b=AB=2, c=AB=
, b=AB=2, c=AB= 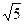 ,
, 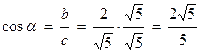 ,
,
sinβ=  , b=AC=2, c=AB=
, b=AC=2, c=AB= 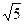 , sinβ=
, sinβ=  =
= 
 , a=BC=1, c=AB=
, a=BC=1, c=AB= 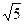 , cosβ=
, cosβ= 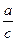 =
= 
Жауабы: 1) 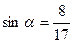 ,
, 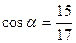 , sinβ=
, sinβ= 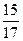 , cosβ=
, cosβ= 
2)  ,
,  , sinβ=
, sinβ=  , cosβ=
, cosβ= 
1 карточка.
Берілгені: ∆АВС, <С=900
α- сүйір бұрышы
с-гипотенуза
Т/К: β, а, в -?
Шешуі: 
β=900-α. 
2 карточка.
Берілгені: ∆АВС, <С=900
a,b –катеттері
Т/Кα, β (а мен в арқылы
Шешуі:  ;
; 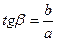
Қорытындылау:

Шешуі: ∆АВС, АВ=BC=в
 А=
А=  C=α
C=α
AC  жүргіземіз
жүргіземіз
S∆=  AC∙BD
AC∙BD
∆ABD:sinα= 
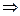 BD=ABsinα=bsinα∙cosα=
BD=ABsinα=bsinα∙cosα= 
AC=2∙AD=2∙bcosα
S= 
Үйге: №23(2,4), 25 (2,4)

25-сабақ
Сабақтың тақырыбы: Тест жұмысы
Сабақтың мақсаты:
Білімділік: Оқушылардың білімін тексеріп, бағалау
Дамытушылық: Оқушылардың өз бетінше ізденіп, логикалық ойлауын қалыптастыру
Тәрбиелік: Оқушыларды ұқыптылыққа, ізденімпаздыққа және уақытты тиімді пайдалануға үйрету.
Сабақ түрі: Пысықтау
Көрнекілігі: Тест, интерактивті тақта
Сабақтың барысы: 1. Ұйымдастыру кезеңі
2. Тест тапсырмаларын орындау
Тест
А
1. Тікбұрышты үшбұрыштың қарсы жатқан катетінің гипотенузаға қатынасы: 5:10. Тікбұрышты үшбұрыштың сүйір бұрышының синусы неге тең?
А.  В. 2 C.
В. 2 C. 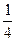 D.
D.  Е. 1
Е. 1
2. Тікбұрышты үшбұрыштың іргелес жатқан катетінің гипотенузаға қатынасы: 4:4. Тікбұрышты үшбұрыштың сүйір бұрышының косинусы неге тең?
А. 2 В.  С.1 D.0 E.4
С.1 D.0 E.4
3. Тікбұрышты үшбұрыштың катеттерінің қатынасы:  . Сүйір бұрыштың тангенсі неге тең?
. Сүйір бұрыштың тангенсі неге тең?
А. 0 B.  C.
C. 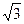 D.
D.  E. 2
E. 2
4. Тәкбұрышты үшбұрыштың катеттерінің қатынасы:  . Тікбұрышты үшбұрыштың сүйір бұрышының катангенсі неге тең?
. Тікбұрышты үшбұрыштың сүйір бұрышының катангенсі неге тең?
A. 1 B. 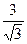 C.
C.  D.
D. 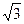 E. 3
E. 3
5. Тікбұрышты үшбұрыштың бір катеті 3 см және іргелес жатқан бұрыштың косинусы  -ге тең. Үшбұрыштың гипотенузасын табыңдар.
-ге тең. Үшбұрыштың гипотенузасын табыңдар.
А. 3см В. 2см С. 1см D.5 cм E. 6 см
6. Тікбұрышты үшбұрыштың бір катеті 2 см және іргелес жатқан бұрыштың синусы  -ге тең. Үшбұрыштың екінші катетін табыңдар.
-ге тең. Үшбұрыштың екінші катетін табыңдар.
А. 2см В. 5см С. 3см D.1 cм E. 6 см
7. Биіктігі 9 см теңқабырғалы үшбұрышқа іштей сызылған шеңбердің радиусын табыңдар.
А. 5 см В. 3 см С. 4 см D.10 cм E. 12 см
8. Теңбүйірлі үшбұрыштың төбесіне қатысты бұрышы 1200, ал табанына жүргізілген биіктігі 8 см. Үшбұрыштың бүйір қабырғаларын табыңдар.
А. 10 см В. 5 см С. 16 см D.12 cм E. 9 см
9. Теңбүйірлі үшбұрыштың бүйір қабырғасы 2 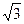 , ал төбесіне қатысты бұрышы 600 болса, оған сырттай сызылған шеңбердің радиусы неге тең?
, ал төбесіне қатысты бұрышы 600 болса, оған сырттай сызылған шеңбердің радиусы неге тең?
А. 9 см В. 6 см С. 7 см D.3 cм E. 5 см
Үйге: §8 қайталау
26 – сабақ
Сабақтың тақырыбы: Пифагор теоремасы (1-сабағы)
Сабақтың мақсаты:
1. Білімділік: Пифагор теоремасын және оған кері теореманы тұжырымдап, дәлелдеу және оларды есептер шығаруда қолдана білу
2. Дамытушылық: Тікбұрышты үшбұрыштың қабырғалары мен бұрыштары арасындағы байланыс туралы білімдерін олардың қабырғалары арасындағы байланысқа ұласатындығына көз жеткізіп, білімдерін кеңейту
3. Тәрбиелік: Ұқыптылыққа, тиянақтылыққа, мұқияттылыққа зер салу.
Сабақтың көрнекілігі: Интерактивті тақта (флипчарт, слайдтар, магнитті картолар, шаршылар, Пифагордың портреті).
Сабақтың барысы: I. Ұйымдастыру кезеңі
II. Жаңа сабақты баяндау. (Пифагор теоремасы)
Пифагордың портреті.
Гректің оқымыстысы Пифагор (б.э.д. 580-500 ж.ж.) тікбұрышты үшбұрыштың қабырғаларының арасындағы қатынасты өрнектейтін теореманы ашқан. Пифагор теоремасы және оған кері теореманы өз бетімізбен ізденіп, тұжырымдап және оны ізденіс үстінде дәлелдейтін боламыз. Ол үшін «Не? Қандай? Қалай?» іздену, қимыл-жауап ойынын ойнаймыз.
Алдарыңыздағы фигураларға назар аударыңыздар (оқушылардың парталарында жеке-жеке үш шаршыдан және тақтада магнитті түрде көрсетіледі).
- Бұл қандай фигуралар? (шаршылар)
- Оның өлшемі нені білдіреді? (аудан)
- Шаршы аудандарының арасында қандай байланыс бар? (кішілерінің қосындысы үлкеніне тең)
- Әрбір екеуінің тек бір ғана ортақ төбесі болатындай етіп орналастыруға бола ма? (уақыт беріледі)
- Қандай фигура пайда болды? (үшбұрыш)
- Үшбұрыштың қай түрі? (тікбұрышты үшбұрыш)
- Үшбұрыш пен шаршылардың қандай элементтері арасында байланыс бар? (қабырғалары сәйкес)
- Қандай қорытындыға келуге болады? (катеттер квадраттарының қосындысы гипотенузаның квадратына тең)
Дұрыс, міне осылайша кітаптағы 42 беттетгі 21-теореманың тұжырымдамасын сұрақтарға жауап бере отырып таптық(Тақтада магнитті шаршылардан да құрастырылды).
Теорема. Тікбұрышты үшбұрыштың гипотенузасының квадраты катеттерінің квадраттарының қосындысына тең (экранда слайд).

Пифагор теоремасы 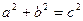
Осы тұжырымды дәлелдеуге назар аударалық. 2-слайд, 3-слайд, 4-слайд, 5-слайд, 6-слайд бірінен-соң бірі көрсетіледі де, ойланып ой қорытындысын айтуға 5 минут уақыт беріледі.

Жауап: Тікбұрышты үшбұрыштың тік бұрышынан гипотенузаға биіктік жүргізіледі, үшбұрыштар тік бұрышты.

|
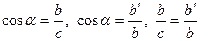

Жауап: Сүйір бұрышы ортақ тікбұрышты үшбұрыштар. Тік бұрыштардағы сүйір бұрыштардың косинустарын анықтайды. Теңдіктердің оң жақ бөліктерін теңестіреді. Пропорцияның негізгі қасиетінен катеттің квадраты гипотенуза мен катеттің гипотенузадағы проекциясы арқылы өрнектеледі.
|


Жауап: Осындай жолмен екінші катетті гипотенуза мен оның гипотенузадағы екінші проекциясы арқылы өрнектелген өрнекті анықтайды.

|


Жауап: 3-слайд пен 4-слайд қорытындыларын мүшелеп қосады. Нәтижесінде катеттердің проекцияларының қосындысы гипотенузаның ұзындығына тең екендігі шығады.

Жауап: Тікбұрышты үшбұрыштың катеттерінің квадраттарының қосындысы гипотенузаның квадратына тең.
(Теорема тұжырымдамасы мен формуласы оқушы дәптеріне түседі.)
Енді осы теоремаға кері теореманы практикалық жолмен дәлелдеуімізді еске түсірейік. Сонымен, үшбұрыштың бір қабырғасының квадраты қалған екі қабырғасының квадраттарының қосындысына тең болса, онда үшбұрыш тікбұрышты үшбұрыш болады.
7-слайд (Арнайы тікбұрышты үшбұрыштар арқылы қорытынды шығарады)