Закон сохранения механической энергии

Вопрос 1

1. Механическое движение, его виды. Основная задача механики. Радиус – вектор, перемещение. Уравнение движения. Равномерное движение. Скорость равномерного движения, зависимость координаты от времени при равномерном движении.

 

Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени.Рассмотрение любого движения начинают с выбора системы отсчета, включающей в себя: тело отсчета, систему координат и приборы для исследования движения.

Основные виды механического движения.

Поступательное движение – это движение тела, при котором все его точки движутся одинаково.

Например, автомобиль совершает по дороге поступательное движение. Точнее, поступательное движение совершает только кузов автомобиля, в то время как его колёса совершают вращательное движение.

Вращательное движение – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось.

Колёса совершают вращательное движение вокруг своих осей, и в то же время колёса совершают поступательное движение вместе с кузовом автомобиля. То есть относительно оси колесо совершает вращательное движение, а относительно дороги – поступательное.

Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях.

Например, колебательное движение совершает маятник в часах.

Поступательное и вращательное движения – самые простые виды механического движения.

Основная задача механики— определять положение (координаты) движущегося тела в любой момент времени.

Материальная точка - модель тела, размерами которого в рассматриваемых условиях можно пренебречь.

Траектория - линия, вдоль которой движется тело.

Путь - длина траектории.

Перемещение - вектор, соединяющий начальное и конечное положения тела.

Ра́диус-ве́ктор (обычно обозначается или просто) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Равномерным движением называют такое движение, при котором тело за любые одинаковые промежутки времени проходит одинаковые пути. Примерами равномерного движения, являются движения тел, которые тонут в воде, движение парашютиста после раскрытия парашюта, движение воздушного пузырька в стеклянной трубке, заполненной водой, движение стрелки часов.

Скоростью равномерного, прямолинейного движения тела называют величину, равную отношению перемещения тела к промежутку времени, в течение которого это перемещение произошло.

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x0 + vt.

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x0 – vt.

Вопрос 2:

2. Неравномерное движение. Средняя скорость и средняя путевая скорость. Мгновенная скорость при неравномерном движении. Решение основной задачи механики для неравномерного движения.

 

Движение, при котором за равные промежутки времени тело совершает неравные перемещения называют неравномерным или переменным. Средней скоростью vср называется величина, равная отношению перемещения тела ∆r за некоторый промежуток времени ∆t к этому промежутку:

Модуль средней скорости определяется как отношение пути ∆S, пройденного телом за некоторый промежуток времени, к этому промежутку:

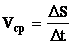
Направление вектора средней скорости vср совпадает с направлением ∆r.

При неограниченном уменьшении ∆t, vср стремится к предельному значению, которое называется мгновенной скоростью. Итак, мгновенная скорость v есть предел, к которому стремится средняя скорость vср, когда промежуток времени движения стремится к нулю:

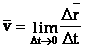
Средняя путевая скорость равна отношению полного пути к промежутку времени, за который этот путь пройден.

 

 

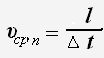
Мгновенная скорость v есть векторная величина, равная первой производной радиуса - вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения.

Вопрос 3:

3. Равноускоренное движение. Ускорение при равноускоренном движении. Зависимость скорости и координаты тела от времени при равноускоренном движении. Мгновенное ускорение при неравномерном движении.

 

Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению.

Примером такого движения является движение тела, брошенного под углом к горизонту в однородном поле силы тяжести — тело движется с постоянным ускорением, направленным вертикально вниз.

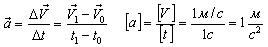
Это отношение называют ускорением. Ускорение характеризует быстроту изменения скорости.

Ускорением тела при равноускоренном движении называют векторную физическую величину, равную отношению изменении скорости тела к промежутку времени, за который это изменение произошло.

За единицу ускорения принимают ускорение такого равноускоренного движения, при котором скорость тела за 1 с изменяется на 1м/с.

Направление вектора ускорения:

а>0 (положительное ускорение) если V>Vo, и a<0 (отрицательное ускорение) если V<Vo.

Мгновенное ускорение- это ускорение тела в данный момент времени.

 

Вопрос4:

 

4. Кинематика вращательного движения. Линейные характеристики движения - длина дуги, линейная скоростью, нормальное, тангенциальное, полное ускорение.

 

Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой – оси вращения.

Кинетическая энергия вращательного движения

где Iz — момент инерции тела относительно оси вращения. 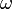— угловая скорость

Линейная скорость точки, находящейся на расстоянии R от оси вращения

,

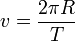Тангенциальная составляющая ускорения a_τ=dv/dt, v = ωR и

Нормальная составляющая ускорения

 

Тангенциальное и угловое ускорения связаны между собой соотношением at = e·R.

Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а_τ, нормальное ускорение а_n) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами:

s = Rφ, v = Rω, а_τ = R?, a_n = ω²R.

В случае равнопеременного движения точки по окружности (ω=const)

ω = ω₀ ±?t, φ = ω₀t ±?t²/2,

Вопрос 5:

5. Кинематика вращательного движения. Угловые характеристики движения - угол поворота радиус – вектора, угловая скорость, угловое ускорение.

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

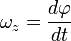
Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ. Размерность угловой скорости dim ω = Т-1, а ее единица — радиан в секунду (рад/с).

Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно:

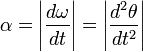
Вектор углового ускорения 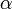направлен вдоль оси вращения (в сторону при ускоренном вращении и противоположно — при замедленном).

При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости 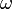по времени, то есть

Вопрос 6:

6. Законы динамики Ньютона. Сила. Масса тела. Инерциальные системы отсчета.

 

Первый закон Ньютона. В качестве первого закона Ньютон взял закон инерции Г. Галилея, который был сформулирован и обоснован нами ранее: существуют инерциальные системы отсчета, т. е. такие системы отсчета, в которых тело движется равномерно и прямолинейно, если другие тела на него не действуют. Основная роль этого закона − подчеркнуть, что в этих системах отсчета все ускорения, приобретаемые телами, являются следствиями взаимодействий тел. Дальнейшее описание движения следует проводить только в инерциальных системах отсчета.

Второй закон Ньютона утверждает, что причина ускорения тела − взаимодействие тел, характеристикой которого является сила. Этот закон дает основное уравнение динамики, позволяющее, в принципе, находить закон движения тела, если известны силы, действующие на него. Этот закон может быть сформулирован следующим образом ускорение точечного тела (материальной точки) прямо пропорционально сумме сил, действующих на тело, и обратно пропорционально массе тела:

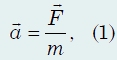здесь F − результирующая сила, то есть векторная сумма всех сил, действующих на тело.

На первый взгляд, уравнение (1) является другой формой записи определения силы, данного в предыдущем разделе. Однако это не совсем так. Во-первых, закон Ньютона утверждает, что в уравнение (1) входит сумма всех сил, действующих на тело, чего нет в определении силы. Во-вторых, второй закон Ньютона однозначно подчеркивает, что сила является причиной ускорения тела, а не наоборот.

Третий закон Ньютона подчеркивает, что причиной ускорения является взаимное действие тел друг на друга. Поэтому силы, действующие на взаимодействующие тела, являются характеристиками одного и того же взаимодействия. С этой точки зрения нет ничего удивительного в третьем законе Ньютона

точечные тела (материальные точки) взаимодействуют с силами, равными по величине и противоположными по направлению и направленными вдоль прямой, соединяющей эти тела:

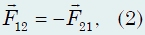где F12 − сила, действующая на первое тело со стороны

второго, a F21 − сила, действующая на второе тело со стороны первого. Очевидно, что эти силы имеют одинаковую природу. Этот закон также является обобщением многочисленных экспериментальных фактов. Обратим внимание, что фактически именно этот закон является основой определения массы тел, данного в предыдущем разделе.

 Сформулированные законы динамики играют роль своеобразных аксиом, то есть утверждений, не выводимых из более общих физических законов. Обратите внимание, что рассматриваемые законы сформулированы для точечных тел (материальных точек). Их применение для реальных тел, имеющих конечные размеры, требует уточнения и обоснования.

Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций.Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы.

Масса тела. Свойство тела, от которого зависит его ускорение при взаимодействии с другими телами, называется инертностью.

Количественной мерой инертности тела является масса тела. Чем большей массой обладает тело, тем меньшее ускорение оно получает при взаимодействии.

Поэтому в физике принято, что отношение масс взаимодействующих тел равно обратному отношению модулей ускорений:

Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив закон инерции: все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике:

Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным.

Вопрос 7:

7. Импульс тела. Закон сохранения импульса. Второй закон Ньютона в импульсной форме.

 

И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:

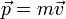
В более общем виде, справедливом также и в релятивистской механике, определение имеет вид:

Импульс — это аддитивный интеграл движения механической системы, связанный согласно теореме Нётер с фундаментальной симметрией — однородностью пространства.

Закон сохранения импульса формулируется так:

если сумма внешних сил, действующих на тела системы, равна нулю, то импульс системы сохраняется.

Тела могут только обмениваться импульсами, суммарное же значение импульса не изменяется. Надо только помнить, что сохраняется векторная сумма импульсов, а не сумма их модулей.

Как видно из проделанного нами вывода, закон сохранения импульса является следствием второго и третьего законов Ньютона. Система тел, на которую не действуют внешние силы, называется замкнутой или изолированной. В замкнутой системе тел импульс сохраняется. Но область применения закона сохранения импульса шире: если даже на тела системы действуют внешние силы, но их сумма равна нулю, импульс системы все равно сохраняется.

 

Вопрос 8:

8. Реактивное движение. Движение тела переменной массы. Уравнение Мещерского, формула Циолковского. Многоступенчатая ракета.

 

Под реактивным понимают движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно тела. При этом возникает т.н. реактивная сила, сообщающая телу ускорение.

К. Э. Циолковский вывел формулу, позволяющую рассчитать максимальную скорость, которую может развить ракета. Вот эта формула:

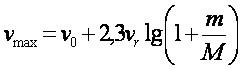
Здесь vmax – максимальная скорость ракеты, v0 – начальная скорость, vr – скорость истечения газов из сопла, m – начальная масса топлива, а M – масса пустой ракеты. Как видно из формулы, эта максимально достижимая скорость зависит в первую очередь от скорости истечения газов из сопла, которая в свою очередь зависит прежде всего от вида топлива и температуры газовой струи. Чем выше температура, тем больше скорость. Значит, для ракеты нужно подбирать самое калорийное топливо, дающее наибольшее количество теплоты. Из формулы следует также, что эта скорость зависит и от начальной и конечной массой ракеты, т.е. от того, какая часть её веса при­ходится на горючее, и какая - на бесполезные (с точки зрения скорости полёта) конструкции: корпус, механизмы, и т.д.

Эта формула Циолковского является фундаментом, на котором зиждется весь расчёт современных ракет. Отношение массы топлива к массе ракеты в конце работы двигателя(т.е. по существу к весу пустой ракеты) называется числом Циолковского.

Основной вывод из этой формулы состоит в том, что в безвоздушном пространстве ракета разовьёт тем большую скорость, чем больше ско­рость истечения газов и чем больше число Циолковского. Более двух тысяч лет назад китайцы изобрели и применили для военных целей ракеты простейшего устройства. По-видимому, китайская ракета была сходна с теми ракетами, которые применяются сейчас для фейерверка и сигнализации. Китайцы использовали свою ракету как зажигательное средство главным образом при осаде вражеских городов. Ракетная трубка с небольшим запасом пороха привязывалась к стреле. Выбрасывая такую стрелу из лука, китайские воины сообщали ракете большую начальную скорость и увеличивали дальность ее полета.

Уравнение Мещерского — основное уравнение в механике тел переменной массы, полученное И. В. Мещерским для материальной точки переменной массы (состава)

Уравнение обычно записывается в следующем виде:

,

где:

· m — масса материальной точки переменной массы, меняющаяся за счет обмена частицами с окружающей средой;

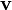· — скорость движения материальной точки переменной массы;

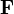· — внешние силы, действующие на материальную точку переменной массы со стороны ее внешнего окружения (в том числе, если такое имеет место, и со стороны среды с которой она обменивается частицами, например, электромагнитные силы — в случае массообмена с магнитной средой, сопротивление среды движению и т. п.);

· — относительная скорость присоединяющихся частиц;

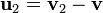· — относительная скорость отделяющихся частиц;

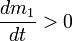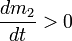· , — скорости массообмена присоединяющихся и отделяющихся частиц

переменной массы

 

В некоторых случаях тел связано с изменением их массы, например масса ракеты уменьшается вследствие истечения газов, образующихся при сгорании топлива, и т. п.

Произведем вывод уравнения движения тела переменной массы на примере движения ракеты. Если в момент времени t масса ракеты m, а ее скорость v, то по истечении времени dt ее масса уменьшится на dm и станет равной т-dm, а скорость станет равной v+dv. Изменение импульса системы за промежуток времени dt

где u - скорость истечения газов относительно ракеты. Тогда

здесь учтено, что dmdv - малое высшего порядка малости по сравнению с остальными слагаемыми. Если на систему действуют внешние силы, то dp=Fdt, поэтому

или

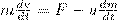(1)

Второе слагаемое в правой части (1) называют реактивной силой F_p. Если u противоположен v по направлению, то ракета ускоряется, а если совпадает с v, то тормозится.

Таким образом, мы получили уравнение движения тела переменной массы

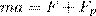(2)

которое впервые было выведено И. В. Мещерским (1859-1935).

Многоступе́нчатая раке́та — летательный аппарат, состоящий из двух или более механически соединённых ракет, называемых ступенями, разделяющихся в полёте. Многоступенчатая ракета позволяет достигнуть скорости большей, чем каждая из её ступеней в отдельности.

Принцип действия многоступенчатой ракетыРакета является весьма «затратным» транспортным средством. Ракеты-носители космических аппаратов «транспортируют», главным образом, топливо, необходимое для работы их двигателей, и собственную конструкцию, состоящую в основном из топливных контейнеров и двигательной установки. На долю полезной нагрузки приходится лишь малая часть (1,5-2,0%) стартовой массы ракеты.

Составная ракета позволяет более рационально использовать ресурсы за счёт того, что в полёте ступень, выработавшая своё топливо, отделяется, и остальное топливо ракеты не тратится на ускорение конструкции отработавшей ступени, ставшей ненужной для продолжения полёта. Пример расчёта, подтверждающего эти соображения, приводится в статье Формула Циолковского.

Конструктивно многоступенчатые ракеты выполняются c поперечным или продольным разделением ступеней.

При поперечном разделении ступени размещаются одна над другой и работают последовательно друг за другом, включаясь только после отделения предыдущей ступени. Такая схема даёт возможность создавать системы, в принципе, с любым количеством ступеней. Недостаток её заключается в том, что ресурсы последующих ступеней не могут быть использованы при работе предыдущей, являясь для неё пассивным грузом.

Трёхступенчатая ракета-носитель с продольно-поперечным разделением Союз-2.При продольном разделении первая ступень состоит из нескольких одинаковых ракет (на практике, от 2-х до 8-и), работающих одновременно и располагающихся вокруг корпуса второй ступени симметрично, чтобы равнодействующая сил тяги двигателей первой ступени была направлена по оси симметрии второй. Такая схема позволяет работать двигателю второй ступени одновременно с двигателями первой, увеличивая, таким образом, суммарную тягу, что особенно нужно во время работы первой ступени, когда масса ракеты максимальна. Но ракета с продольным разделением ступеней может быть только двухступенчатой.

Существует и комбинированная схема разделения — продольно-поперечная, позволяющая совместить преимущества обеих схем, при которой первая ступень разделяется со второй продольно, а разделение всех последующих ступеней происходит поперечно. Пример такого подхода — отечественный носитель Союз.

Уникальную схему двухступенчатой ракеты с продольным разделением имеет космический корабль Спейс Шаттл, первая ступень которого состоит из двух боковых твёрдотопливных ускорителей, а на второй ступени часть топлива содержится в баках орбитера (собственно многоразового корабля), а большая часть — в отделяемом внешнем топливном баке. Сначала двигательная установка орбитера расходует топливо из внешнего бака, а когда оно будет исчерпано, внешний бак сбрасывается и двигатели продолжают работу на том топливе, которое содержится в баках орбитера. Такая схема позволяет максимально использовать двигательную установку орбитера, которая работает на всём протяжении вывода корабля на орбиту.

 

При поперечном разделении ступени соединяются между собой специальными секциями — переходниками — несущими конструкциями цилиндрической или конической формы (в зависимости от соотношения диаметров ступеней), каждый из которых должен выдерживать суммарный вес всех последующих ступеней, помноженный на максимальное значение перегрузки, испытываемой ракетой на всех участках полёта, на которых данный переходник входит в состав ракеты.

При продольном разделении на корпусе второй ступени создаются силовые бандажи (передний и задний), к которым крепятся блоки первой ступени.

Элементы, соединяющие части составной ракеты, сообщают ей жёсткость цельного корпуса, а при разделении ступеней должны практически мгновенно освобождать верхнюю ступень. Обычно соединение ступеней выполняется с помощью пироболтов. Пироболт — это крепёжный болт, в стержне которого рядом с головкой создается полость, заполняемая бризантным взрывчатым веществом с электродетонатором. При подаче импульса тока на электродетонатор происходит взрыв, разрушающий стержень болта, в результате чего его головка отрывается. Количество взрывчатки в пироболте тщательно дозируется, чтобы, с одной стороны, гарантировать отрыв головки, а, с другой — не повредить ракету. При разделении ступеней на электродетонаторы всех пироболтов, соединяющих разделяемые части, одновременно подаётся импульс тока, и соединение освобождается.

Далее ступени должны быть разведены на безопасное расстояние друг от друга. (Запуск двигателя высшей ступени вблизи низшей может вызвать прогар ее топливной емкости и взрыв остатков топлива, который повредит верхнюю ступень, или дестабилизирует её полет.) При разделении ступеней в атмосфере для их разведения может быть использована аэродинамическая сила встречного потока воздуха, а при разделении в пустоте иногда используются вспомогательные небольшие твёрдотопливные ракетные двигатели.

На жидкостных ракетах эти же двигатели служат и для того, чтобы «осадить» топливо в баках верхней ступени: при выключении двигателя низшей ступени ракета летит по инерции, в состоянии свободного падения, при этом жидкое топливо в баках находится во взвешенном состоянии, что может привести к сбою при запуске двигателя. Вспомогательные двигатели сообщают ступени небольшое ускорение, под действием которого топливо «оседает» на днища баков.

На приведённом выше снимке ракеты Сатурн-5, на корпусе третьей ступени (крайняя слева, в кадре представлена частично) виден чёрный корпус одного из вспомогательных твёрдотопливных двигателей разведения 3-й и 2-й ступеней.

Увеличение числа ступеней даёт положительный эффект только до определённого предела. Чем больше ступеней — тем больше суммарная масса переходников, а также двигателей, работающих лишь на одном участке полёта, и, в какой-то момент, дальнейшее увеличение числа ступеней становится контрпродуктивным. В современной практике ракетостроения более четырёх ступеней, как правило, не делается.

При выборе числа ступеней важное значение имеют также вопросы надёжности. Пироболты и вспомогательные РДТТ — элементы одноразового действия, проверить функционирование которых до старта ракеты невозможно. Между тем, отказ только одного пироболта может привести к аварийному завершению полёта ракеты. Увеличение числа одноразовых элементов, не подлежащих проверке функционирования, снижает надёжность всей ракеты в целом. Это также заставляет конструкторов воздерживаться от слишком большого количества ступеней.

Вопрос 9:

Закон сохранения механической энергии

1)Механическая работа – это процесс и мера изменения энергии.

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком: A = –(Eр2 – Eр1).

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел. Следовательно А=Е_к2-Е_к1 или Ek1 + Ep1 = Ek2 + Ep2.

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости.

2) КИНЕТИЧЕСКАЯ ЭНЕРГИЯ

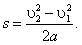Рассмотрим случай, когда на тело массой m действует постоянная сила F̅ (она может быть равнодействующей нескольких сил) и векторы силы F̅ и перемещения S̅ направлены вдоль одной прямой в одну сторону. В этом случае работу силы можно определить как A = F∙s. Модуль силы по второму закону Ньютона равен F = m∙a, а модуль перемещения s при равноускоренном прямолинейном движении связан с модулями начальной υ1 и конечной υ2 скорости и ускорения а выражением

 

Отсюда для работы получаем (1)

 

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела.

 

Кинетическая энергия обозначается буквой Ek.

 

(2)

 

Тогда равенство (1) можно записать в таком виде:

 

A = Ek2 – Ek1. (3)

 

Теорема о кинетической энергии:

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.

 

Если начальная скорость движения тела массой т равна нулю и тело увеличивает свою скорость до значения υ, то работа силы равна конечному значению кинетической энергии тела:

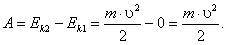
(4)

 

Физический смысл кинетической энергии:

кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ

Потенциальная энергия – это энергия взаимодействия тел.

Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Потенциальными называются силы, работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формы траектории.

При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторые другие.

Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.

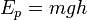
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения и определяется только начальным и конечным положениями тела. Такие силы называются консервативными.

Работа консервативных сил на замкнутой траектории равна нулю.

Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.

Работа консервативной силы A1a2 = A1b2. Работа на замкнутой траектории A = A1a2 + A2b1 = A1a2 – A1b2 = 0

Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести F̅=mg̅. Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения Δs̅ на ось OY, направленную вертикально вверх: ΔA = Fт Δs cos α = –mgΔs y,

где Fт = Fтy = –mg – проекция силы тяжести, Δsy – проекция вектора перемещения. При подъеме тела вверх сила тяжести совершает отрицательную работу, так как Δsy > 0. Если тело переместилось из точки, расположенной на высоте h1, в точку, расположенную на высоте h2 от начала координатной оси OY, то сила тяжести совершила работу A = –mg (h2 – h1) = –(mgh2 – mgh1).

 

Эта работа равна изменению некоторой физической величины mgh, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести Eр = mgh.

 

Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.

Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.A = –(Eр2 – Eр1).

Потенциальная энергия Eр зависит от выбора нулевого уровня, т. е. от выбора начала координат оси OY. Физический смысл имеет не сама потенциальная энергия, а ее изменение ΔEр = Eр2 – Eр1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.

Для сил всемирного тяготения потенциальную энергию удобно отсчитывать от бесконечно удаленной точки, т. е. полагать потенциальную энергию тела в бесконечно удаленной точке равной нулю. Формула, выражающая потенциальную энергию тела массой m на расстоянии r от центра Земли, имеет вид

где M – масса Земли, G – гравитационная постоянная.

 

Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.

Вопрос 10: