Свободные гармонические колебания. Период. Частота. Пружинный маятник. Дифференциальное уравнение гармонических колебаний, его решение.

В лекции тема «Колебательно движение».

По причине возникновения колебаний, их делят на:

1.свободные – колеб., происходящие под действием внутренних сил, возникающих в системе при выведении из равновесия.

2.вынужденные – колеб., происходящие под действием внешней, периодически меняющейся силы.

По закону (характеру изменяющейся координаты тела):

1.гармонические – происходят по закону синуса или косинуса.

2.негармонические.

Свободные гармонические колебания.

Период Т – время одного полного колебания

Частота (Ню или f) – число колебаний в единицу времени.

Ню=1/Т, [Гц]

Системы, в которых происходят свободные гармонические колебания:

1. Пружинный маятник.

Цель: x(t)-?

0 – недеформированное состояние пружины

Дельта l=x

ma = mg + Fупр + N (a, g, F, N - векторы)

X: ma_x = -Fупр

По опред. a_x = x^’’

По закону Гука: Fупр = k*дельта l = kx

x^’’ = -kx

x^’’ = -k/m*x

Обозначим ω² = k/m, тогда x^’’ = - ω² x

2. Математический маятник – математическая точка на невесомо растяжимом подвесе.

Цель: α(t) -?

Требования:

1) Масса груза значительно больше массы подвеса

2) Длина подвеса (l) значительно больше размера груза

I ε = ∑M (ε и M - векторы)

I = ml², По определению ε = α^’’

ml²* α^’’ = mgl*sin α

Пусть α – угол отклонения от положения равновесия маятника

sin α ≈ tg α ≈ α рад.

α^’’= -q/l* α

α^’’ = ω² α, т.к. - q/l = ω²

3. Физический маятник – любое тело с закрепленной осью вращения, с проходящей через центр масс.

Цель: α(t) -?

I ε = ∑M

I α^’’ = -mgl* α

α^’’ = -mgl/I* α

I^’’= ω² α, т.к. -mgl/I = ω

Вывод: для всех 3х маятников получили одинаковые дифференцированные уравнения, следовательно, решения одинаковые, следовательно, характер изменения координаты каждого из 3х маятников одинаковый.

Решение уравнения x^’’ = - ω² x ищут в виде: x(t) = Acos(ω₀t + фи₀)

Вывод: все 3 маятника совершаю гармонические колебания, ур-е вида: x^’’ = - Aω² x называют дифференциальным уравнением гармонических колебаний.

 

Вопрос 16:

16 Физический маятник - твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси О подвеса, не проходящей через центр масс С тела (рис.1).

Если маятник отклонен от положения равновесия на некоторый угол α, то в соответствии с уравнением динамики вращательного движения твердого тела момент М возвращающей силы F можно 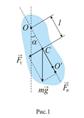записать в виде:

(4)

где J - момент инерции маятника относительно оси, проходящей через точку О; l - расстояние между точкой подвеса и центром масс маятника; F_τ -возвращающая сила (знак минус обусловлен тем, что направление F_τ и α всегда противоположны); sinα ≈ α соответствует малым колебаниям маятника, т.е. малым отклонениям маятника из положения равновесия.

 

Уравнение (4) можно записать в виде:

или

Принимая

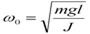
(5)

получим уравнение

решение которого имеет вид:

(6)

Из выражения (6) следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω _о и периодом:

(7)

 

где L - приведенная длина физического маятника, численно равная:

Приведенная длина физического маятника - длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физич. маятника.

Вопрос 17:

17Математический маятник - идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой, невесомой нити, и колеблющейся под действием силы тяжести (рис.2).

Период колебаний математического маятника:

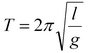
(8)

 

Циклическая частота математического маятника:

(9)

 

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ