Механическая работа как процесс и мера изменения энергии.

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.

Работой A, совершаемой постоянной силой называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы и перемещения A = Fs cos α.

Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).

Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.

Работа силы:

Если проекция F̅_S силы F̅ на направление перемещения s̅ не остается постоянной, работу следует вычислять для малых перемещений Δsi и суммировать результаты:

 

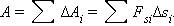
Это сумма в пределе (Δsi → 0) переходит в интеграл.

Графически работа определяется по площади криволинейной фигуры под графиком Fs(x)

Графическое определение работы. ΔAi = FsiΔsi

Примером силы, модуль которой зависит от координаты, может служить сила упругости пружины, подчиняющаяся закону Гука Fx = Fупр = –kx.. Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу модуль которой пропорционален удлинению пружины.

Растянутая пружина. Направление внешней силы совпадает с направлением перемещения k – жесткость пружины.

 

:

 

 

Этой формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы равна по модулю работе внешней силы и противоположна ей по знаку.

Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил.

Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

 

В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.

 

Вопрос 11:

11 Работа силы тяжести и силы упругости. Консервативные силы, потенциальные поля. Работа силы трения. Диссипативные силы.

Диссипати́вные си́лы — силы, при действии которых на механическую систему её полная механическая энергия убывает (то есть диссипирует), переходя в другие, немеханические формы энергии, например, в теплоту.
В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.
Потенциальные поля
Если работа сил поля, действующих на перемещающуюся в нём пробную частицу, не зависит от траектории частицы, и определяется только её начальным и конечным положениями, то такое поле называется потенциальным. Для него можно ввести понятие потенциальной энергии частицы — некоторой функции координат частиц такой, что разность её значений в точках 1 и 2 равна работе, совершаемой полем при перемещении частицы из точки 1 в точку 2.
Сила в потенциальном поле выражается через потенциальную энергию как ее градиент:
Ньютоново поле тяготения. Для поля материальной точки справедливо:
где — напряженность поля (ускорение свободного падения), - потенциальная энергия, M — масса материальной точки, — радиус-вектор, проведённый от материальной точки в точку наблюдения, r — длина этого радиуса-вектора, m — масса пробной частицы, G — некая константа (называемая гравитационной постоянной), численное значение которой зависит от выбранной системы единиц измерения.
О силе трения скольжения
Нередко говорят, что сила трения скольжения всегда совершает отрицательную работу и это приводит к увеличению внутренней (тепловой) энергии системы.
Такое утверждение нуждается в важном уточнении — оно справедливо только в том случае, если речь идет не о работе одной отдельно взятой силы трения скольжения, а о суммарной работе всех таких сил, действующих в системе. Дело в том, что работа любой силы зависит от выбора системы отсчета и может быть отрицательной в одной системе, но положительной в другой. Суммарная же работа всех сил трения, действующих в системе, не зависит от выбора системы отсчета и всегда отрицательна. Вот конкретный пример.
Положим кирпич на движущуюся тележку так, чтобы он начал по ней скользить (рис. 1). В системе отсчета, связанной с землей, сила трения F1, действующая на кирпич до, прекращения скольжения, совершает положительную работу A1. Одновременно сила трения F2, действующая на тележку (и равная по модулю первой силе), совершает отрицательную работу A2, по модулю большую, чем работа A1, так как путь тележки s больше пути кирпича s - l (l — путь кирпича относительно тележки). Таким образом, получаем
,и полная работа сил трения.Поэтому кинетическая энергия системы убывает (переходит в тепло):
Этот вывод имеет общее значение. Действительно, работа двух сил (не только сил трения), осуществляющих взаимодействие между телами, не зависит от выбора системы отсчета (докажите это самостоятельно). Всегда можно перейти к системе отсчета, относительно которой одно из тел покоится. В ней работа силы трения, действующей на движущееся тело, всегда отрицательна, так как сила трения направлена против относительной скорости. Но она отрицательна и в любой другой системе отсчета. Следовательно, всегда, при любом количестве тел в системе, Atr < 0. Эта работа и уменьшает механическую энергию системы.
О силе трения покоя
При действии между соприкасающимися телами силы трения покоя ни механическая, ни внутренняя (тепловая) энергия этих тел не изменяется. Значит ли это, что работа силы трения покоя равна нулю? Как и в первом случае, такое утверждение правильно только по отношению к полной работе сил трения покоя над всеми взаимодействующими телами.

Вопрос 12:

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек. Осевые моменты инерции некоторых тел.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,где:

§ m_i — масса i -й точки,

§ r_i — расстояние от i -й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

,где:

§ — масса малого элемента объёма тела ,

§ — плотность,

§ — расстояние от элемента до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

Теорема Гюйгенса-Штейнера

Основная статья: Теорема Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласнотеореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

Если — момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии от неё, равен

,

где — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

Вопрос 13: