Регрессионный анализ – вид статистического анализа, занимающийся изучением причинно-следственных связей двух или более количественных переменных, включающий в себя:
- определение формы связи;
- построение уравнения регрессии;
- оценку полученного уравнения.
Уравнение регрессии приближенно выражает зависимость среднего значения, объясняемого (зависимого) признака от одного или нескольких признаков-факторов. Наиболее часто используются регрессионные модели, в которых одна зависимая переменная функция и несколько независимых переменных факторов.
Основные требования регрессионного анализа к исходным данным:
- все переменные количественные;
- совокупность данных достаточно большая, чтобы показатели связи были статистически надежными (число единиц совокупности превосходит число коррелируемых переменных не менее чем в 6-8 раз);
- наблюдения статистически независимые, то есть, значения признаков у одной единицы наблюдения не должны зависеть от значения признака у других единиц совокупности;
- в регрессионном анализе предполагается, что каждому значению фактора х соответствует нормальное или близкое к нему распределение объясняемого или зависимого признака у;
- в модели множественной регрессии (несколько признаков-факторов) отсутствует явление мультиколлиниарности (признаки-факторы не коррелируют друг с другом).
Уравнение регрессии, описывающее зависимость объясняемого признака (у) от одного признака-фактора (х), называется уравнением парной регрессии. Могут быть разного вида в зависимости от того, линейна или нелинейна связь между изучаемыми признаками
Уравнение парной линейной связи: y = a + bx
Уравнение парной нелинейной связи: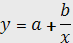 
y = a + bx + cx2
y = alogx
При построении модели нужно убедиться, линейна или нелинейная связь. Первый шаг РА – построение диаграммы рассеяния.
В УПЛС a (свободный член уравнения регрессии и отражает действие на зависимый признак у, не учтенных в уравнении регрессии факторов; как правило, не интерпретируется; знак зависит от соотношения вариации (дисперсия, СКО) у и х: если у варьирует сильнее, чем х, то минус, и наоборот) и b (коэффициент регрессии; сила связи изучаемых признаков и то, насколько в среднем изменится у при изменении на 1 признака-фактора – зависимый признак изменяется на коэффициент регрессии b) являются параметрами уравнения регрессии. Графическое изображение уравнения регрессии – теоретическая линия регрессии. При линейной зависимости коэффициента регрессии представляет собой тангенс угла наклона теоретической линии регрессии к оси х. Знак при коэффициенте b показывает направление связи. Пересечение теоретической линии регрессии с осью у соответствует значению свободного члена уравнения регрессии a.
Чтобы построить УР, необходимо рассчитать параметры a и b (должен быть средними для всей совокупности данных, чтобы выявить закон связь свободный от нарушений). При нахождении параметров регрессии исходим из того, что сумма квадратов отклонений от среднего арифметического меньше суммы квадратов отклонений от любой другой величины. Такой подход к расчету параметров регрессии называется методом наименьших квадратов.
Формулы вычисления:
-------------> 
После того как будут вычислены параметры уравнения регрессии, возникает задача оценки качества полученного уравнения (полученной регрессионной модели). Нужно подставить значения хi в формулу уравнения и получим вычисленные значения уi (
).
От реальных значений уi вычесть значения уi. 
. Полученная разность позволяет найти величину, называемой остаточной дисперсией (дисперсией остатков):
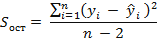
Выступает в качестве критерия оценки найденного уравнения. Чем меньше вычисленное значение отличается от реального значения уi, тем меньше величина остаточной дисперсии, тем качественнее полученная регрессионная модель. Существует ещё один способ оценки регрессии по величине коэффициента детерминации – возведенный в квадрат линейный коэффициент корреляции Пирсона.
Показывает процент дисперсии зависимого признака у, объясняемый действием независимого признака фактора х.
Если коэффициент превышает 30%, то полученная модель качественная.
