Анализируя связь 2-х количественных признаков, мы отвечаем на вопросы:
1) существует ли связь между изучаемыми признаками;
2) насколько эта связь сильна;
3) каково направление связи;
4) линейная или не линейная связь.
Корреляционный анализ предполагает изучение связи в два этапа:
1) построение диаграммы рассеяния и ее анализ;
2) вычисление коэффициента и его анализ.
Диаграмма рассеяния – двумерный график, по одной оси которого откладываются значения одной переменной, а по другой оси – другой переменной. Объекты изображаются в виде точек с координатами, равными значениям переменных для объекта. Получаем облако точек или облако рассеяния. С помощью диаграммы рассеяния мы можем предварительно оценить наличие связи, направление связи, силу связи, линейность связи. Виды диаграмм рассеяния:

1) является довольно плотным, вытянутым, наклон влево. Связь есть (всегда, если облако имеет наклон к оси х). При увеличении значения х значение у увеличивается, значит, такая связь называется прямой положительной. Связь сильная, так как облако точек является плотным. Связь является линейной, так как через облако точек можно провести воображаемую прямую;
2) связь есть, так как наклон. Если при увеличении х значение у уменьшается, значит, связь отрицательная обратная. Связь сильная. Связь линейная;
3) связь есть, обратная, слабая, линейная;
4) связь есть, прямая, слабая, линейная;
5) связь отсутствует;
6) связь есть, сильная, нелинейная.
Линейный коэффициент корреляции Пирсона. В основе построения коэффициента Пирсона лежит ковариация – совместное отклонение изучаемых признаков от средних арифметических. Стоится на основе дисперсии.


Ковариация, в отличие от дисперсии, имеет знак. Знак ковариации указывает на направление связи. Не может быть мерой связь двух количественных признаков, так как ее значение не попадают в интервал от -1 до 1. Поэтому ковариацию нормируют делением на среднеквадратическое отклонение по х и по у. Отношение ковариации к СКО по х и по у и есть линейный коэффициент корреляции Пирсона.
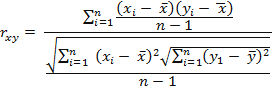
Свойства:
- изменяется в интервале от -1 до 1;
- равен 0, если ковариация равна 0; отсутствие линейной связи;
- если значение коэффициент равно -1 или 1 – присутствует полная обратная или прямая статистическая связь;
- если значения коэффициент изменяются от 0 (не включая) до 0,3 – сила связи слабая; от 0,3 до 0,6 – средняя; от 0,6 до 1 (не включая) – сильная.
Проверка гипотезы о статистической значимости коэффициента Пирсона. Статистически значим, если его значение для ГС отлично от 0.
H0:rгсxy = 0
H1:rгсxy ≠ 0

df = n – 2
|tH| > 







