Н.Р. – симметричный колокол, центр которого расположен в точке мю µ (математическое ожидание – среднее арифметическое для генеральной совокупности), а ширина зависит от сигмы ϭ (среднеквадратичное отклонение от генеральной совокупности) (являются параметрами НР). Обозначается N(µ; ϭ). В зависимости от значений µ и ϭ изменяется и колокол НР. (1)
Существует бесконечное множество НР, определяемых значениями µ и ϭ.
Свойства кривой НР:
1) симметрична относительно точки µ, причем для НР характерно совпадения µ, моды и медианы;
2) асимптотически приближается к оси Х-ов, продолжаясь в обе стороны до бесконечности. Следовательно, чем больше значение отклоняется от µ, тем реже они встречаются;
3) имеет 2 точки перегиба, находящиеся на расстоянии ±ϭ от µ;
4) при µ, равном константе, увеличение ϭ кривая становится более пологой. При ϭ, равной константе, с изменением µ кривая не меняет свою форму, а двигается вправо/влево по оси Х;
5) правило трех сигм: в промежутке µ ±ϭ находится 68,3% всех наблюдаемых значений;
µ ±2ϭ 95,4%;
µ ±3 ϭ 99,7%.
Для того чтобы стандартизировать (унифицировать) множество НР, вводятся НР с параметрами µ = 0 и ϭ = 1. Такое Распределение получило название Стандартное Нормальное Распределение. Обозначается Z (0;1). Параметры СНР являются 0 и 1.
Переход от произвольного НР к СНР и обратно происходит по формуле Z-оценки: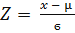 
.
При переходе в стандартный масштаб изменяется масштаб измерения, но остается неизменной. Свойства Z-оценки:
1) СА всегда = 0;
2) дисперсия и СКО всегда = 1;
3) её знак показывает, в какую сторону от СА отклоняется конкретная Z-оценка;
4) если её значение превышает 3 или -3, фиксируется значительное отклонение конкретной Z-оценки от СА. Такое отклонение называют выбросом.
Для СНР рассчитывают статистическую таблицу, с помощью которой можно решать задачи 2-х типов:
1. 1) для заданного числа а определить значение функций распределения F (a) и далее использовать её для определения любой необходимой вероятности (1 – прошлый рисунок);
Вероятность P того, что случайная величина Х попадет слева от точки а = F(a). P(x<a) = F(a);
2) (2) P(x>a) = 1- F(a);
3) (3) P(a<x<b) = F(b)-F(a).
2. 1) для заданной вероятности найти соответствующую точку. Рассматриваем только 1. 1) слева от искомой точки.
P(Z<1,58) = 0,94235
P(Z<3,12) = 0,9990357
Квадрат обозначает количество цифры 9.
P(Z>0,71) = 1 - 0,7611 = 0,2389
P = 0,98030 a = 2,06
Для СНР выполняется свойство симметричности: P(x<-a) = P(x>a):
Вероятность попадания в область слева от точки -а = вероятности попадания в область справа от точки а.
N(5;3);
P(x>2).
Другие распределения
1. Распределение Т-Стьютенда - симметричный колокол с центром в точке 0, вид которого зависит от параметра под названием число степеней свободы: 
.
Чем больше df, тем более плоский график; чем меньше df, тем более острый график.
Если ЧСС имеет малое значение, то колокол вытягивается, и наоборот.
При объёмах выборки n>50 приближается и впоследствии совпадает с нормальным распределением.
Таблица:
Внутри – точки;
Слева – ЧСС;
Верх – вероятности.
2. Распределение x2 (хи-квадрат) Пирсона - ассиметричный колокол с длинным правым хвостом и началом в точке 0. Форма колокола задается параметром “ЧСС”.
3. F-Распределение Фишера – ассиметричный колокол с длинным правым хвостом и началом в точке 0. Форма задается ЧСС для 2-х независимых выборочных совокупностей
