Если все варианты увеличить на 3, то коэффициент корреляции…
+ не изменится
- уменьшиться на 3
- увеличится в 3 раза
- увеличится в 9 раз
- уменьшиться на 9
Если все варианты увеличить на 5, то коэффициент корреляции…
+ не изменится
- уменьшиться на 5
- увеличится в 5 раза
- увеличится в 25 раз
- уменьшиться на 25
Если все варианты увеличить на 4, то коэффициент корреляции…
+ не изменится
- уменьшиться на 4
- увеличится в 4 раза
- увеличится в 16 раз
- уменьшиться на 16
Внутригрупповая дисперсия вычисляется по формуле…
- 
+ 
- 
- 
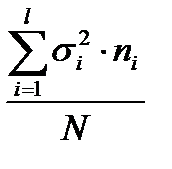
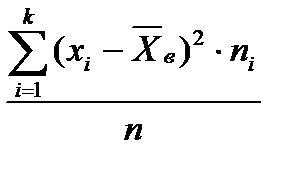
Межгрупповая дисперсия вычисляется по формуле…
-
-
+
-
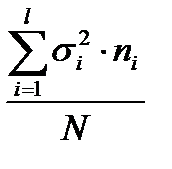
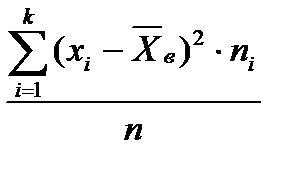
Общая дисперсия вычисляется по формуле…
+
-
-
-
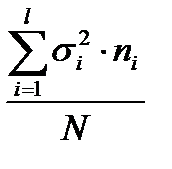
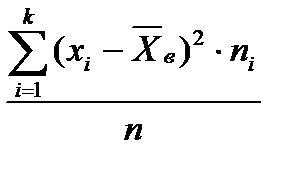
Выборочное уравнение парной регрессии имеет вид у= -3,2+1,6 х. Тогда выборочный коэффициент регрессии равен …
- – 3,2
- –1,6
+ 1,6
- 3,2
Выборочное уравнение парной регрессии имеет вид у= -4,3+0,4х. Тогда выборочный коэффициент регрессии равен …
+ 0,4
- –4,3
- –0,4
- 4,3
Выборочное уравнение парной регрессии имеет вид у=2,8+1,3х. Тогда выборочный коэффициент регрессии равен …
- –1,3
+ 1,3
- –2,8
- 2,8
Выборочное уравнение парной регрессии имеет вид у= -2,6+1,3х. Тогда выборочный коэффициент корреляции может быть равен …
- –2,6
- 2,6
- –0,8
+ 0,8
Выборочное уравнение парной регрессии имеет вид у= 2,5+1,25х. Тогда выборочный коэффициент корреляции может быть равен …
+ 0,75
- –0,5
- –2,8
- 1,25
Выборочное уравнение парной регрессии имеет вид у= 6,4-1,6х. Тогда выборочный коэффициент корреляции может быть равен …
- –4,0
+ –0,95
- 4,0
- 0,92
Выборочное уравнение парной регрессии имеет вид у=2,8+0,8х, средние квадратические отклонения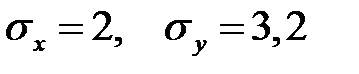 
. Тогда коэффициент корреляции равен … Результат округлите до сотых.
- 5,12
+ 0,5
- –0,5
- 3,36
Выборочное уравнение парной регрессии имеет вид у=3,6+0,6х, средние квадратические отклонения 
. Тогда коэффициент корреляции равен … Результат округлите до сотых.
+ 0,29
- 2,05
- –2,05
- 5,42
Выборочное уравнение парной регрессии имеет вид у= -1,48+3,9х, средние квадратические отклонения 
. Тогда коэффициент корреляции равен … Результат округлиеь до сотых.
- 0,98
- 4,71
- –0,05
+ 0,9
При построении выборочного уравнения парной регрессии вычислен выборочный коэффициент корреляции 
и выборочные средние квадратические отклонения 
. Тогда выборочный коэффициент регрессии Y на Х равен …
- –1,72
- 0,43
+ 1,72
- 8,05
При построении выборочного уравнения парной регрессии вычислен выборочный коэффициент корреляции 
и выборочные средние квадратические отклонения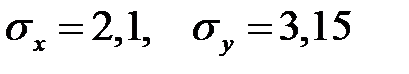 
. Тогда выборочный коэффициент регрессии Y на Х равен …
- –1,63
- 0,6
- 5,95
+ 1,35
При построении выборочного уравнения парной регрессии вычислен выборочный коэффициент корреляции 
и выборочные средние квадратические отклонения 
. Тогда выборочный коэффициент регрессии Y на Х равен …
+ 1,26
- 0,32
- 3,64
- –1,17
Элементы комбинаторики
Количество перестановок из букв слова «корсаж», в которых буква «к» на первом месте, а буква «ж» - в конце слова, равно …
- 120
- 6
+ 24
- 620
Количество перестановок из букв слова «лидер», в которых буква «е» на первом месте, а буква «д» - в конце слова, равно …
- 4
+ 6
- 5
- 3
Количество перестановок из букв слова «планета», в которых буква «е» на первом месте, а буква «п» - в конце слова, равно …
- 24
+ 120
- 5
- 15
Количество перестановок букв слова «бином» равно …
- 5
- 24
- 20
+ 12
Количество перестановок букв слова «угол» равно …
- 4
- 120
+ 24
- 20
Количество перестановок букв слова «граф» равно …
+ 24
- 5
- 120
- 20
В коробке 6 цветных карандашей. Число способов выбрать два из них равно …
15
Число способов выбрать из группы в 20 студентов двух дежурных равно …
Число способов выбрать из группы в 20 студентов старосту и заместителя равно …
Из ящика, где находится 13 деталей, пронумерованных от 1 до 13, требуется вынуть 5 деталей. Тогда количество всевозможных комбинаций номеров вынутых деталей равно …
- 
- 13!
+ 
- 5!
В цветочном киоске 7 видов цветов. Количество способов выбора 3 цветов различно вида равно …
+ 
- 
- 7!
- 3!
На собрании членов кооператива присутствуют 20 человек. Тогда количество комбинаций выбора председателя правления, его заместителя и бухгалтера равно …
- 
+ 
- 
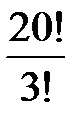
- 20!
Соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, которые отличаются друг от друга, либо самими элементами, либо порядком их расположения.
- перестановки
- сочетания
+ размещения
- события
- величины
Соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, которые отличаются друг от друга, по крайней мере, одним элементом.
- перестановки
+ сочетания
- размещения
- величины
- события
Соединения, из которых каждое содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.
+ перестановки
- сочетания
- размещения
- величины
- события
Количество перестановок слова «свитер», в которых буква «с» на первом месте равно
- 24
- 625
+ 120
- 720
Сколькими способами можно с помощью букв M, N, R, F, S обозначить вершины пятиугольника.
- 1
- 5
- 24
+ 120
Сколькими способами можно сформировать команду из 4 студентов для участия в командной олимпиаде из 10 претендентов.
+ 210
- 24
- 720
- 14
Сколько трехзначных чисел можно составить из множества цифр {1,2,5,6,7,8}, если все цифры в нем различные.
- 720
+ 120
- 6
- 18
Количество перестановок в слове «книга» равно…
+ 120
- 20
- 24
- 5
На занятии по математике преподаватель разбивает группу студентов по 4 человек. Сколько групп может быть образовано в группе из 24 студентов?
- 255024
+ 10626
- 212520
- 12144
Сколько существует семизначных чисел, состоящих из цифр 4, 5 и 6, в котором цифра 4 повторяется 3 раза, а цифры 5 и 6 – по 2 раза?
- 120
+ 210
- 5040
- 96
Сколькими способами можно сформировать команду из 4 человек для участия в спортивных соревнованиях из 8 претендентов.
+ 70
- 35
- 10
- 1260
Если «словом» считать любую комбинацию букв, то число «слов», полученных перестановкой букв в слове «РАМА», равно…
- 24
- 11
- 1
+ 12
