Может ли при каком-либо значении аргумента плотность распределения быть отрицательной?
- да, при х> 0
+ нет
- да, при х <0
- да
Может ли при каком-либо значении аргумента интегральная функция распределения вероятностей быть отрицательной?
- да, при х> 0
+ нет
- да, при х <0
- да
Может ли при каком-либо значении аргумента интегральная функция распределения вероятностей быть больше 1.
- да, при х> 0
+ нет
- да, при х <0
- да
Может ли при каком-либо значении аргумента дифференциальная функция распределения вероятностей быть больше 1.
- да, при х> 0
- нет
- да, при х <0
+ да
Может ли при каком-либо значении аргумента интегральная функция распределения вероятностей быть равной 0.
- да, при х> 0
- нет
- да, при х <0
+ да
Случайная величина задана дифференциальной функцией. Тогда  равна …
равна …
+ 
- 
- 
- 
Случайная величина задана интегральной функций распределения вероятностей. Тогда  равна …
равна …
- 
+ 
- 
- 
Известна дифференциальная функция. Тогда интегральную функцию можно найти по формуле …
- 
- 
- 
+ 
Известна интегральная функция. Тогда дифференциальную функцию можно найти по формуле …
- 
- 
+ 
- 
Случайная величина задана интегральной функций распределения вероятностей. Тогда математическое ожидание случайной величины можно найти по формуле …
- 
- 
+ 
- 
Непрерывная случайная величина задана функций распределения вероятностей  Тогда P(Х<0) равна …
Тогда P(Х<0) равна …
- 0
+ 0,75
- 0,5
- 1
Непрерывная случайная величина задана функций распределения вероятностей  Тогда P(Х>1) равна …
Тогда P(Х>1) равна …
- 0
- 0,5
+ 1
- 1,5
Непрерывная случайная величина задана функций распределения вероятностей  Тогда P(Х<-0,5) равна …
Тогда P(Х<-0,5) равна …
- 1
- 0,0025
- 0,5
+ 0
Непрерывная случайная величина задана Х интегральной функцией распределения вероятностей

Тогда значение С равно …
+ 0
- 0,5
- 2,25
- 1
Непрерывная случайная величина задана Х интегральной функцией распределения вероятностей
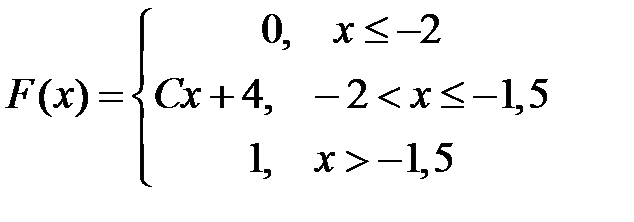
Тогда значение С равно …
- 4
+ 2
- – 1
- – 1,75
Непрерывная случайная величина задана Х дифференциальной функцией распределения вероятностей

Тогда значение С равно …
- 4/5
+ 3/8
- 1
- 5/8
Случайная величина Х починена нормальному закону с  . Тогда
. Тогда  имеет вид…
имеет вид…
- 
- 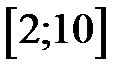
- 
+ 
Случайная величина Х починена нормальному закону с 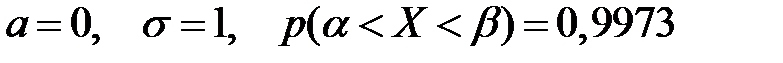 . Тогда
. Тогда  имеет вид…
имеет вид…
- 
- 
+ 
- 
Случайная величина Х починена нормальному закону с 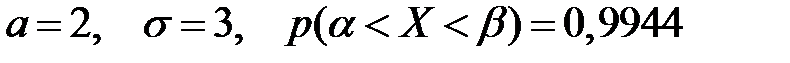 . Тогда
. Тогда  имеет вид…
имеет вид…
- 
- 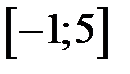
+ 
- 
Случайная величина Х починена нормальному закону с  . Тогда длина интервала, в который попадает Х равна …
. Тогда длина интервала, в который попадает Х равна …
- 15 мм
- 45 мм
+ 10 мм
- 30 мм
Случайная величина Х починена нормальному закону с  . Тогда длина интервала, в который попадает Х равна …
. Тогда длина интервала, в который попадает Х равна …
- 8 мм
+ 16 мм
- 24 мм
- 4 мм
Случайная величина Х починена нормальному закону с  . Тогда длина интервала, в который попадает Х равна …
. Тогда длина интервала, в который попадает Х равна …
- 9 мм
- 6 мм
+ 18 мм
- 3 мм
Случайная величина Х починена нормальному закону с  . Как изменится график плотности распределения, если
. Как изменится график плотности распределения, если  ?
?
+ сдвинется вправо на 3 единицы
- сдвинется влево на 3 единицы
- масштаб по оси Ох утроится
- масштаб по оси Оy утроится
Случайная величина Х починена нормальному закону с  . Как изменится график плотности распределения, если
. Как изменится график плотности распределения, если  ?
?
- сдвинется вправо на 3 единицы
+ сдвинется влево на 3 единицы
- масштаб по оси Ох утроится
- масштаб по оси Оy утроится
Случайная величина Х починена нормальному закону с  . Как изменится график плотности распределения, если
. Как изменится график плотности распределения, если  ?
?
- не изменится
- сдвинется вправо на 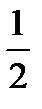 единицы
единицы
- масштаб по оси Оу уменьшится вдвое
+ масштаб по оси Оу увеличится вдвое
Случайная величина Х распределена по нормальному закону  . Тогда математическое ожидание и дисперсия случайной величины соответственно равны…
. Тогда математическое ожидание и дисперсия случайной величины соответственно равны…
- a =2; 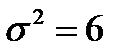
+ a =1; 
- a =0; 
- a =0, 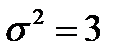
Случайная величина Х распределена по нормальному закону  . Тогда математическое ожидание и дисперсия
. Тогда математическое ожидание и дисперсия
случайной величины соответственно равны…
- a =0; 
- a =0; 
+ a =2; 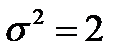
- a =1, 
Случайная величина Х распределена нормально по закону  . Тогда математическое ожидание и дисперсия случайной величины соответственно равны…
. Тогда математическое ожидание и дисперсия случайной величины соответственно равны…
- a =0; 
- a =0; 
+ a =4; 
- a =1, 
Если математическое ожидание и дисперсия случайной величины Х, распределенной по нормальному закону, соответственно равны: a= 1,  то функция плотности распределения вероятностей имеет вид…
то функция плотности распределения вероятностей имеет вид…
+ 
- 
- 
- 
Если математическое ожидание и дисперсия случайной величины Х, распределенной по нормальному закону, соответственно равны: a= 3,  то функция плотности распределения вероятностей имеет вид…
то функция плотности распределения вероятностей имеет вид…
- 
- 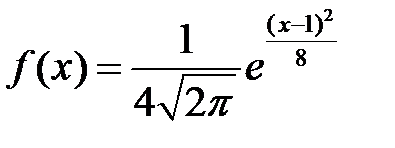
+ 
- 
Если математическое ожидание и дисперсия случайной величины Х, распределенной по нормальному закону, соответственно равны: a= 5,  то функция плотности распределения вероятностей имеет вид…
то функция плотности распределения вероятностей имеет вид…
- 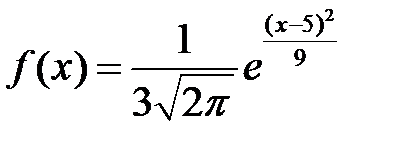
- 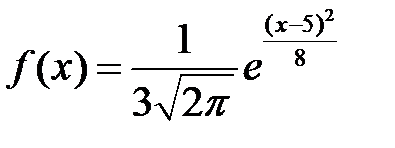
+ 
- 
Непрерывная случайная величина Х задана плотностью распределения вероятностей  . Тогда математическое ожидание этой нормально распределенной величины равно...
. Тогда математическое ожидание этой нормально распределенной величины равно...
- 9
- 162
- 81
+ 10
Непрерывная случайная величина Х задана плотностью распределения вероятностей  . Тогда математическое ожидание этой нормально распределенной величины равно...
. Тогда математическое ожидание этой нормально распределенной величины равно...
+ 5
- 4
- 16
- 32
Непрерывная случайная величина Х задана плотностью распределения вероятностей  . Тогда математическое ожидание этой нормально распределенной величины равно...
. Тогда математическое ожидание этой нормально распределенной величины равно...
- 7
- 98
+ 6
- 49
Случайная величина Х распределена равномерно на отрезке  . Тогда случайная величина Y =3 X –1 имеет...
. Тогда случайная величина Y =3 X –1 имеет...
- равномерное распределение на отрезке 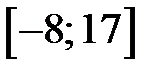
- нормальное распределение на отрезке 
- другой (кроме равномерного и нормального) вид распределения
+ равномерное распределение на отрезке 
Случайная величина Х распределена равномерно на отрезке  . Тогда случайная величина Y=3X–1 имеет...
. Тогда случайная величина Y=3X–1 имеет...
- равномерное распределение на отрезке 
- нормальное распределение на отрезке 
- другой (кроме равномерного и нормального) вид распределения
+ равномерное распределение на отрезке 
Случайная величина Х распределена равномерно на отрезке  . Тогда случайная величина Y =3 X –1 имеет...
. Тогда случайная величина Y =3 X –1 имеет...
+ равномерное распределение на отрезке 
- нормальное распределение на отрезке 
- другой (кроме равномерного и нормального) вид распределения
- равномерное распределение на отрезке 
График плотности распределения вероятностей непрерывной случайной величины Х, распределенной равномерно в интервале (-3; 2), имеет вид

Тогда значение a равно …
+ 0,2
- 0,25
- 0,4
- 1
График плотности распределения вероятностей непрерывной случайной величины Х, распределенной равномерно в интервале (-2; 5), имеет вид

Тогда значение a равно …
- 1/3
- 1/5
- 1
+ 1/7
График плотности распределения вероятностей непрерывной случайной величины Х, распределенной равномерно в интервале (-1; 3), имеет вид

Тогда значение a равно …
- 1
+ 0,25
- 0,2
- 0,33






