Основные понятия теории вероятностей
Вероятность невозможного события равна…
- 0,01
- –1
+ 0
- 1
Вероятность наступления некоторого события не может быть равна…
+ 1,2
- 0,2
- 0
- 0,8
Для вероятности р(А) любого случайного события выполнено условие
- р(А)<1
- р(А) >0
+ 0< р(А) <1
- р(А) >1
Вероятность достоверного события равна…
- 0
- –1
- 0,0002
+ 1
Из приведенных событий случайными являются …
Укажите не менее двух вариантов ответа
- «Выбор черного шара из урны с белыми шарами»
+ «Выпадение 6 очков при бросании игральной кости»
- «Выбор белого шара из урны с белыми шарами»
+ «Выбор черного шара из урны с белыми и черными шарами»
- «Выбор черного шара из урны с черными шарами»
- «Выбор белого шара из урны с черными шарами»
Из приведенных событий невозможными являются …
Укажите не менее двух вариантов ответа
+ «Замерзание воды при температуре +300»
- «Выпадение 6 очков при бросании игральной кости»
+ «Выбор черного шара из урны с белыми шарами»
- «Наступление лета после весны»
- «Выбор черного шара из урны с черными шарами»
- «Выбор черного шара из урны с белыми и черными шарами»
Из приведенных событий несовместными являются…
Укажите не менее двух вариантов ответа
- «Выбивание менее 5 очков при стрельбе по мишени» и «Выбивание четного числа очков при стрельбе по мишени»
+ «Выбивание менее 5 очков при стрельбе по мишени» и «Выбивание от 7 до 10 очков при стрельбе по мишени»
+ «Появление 6 при бросании игральной кости» и «Появление 4 при бросании игральной кости»
+ «Наступление ночи» и «Восход солнца»
- «Появление 2 при бросании игральной кости» и «Появление четного числа очков при бросании игральной кости»
- «Получение 5 на экзамене» и «Получение положительной оценки на экзамене»
Из приведенных величин дискретными случайными величинами являются…
Укажите не менее двух вариантов ответа
- «Значение функции f(x)=x на множестве действительных чисел»
- «Количество секунд в одном часе»
+ «Число очков выпадающих при бросании игральной кости»
+ «Количество мальчиков рожденных в тот или иной год»
- «Количество сантиметров в одном метре»
- «Количество этажей в шестнадцатиэтажном доме»
Из приведенных событий достоверными являются …
Укажите не менее двух вариантов ответа
- «Выпадение 6 очков при бросании игральной кости»
+ «Наступление лета после весны»
+ «Выбор черного шара из урны с черными шарами»
- «Замерзание воды при температуре +300»
- «Выбор черного шара из урны с белыми шарами»
- «Выбор белого шара из урны с белыми и черными шарами»
Из каждой из двух колод вынимают по одной карте. Событие А – «карта из первой колоды – туз» и В – «карта из второй колоды – дама» являются:
Укажите не менее двух вариантов ответа
- зависимыми
+ независимыми
+ совместными
- несовместными
- равновозможными
- противоположными
Бросают два кубика. Событии А – «на первом кубике выпало три очка» и В – «на втором кубике выпало шесть очков» являются:
Укажите не менее двух вариантов ответа
- зависимыми
+ независимыми
+ совместными
- несовместными
- достоверными
- случайными
Бросают 2 монеты. Событие А – «цифра на первой монете» и В – «герб на второй монете» являются:
Укажите не менее двух вариантов ответа
- зависимыми
+ независимыми
+ совместными
- несовместными
- случайными
- противоположными
События, которые обязательно произойдут, если будет осуществлена определенная совокупность условий, называются...
- случайные
- невозможные
+ достоверные
- совместные
- несовместные
События, которые заведомо не произойдут, если будет осуществлена определенная совокупность условий, называются....
- случайные
+ невозможные
- достоверные
- совместные
- несовместные
События, которые при осуществлении совокупности условий могут либо произойти, либо не произойти, называются...
+ случайные
- невозможные
- достоверные
- совместные
- несовместные
События, если появления одного из них исключает появление других событий в одном и том же испытании, называются …
- случайные
- невозможные
- достоверные
- совместные
+ несовместные
События, если появления одного из них не исключает появление других событий в одном и том же испытании, называются …
- случайные
- невозможные
- достоверные
+ совместные
- несовместные
События, если есть основания считать, что ни одно из них не является более возможным, чем другие, называются …
+ равновозможные
- противоположные
- единственно возможные
- полная группа событий
- совместные
Два единственно возможных и несовместных события называются …
- равновозможные
+ противоположные
- единственно возможные
- полная группа событий
- совместные
События, если при испытании появление одного и только одного из них является достоверным событием, называются...
- равновозможные
- противоположные
+ единственно возможные
- полная группа событий
- совместные
События, единственно возможные и несовместные называются …
- равновозможные
- противоположные
- единственно возможные
+ полная группа событий
- совместные
Несовместные события А, В и С не образуют полную группу, если их вероятности равны...
Укажите не менее двух вариантов ответа
- 
- 
+ 
+ 
- 
- 
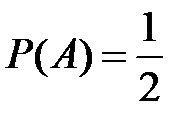
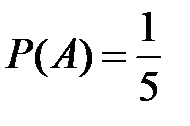
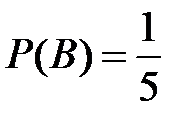
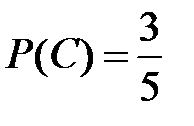
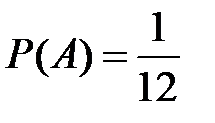
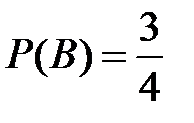
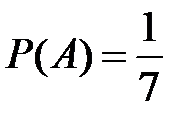
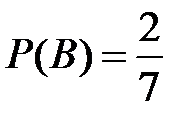
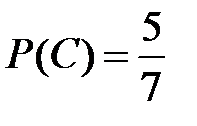
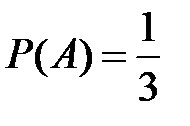
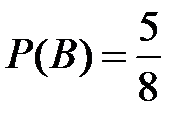
Несовместные события А, В и С не образуют полную группу, если их вероятности равны...
Укажите не менее двух вариантов ответа
+ 
+ 
- 
-
-
- 
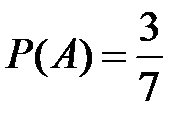
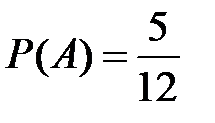
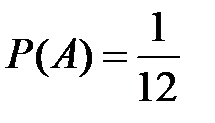
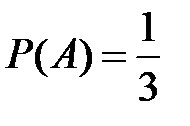
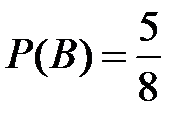
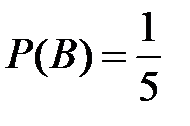
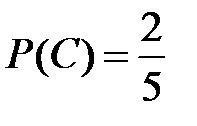
Несовместные события А, В и С не образуют полную группу, если их вероятности равны...
Укажите не менее двух вариантов ответа
-
-
- 
- 
+ 
+ 
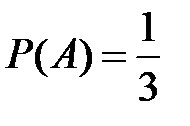
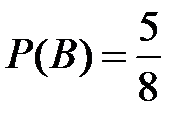
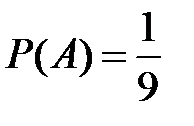
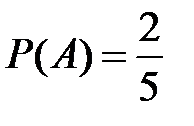
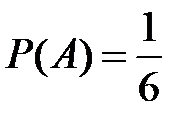
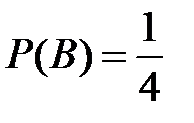
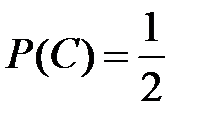
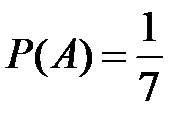
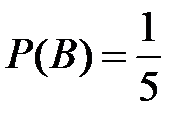
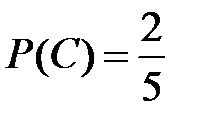
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее пяти очков, равна...
- 
- 
- 
+ 
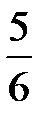
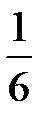
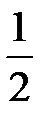
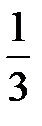
Вероятность того, что при бросании игрального кубика выпадет 1, или 2, или 6, составляет...
-
+
- 
-
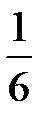
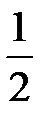
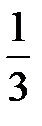
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет 5 очков, равна...
- 0,2
- 
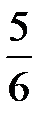
- 0,1
+ 
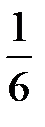
Теоремы сложения и умножения вероятностей
А,В,С – попарно независимые события. Их вероятности: р(А)=0,9, р(В)=0,3, р(С)=0,4. Укажите соответствие между событиями и их вероятностями:
1. 
2. 
3. 
4. 
2. 0,36
- 0,7
3. 0,12
4. 0,108
1. 0,27
А,В,С – попарно независимые события. Их вероятности: р(А)=0,4, р(В)=0,8, р(С)=0,3. Укажите соответствие между событиями и их вероятностями:
1.
2.
3.
4.
3. 0,24
- 0,5
2. 0,12
4. 0,096
1. 0,32
А,В,С – попарно независимые события. Их вероятности: р(А)=0,5, р(В)=0,4, р(С)=0,7. Укажите соответствие между событиями и их вероятностями:
1.
2.
3.
4.
1. 0,2
2. 0,35
4. 0,14
3. 0,28
- 0,9
Бросают три кубика. Вероятность появления трёх одинаковых чисел равна…
+ 1/36
- 1/216
- 1/6
- 4/9
Бросают три кубика. Вероятность появления трёх четных чисел равна…
- 1/216
+ 1/8
- 1/6
- 1/9
Бросают три кубика. Вероятность появления трёх нечетных чисел равна…
+ 1/8
- 1/36
- 1/6
- 1/9
В урне 8 шаров, из них 3 красных. Наудачу берут два шара. Тогда вероятность того, что среди них ровно один красный шар, равна…
- 1/15
+ 15/28
- 1/4
- 15/56
В урне находится 2 белых и 3 черных шара. Из урны поочередно вынимают два шара. Тогда вероятность того, что оба шара белые равна …
+ 1/10
- 1/20
- 4/25
- 13/20
В урне находится 5 белых и 3 черных шара. Из урны вынимают четыре шара. Тогда вероятность того, что два шара будут белые, а два - черные равна …
- 3/8
- 5/8
+ 3/7
- 1/14
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна...
- 0,9
+ 0,2
- 0,16
- 0,3
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,4 соответственно. Тогда вероятность того, что в цель не попадут оба стрелка, равна...
- 0,9
- 0,2
- 0,16
+ 0,3
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,4 соответственно. Тогда вероятность того, что в цель попадет первый и не попадет второй стрелок, равна...
- 0,9
- 0,2
- 0,16
+ 0,3
Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет четное число очков, равна...
+ 
- 
- 
- 
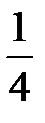
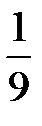
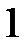
Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет четное число очков, большее 6, равна...
+ 
-
- 
- 
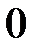
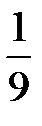
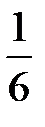
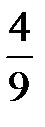
Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет четное число очков, не меньшее 3, равна...
-
+
-
-
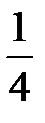
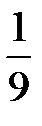
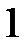
По мишени производится три выстрела. Значение вероятности ни одного попадания при всех трех выстрелах равно 0,5; значение вероятности ровно одного попадания – 0,3; значение вероятности ровно двух попаданий – 0,15. Тогда вероятность того, что мишень будет поражена не более одного раза, равна …
- 0,9
+ 0,8
- 0,15
- 0,3
На пути движения автомобиля находится три 3 светофора. Каждый из них разрешает дальнейшее движение с вероятностью 3/4 и запрещает с вероятностью 1/4. Тогда вероятность того, что хотя бы перед одним светофором автомобиль сделает остановку, равна …
- 1/64
- 1/3
+ 37/64
- 1
В лотерее 1000 билетов. На один билет выпадает выигрыш 5000 рублей, на десять билетов – выигрыши по 1000 рублей, на пятьдесят билетов – выигрыши по 50 рублей, остальные билеты проигрышные. Покупается один билет. Тогда вероятность выигрыша 250 рублей равна …
- 15/839
+ 0
- 0,15
- 1
В урне находится 2 белых и 6 черных шара. Из урны поочередно вынимают два шара, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются. Тогда вероятность того, что оба шара черные равна …
+ 9/16
- 1/64
- 10/35
- 1/9
В урне находится 2 белых и 6 черных шара. Из урны поочередно вынимают два шара, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются. Тогда вероятность того, что оба шара белые равна …
- 9/16
+ 1/16
- 10/35
- 1/9
В урне находится 2 белых и 4 черных шара. Из урны поочередно вынимают два шара, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются. Тогда вероятность того, что оба шара черные равна …
- 9/16
- 1/64
- 1/35
+ 4/9
Установите соответствие формулировки теоремы и формулы:
1. Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий.
2. Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже произошло
3. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
4. Вероятностью сложения двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
1. 
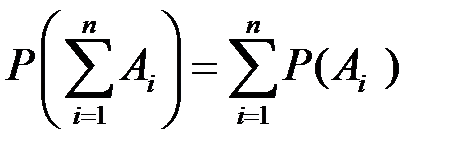
2. 
3. 
4. 
- 
Если некоторое событие А совершается с одним из n несовместных событий 
, образующих полную группу событий, то для определения вероятности этого события может быть использована формула…
- Бернулли
- Пуассона
- Муавра-Лапласа
+ полной вероятности,
- Байеса
Для определения вероятности события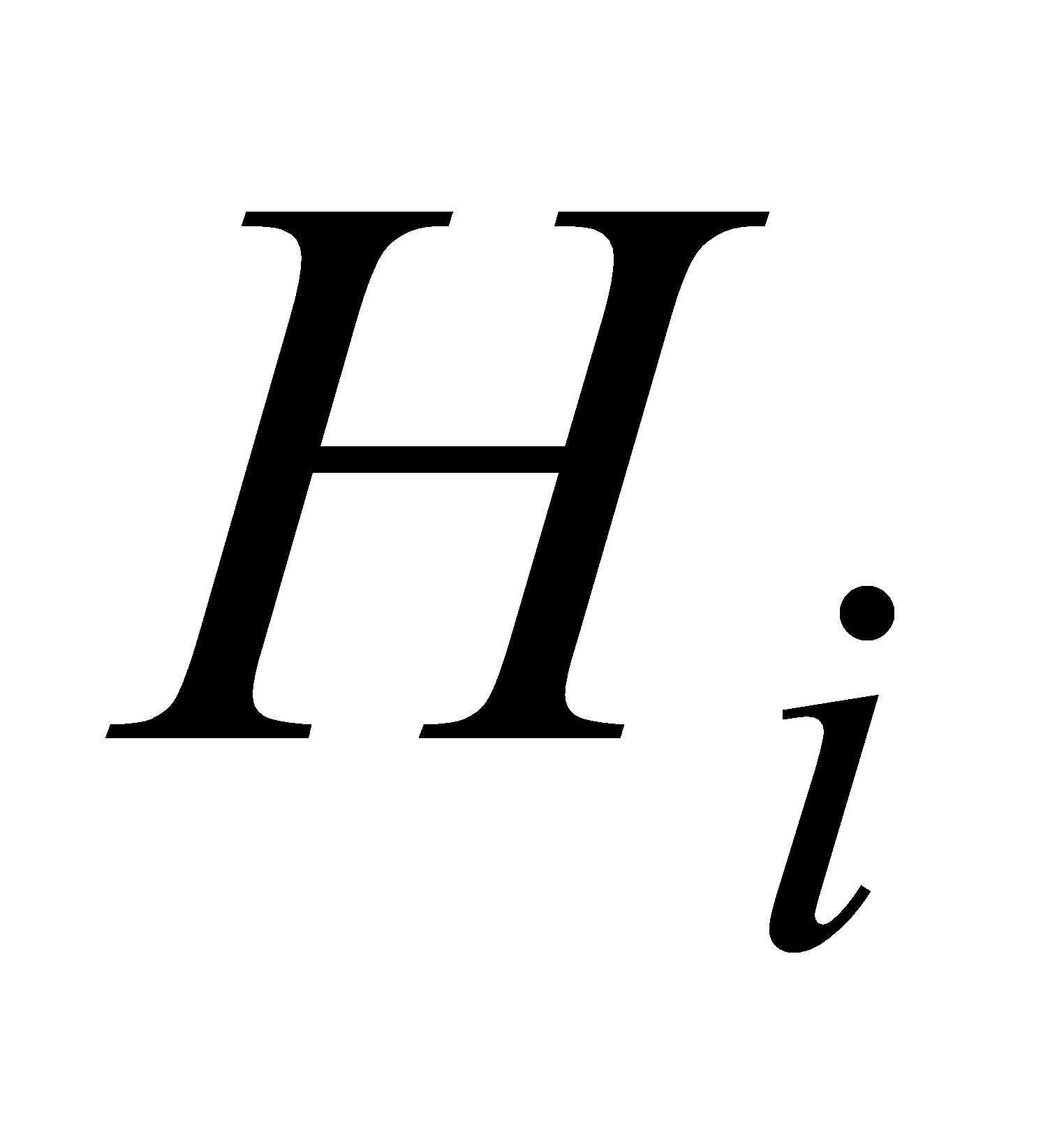 
при условии, что произошло событие А, используется формула
- Бернулли
- Пуассона
- Муавра-Лапласа
- полной вероятности,
+ Байеса
В первом ящике 7 красных и 11 синих шаров, во втором – 5 красных и 9 синих. Из произвольного ящика достают один шар. Вероятность того, что этот шар синий, равна …
- 
+ 
- 
- 
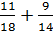
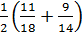
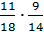
В первом ящике 12 черных и 5 белых шаров, во втором – 10 черных и 7 белых. Из произвольного ящика достают один шар. Вероятность того, что он белый, равна …
- 
- 
+ 
- 
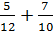
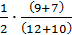
В первом ящике 2 черных и 8 белых шаров, во втором – 5 черных и 5 белых. Из произвольного ящика достают один шар. Вероятность того, что он черный, равна …
- 0,4
- 0,15
- 0,7
+ 0,35
Событие А может наступить лишь при условии появления одного из двух несовместных событий В1 и В2, образующих полную группу событий. Известны вероятности Р(В1)=1/6 и условные вероятности Р(А/В1)=2/3, Р(А/В2)=1/3. Тогда вероятность Р(А) равна …
- 11/18
- 5/6
- 2/3
+ 7/18
Событие А может наступить лишь при условии появления одного из двух несовместных событий В1 и В2, образующих полную группу событий. Известны вероятности Р(В1)=3/4 и условные вероятности Р(А/В1)=1/4, Р(А/В2)=1/2. Тогда вероятность Р(А) равна …
- 1/4
- 3/4
+ 5/16
- 3/16
Событие А может наступить лишь при условии появления одного из двух несовместных событий В1 и В2, образующих полную группу событий. Известны вероятности Р(В1)=1/5 и условные вероятности Р(А/В1)=1/3, Р(А/В2)=1/2. Тогда вероятность Р(А) равна …
+ 7/15
- 3/4
- 5/16
- 3/16
С первого станка на сборку поступает 20%, со второго – 80% всех деталей. Среди деталей первого станка 85% стандартных, второго – 95%. Наудачу взятая деталь оказалась нестандартной. Тогда вероятность того, что поступила на сборку со второго станка, равна...
- 
+ 
- 
- 
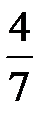
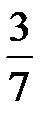
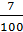
В ящике содержится 20 деталей, изготовленных на заводе №1, 30 деталей на заводе №2 и 50 деталей изготовленных на заводе №3. Вероятность того, что деталь, изготовленная на заводе №1, отличного качества, равна 0,8; на заводе №2 – равна 0,7, а на заводе №3 – равна 0,9. Тогда вероятность того, что наудачу извлеченная деталь окажется отличного качества, равна...
- 0,8
- 0,92
- 0,81
+ 0,82
Три организации представили в управление счета для выборочной проверки: первая – 15 счетов, вторая – 10, третья – 25. Вероятность правильного оформления счетов у этих организаций соответственно таковы: 0,9; 0,8; 0,7. Был выбран один счет, и он оказался правильным. Определить вероятность того, что этот счет принадлежит второй организации.
- 5/11
+ 8/39
- 7/20
- 7/11
Повторные испытания
Установите соответствие между названием и формулой
1. Формула Бернулли
2. Формула Пуассона
3. Локальная формула Муавра-Лапласа
4. Интегральная формула Муавра-Лапласа
1. 
2. 
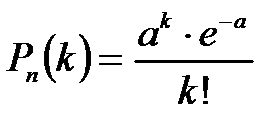
3. 
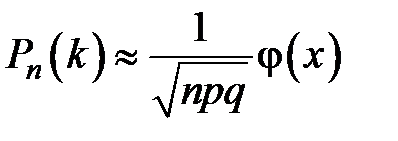
4. 
- 
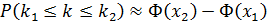
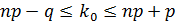
Вероятность того, что дом может сгореть в течение года, равна 0,01. Застраховано 500 домов. Для вычисления вероятности того, что сгорит не более 6 домов, следует использовать…
+ формулу Пуассона
- интегральную теорему Муавра - Лапласа
- локальную теорему Муавра - Лапласа
- формулу Бернулли
Вероятность попадания в мишень при одном выстреле для данного стрелка 0,7 и не зависит от номера выстрела. Для вычисления вероятности того, что при 5 выстрелах произойдет ровно 2 попадания, следует использовать…
- формулу Пуассона
- интегральную теорему Муавра - Лапласа
- локальную теорему Муавра - Лапласа
+ формулу Бернулли
Вероятность безотказной работы в течение недели каждого из автобусов данного автопарка равна 0,8. Для вычисления вероятности того, что среди 100 наудачу выбранных для проверки автобусов безотказно работали в течение недели от 65 до 90 автомобилей, следует использовать…
- формулу Пуассона
+ интегральную теорему Муавра - Лапласа
- локальную теорему Муавра - Лапласа
- формулу Бернулли
Вероятность наступления события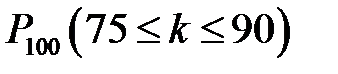 
при р=0,8 следует вычислять по формуле
- Пуассона
+ интегральной теореме Муавра - Лапласа
- локальной теореме Муавра - Лапласа
- Бернулли
Вероятность наступления события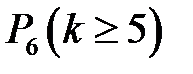 
при р=0,9 следует вычислять по формуле
- Пуассона
- интегральной теореме Муавра - Лапласа
- локальной теореме Муавра - Лапласа
+ Бернулли
Вероятность наступления события 
при р=0,36 следует вычислять по формуле
- Пуассона
- интегральной теореме Муавра - Лапласа
+ локальной теореме Муавра - Лапласа
- Бернулли
Всхожесть семян огурцов равна 0,8. Для вычисления вероятности того, что из пяти посаженных семян взойдут не менее четырех, следует использовать …
+
-
-
-
-
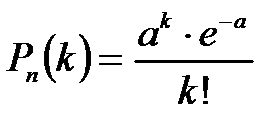
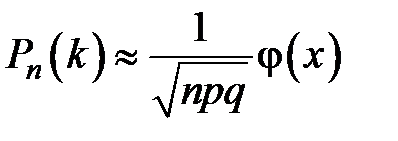
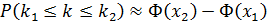
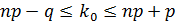
Завод отправил в торговую сеть 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Для вычисления вероятности того, что при транспортировке будет повреждено более трех изделий, следует использовать …
-
+
-
-
-
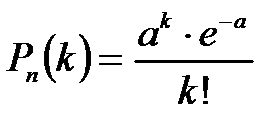
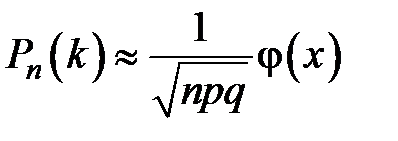
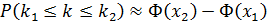
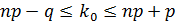
Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна 0,8. Для вычисления вероятности того, что событие появится не менее 70 раз, следует использовать…
-
-
-
+
-
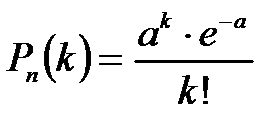
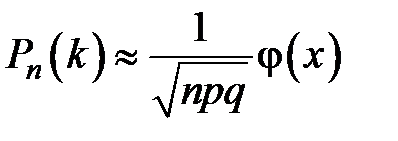
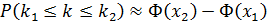
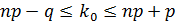
Вероятность наступления события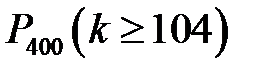 
при р=0,2 следует вычислять по формуле
-
-
-
+
-
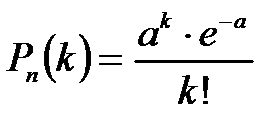
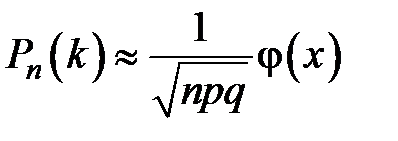
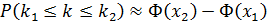
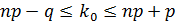
Вероятность наступления события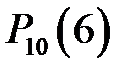 
при р=0,3 следует вычислять по формуле
+
-
-
-
-
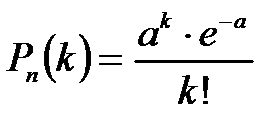
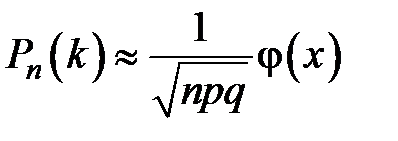
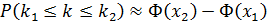
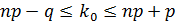
Вероятность наступления события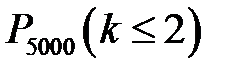 
при р=0,003 следует вычислять по формуле
-
+
-
-
-
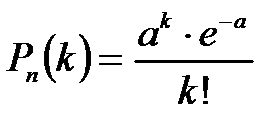
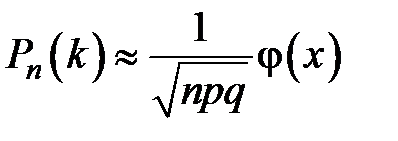
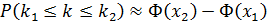
