—лучайна€ величина, котора€ принимает отдельные, изолированные возможные значени€ с определенными веро€тност€ми называетс€ Е
+ дискретна€ случайна€ величина
- непрерывна€ случайна€ величина
- дисперси€
- закон распределени€
- функци€ распределени€
—оответствие между возможными значени€ми и их веро€тност€ми дискретной случайной величины называетс€ ее Е
- средним квадратическим отклонением
- математическим ожиданием
- дисперсией
+ законом распределени€
- функцией распределени€
—умма произведений всех возможных значений дискретной случайной величины на соответствующие веро€тности называетс€ Е
- средним квадратическим отклонением
+ математическим ожиданием
- дисперсией
- законом распределени€
- функцией распределени€
ћатематическое ожидание квадрата отклонени€ дискретной случайной величины от ее математического ожидани€ называетс€ Е
- дискретной случайной величиной
- математическим ожиданием
+ дисперсией
- законом распределени€
- функцией распределени€
‘ункци€, определ€юща€ веро€тность того, что случайна€ величина ’, в результате испытани€ примет значение, меньшее, чем х, называетс€ Е
- дискретна€ случайна€ величина
- математическое ожидание
- дисперси€
- закон распределени€
+ функци€ распределени€
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей
| ’ | -1 | |||
| – | 0,2 | 0,3 | 0,1 | 0,4 |
“огда значение интегральной функции распределени€ веро€тностей F(2) равно...
- 0,5
- 1
+ 0,6
- 0,4
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей
| ’ | -1 | |||
| – | 0,2 | 0,3 | 0,1 | 0,4 |
“огда значение интегральной функции распределени€ веро€тностей F(0,5) равно...
+ 0,5
- 1
- 0,6
- 0,4
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей
| ’ | -1 | |||
| – | 0,2 | 0,3 | 0,1 | 0,4 |
“огда значение интегральной функции распределени€ веро€тностей F(-0,5) равно...
- 0,5
- 1
+ 0,2
- 0,4
‘ункци€ распределени€ веро€тностей дискретной случайной величины ’ имеет вид

“огда веро€тность  равна Е
равна Е
- 0,5
+ 0,3
- 0,4
- 0,6
‘ункци€ распределени€ веро€тностей дискретной случайной величины ’ имеет вид

“огда веро€тность  равна Е
равна Е
- 0,5
- 0,3
+ 0,4
- 0,7
‘ункци€ распределени€ веро€тностей дискретной случайной величины ’ имеет вид

“огда веро€тность  равна Е
равна Е
- 0,5
- 0,3
- 0,4
+ 0,2
«адан закон распределени€ дискретной случайной величины
| ’ | |||||
| – | 0,1 | р | 0,35 | 0,35 | 0,1 |
“огда значение р равнаЕ
+ 1/10
- 1/4
- 1/2
- 1/5
«адан закон распределени€ дискретной случайной величины
| ’ | ||||
| р | 0,2 | 0,3 | р | 0,1 |
“огда значение р равноЕ
|
|
|
+ 0,4
- 0,6
- 0,3
- 0,9
«адан закон распределени€ дискретной случайной величины
| ’ | ||||
| р | 0,1 | 0,2 | р | 0,5 |
“огда значение р равноЕ
- 0,4
- 0,5
- 0,3
+ 0,2
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей:
| ’ | |||
| р | 0,3 | 0,3 | 0,4 |
“огда ее функци€ распределени€ веро€тностей имеет вид Е
- 
- 
+ 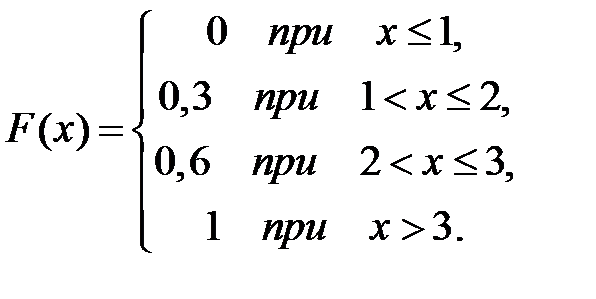
- 
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей:
| ’ | |||
| р | 0,2 | 0,5 | 0,3 |
“огда ее функци€ распределени€ веро€тностей имеет вид Е
- 
- 
- 
+ 
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей:
| ’ | |||
| р | 0,5 | 0,3 | 0,2 |
“огда ее функци€ распределени€ веро€тностей имеет вид Е
- 
- 
+ 
- 
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей:
| ’ | ||||
| р | 0,1 | a | b | 0,3 |
“огда значени€ a и b могут быть равны Е
- a=0,6, b=0,6
- a=0,3, b=0,2
- a=0,3, b=0,1
+ a=0,4, b=0,2
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей:
| ’ | ||||
| р | 0,2 | a | b | 0,3 |
“огда значени€ a и b могут быть равны Е
- a=0,5, b=0,5
+ a=0,3, b=0,2
- a=0,3, b=0,1
- a=0,4, b=0,2
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей:
| ’ | ||||
| р | 0,4 | a | b | 0,3 |
“огда значени€ a и b могут быть равны Е
- a=0,7, b=0,7
- a=0,3, b=0,2
+ a=0,2, b=0,1
- a=0,4, b=0,3
≈сли к случайной величине ’ прибавить посто€нную величину  , то
, то 
- не изменитс€
+ увеличитс€ на  единиц
единиц
- увеличитс€ в  единиц
единиц
- увеличитс€ на  единиц
единиц
≈сли к случайной величине ’ прибавить посто€нную величину  , то
, то 
+ не изменитс€
- увеличитс€ на  единиц
единиц
- увеличитс€ в  единиц
единиц
- увеличитс€ на  единиц
единиц
≈сли к случайной величине ’ прибавить посто€нную величину  , то
, то 
+ не изменитс€
- увеличитс€ на  единиц
единиц
- увеличитс€ в  единиц
единиц
- увеличитс€ на  единиц
единиц
≈сли случайную величину ’ умножить на посто€нную величину  , то
, то 
- не изменитс€
- увеличитс€ на  единиц
единиц
+ увеличитс€ в  единиц
единиц
- увеличитс€ на  единиц
единиц
≈сли случайную величину ’ умножить на посто€нную величину  , то
, то 
- не изменитс€
- увеличитс€ на  единиц
единиц
- увеличитс€ в  единиц
единиц
+ увеличитс€ в  единиц
единиц
≈сли случайную величину ’ умножить на посто€нную величину  , то
, то 
- не изменитс€
- увеличитс€ на  единиц
единиц
+ увеличитс€ в  единиц
единиц
- увеличитс€ на  единиц
единиц
≈сли ’ Ц число по€влений событи€ ј в 10 испытани€х, где р(ј) = р= 0,6 то ћ(’) и D(’) принимают значени€Е
- ћ(’) =0, D(’) =1,2
- ћ(’) =3, D(’) =1,6
- ћ(’) =4, D(’) =1,2
+ ћ(’) =6, D(’) =2,4
≈сли ’ - число по€влений событи€ ј в 12 испытани€х, где р(ј) = р= 0,4, то ћ(’) и D(’) принимают значени€
- ћ(’) =6,1, D(’) =4,34
+ ћ(’)= 4,8, D(’) =2,88
- ћ(’)= 3,8, D(’) =2,79
- ћ(’) =5,6, D(’) =3,66
≈сли ’ - число по€влений событи€ ј в 14 испытани€х, где р(ј) = р= 0,7, то ћ(’) и D(’) принимают значени€
|
|
|
- ћ(’) =6,4, D(’) =5,04
- ћ(’)= 5,2, D(’) =2,12
+ ћ(’)= 9,8, D(’) =2,94
- ћ(’) =2,6, D(’) =1,52
ƒискретна€ случайна€ величина ’ имеет закон распределени€ веро€тностей:
| ’ | ||
| р | 0,3 | 0,7 |
ћатематическое ожидание этой случайной величины равноЕ
- 1
- 5
+ 2,7
- 2,3
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей:
| ’ | -1 | |
| – | 0,1 | 0,9 |
“огда математическое ожидание этой случайной величины равно...
+ 4,4
- 4,5
- 4,6
- 2
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей:
| ’ | -1 | |
| – | 0,4 | 0,6 |
“огда математическое ожидание этой случайной величины равно...
+ 2
- 1,5
- 3
- 2,8
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей
| ’ | -1 | ||
| р | 0,1 | 0,3 | 0,6 |
“огда математическое ожидание случайной величины Y=4X равноЕ
- 4
+ 4,4
- 5,2
- 5,1
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей
| ’ | -1 | ||
| р | 0,1 | 0,3 | 0,6 |
“огда математическое ожидание случайной величины Y=6X равноЕ
- 18,6
- 8,9
+ 17,4
- 24
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей
| ’ | -1 | ||
| р | 0,1 | 0,3 | 0,6 |
“огда математическое ожидание случайной величины Y=3X равноЕ
- 7,5
- 9
- 5,3
+ 6,9
¬еро€тность по€влени€ событи€ ј в 20 независимых испытани€х, проводимых по схеме Ѕернулли, равна 0,54. “огда математическое ожидание числа по€влений этого событи€ равно Е
- 9,20
- 4,97
- 10,26
+ 10,8
¬еро€тность по€влени€ событи€ ј в 30 независимых испытани€х, проводимых по схеме Ѕернулли, равна 0,24. “огда математическое ожидание числа по€влений этого событи€ равно Е
- 9,20
+ 7,2
- 7,5
- 10,8
¬еро€тность по€влени€ событи€ ј в 20 независимых испытани€х, проводимых по схеме Ѕернулли, равна 0,36. “огда математическое ожидание числа по€влений этого событи€ равно Е
- 10,20
- 7,4
- 10,26
+ 7,2
≈сли ’ и Y случайные величины, D(’)=1, D(Y)=2, а Z= 6 ’+ 3 Y, то D(Z) равнаЕ
- 12
+ 54
- 42
- 24
≈сли ’ и Y случайные величины, ћ (’)=2, ћ (Y)=3, а Z= 7 ’+ 4 Y, то ћ(Z) равнаЕ
+ 26
- 146
- 13
- 5
≈сли ’ и Y, случайные величины, D (’)=2, D (Y)=3, а Z= 6 ’- 3 Y, тогда D(Z) равнаЕ
- 3
- 45
- 21
+ 99
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей:
| ’ | х2 | ||
| р | 0,2 | 0,6 | 0,2 |
≈сли математическое ожидание ћ(’)= 3,6, то значение х2 равно Е
- 4
+ 3
- 5
- 6
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей:
| ’ | х1 | ||
| р | 0,3 | 0,4 | 0,3 |
≈сли математическое ожидание ћ(’)= 3,2, то значение х1 равно Е
- 1
- Ц1
- 0
+ Ц2
ƒискретна€ случайна€ величина ’ задана законом распределени€ веро€тностей:
| ’ | х3 | ||
| р | 0,5 | 0,1 | 0,4 |
≈сли математическое ожидание ћ(’)= 3,4, то значение х3 равно Е
- 10
- 7
+ 5
- 6






