Формула класичної ймовірності

 

Теорія ймовірностей має ряд основних первинних понять, на яких базуються всі теоретичні побудови і висновки. До них належать: стохастичний експеримент, випадкова подія, ймовірність, випадкова величина.

Стохастичним експериментом називається експеримент, який можна неодноразово повторювати за деяких незмінних умов і результат якого неможливо передбачити заздалегідь. Подія – це будь-який результат експерименту. Елементарні події – це єдино можливі результати експерименту, що є взаємно виключні. Події бувають випадкові, неможливі, достовірні. Достовірною називають подію Ω, що обов’язково відбудеться, якщо буде здійснена сукупність відповідних умов .

Неможливою називається подія Ø,яка свідомо не відбудеться, якщо буде здійснена сукупність умов .

Подія називається випадковою, якщо реалізація сукупності відповідних умов може мати принаймні два наслідки.

Ймовірність в загальному випадку є кількісна міра можливості появи події в експерименті. Позначимо ймовірність події 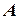буквою 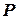(probability (англ.) – ймовірність).

Ймовірністю події 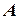називають відношення кількості сприяючих події 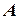результатів експерименту 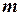до загальної кількості рівноможливих несумісних елементарних подій 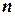, тобто

 

, .

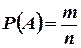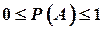Теореми додавання ймовірностей

сумісних подій

;

несумісних подій

.

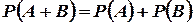Наслідок 1. Сума ймовірностей подій 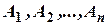, що складають повну групу, дорівнює одиниці, тобто

.

Наслідок 2. Сума ймовірностей протилежних подій дорівнює одиниці, тобто

.

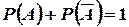Подія 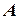називається незалежною від події 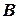, якщо ймовірність здійснення події 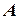не залежить від того, відбулася або ні подія 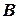(у протилежному випадку події залежні).

Ймовірність 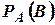або називається умовною ймовірністю події 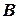за умови 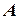, тобто це ймовірність настання події 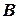, обчислена в припущенні, що подія 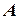вже відбулася.

Теорема множення ймовірностей

незалежних подій

;

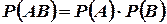залежних подій

.

 

Ймовірність появи хоча б однієї з незалежних в сукупності подій дорівнює різниці між одиницею та добутком ймовірностей протилежних подій, тобто

 

.

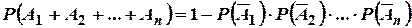Задача 1. Кидають два гральних кубика. Яка ймовірність того, що сума очок, що випали, буде парною?

Розв’язання. Позначимо через А подію, ймовірність якої треба знайти. За означенням, ймовірність 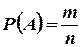. Кількість усіх можливих комбінацій, що взагалі можуть бути у цьому випадку .

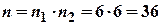Події А будуть сприяти 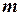= 18 комбінацій, у яких сума очок буде парною, а саме: 1-1, 1-3, 1-5, 2-2, 2-4, 2-6, 3-1, 3-3, 3-5, 4-2, 4-4, 4-6, 5-1, 5-3, 5-5, 6-2, 6-4, 6-6.

Таким чином,

.

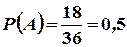Задача 2. В урні містяться 6 білих і 4 чорних кульки. З урни виймають навмання одразу 5 кульок. Знайти ймовірність події: А – усі кульки білі; В – чотири кульки білі та одна чорна.

Розв’язання. Число рівноможливих незалежних подій дорівнює

.

Події А сприяють 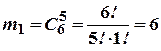, а події В – 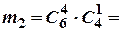= 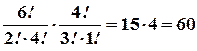наслідків експерименту. Тому

,

.

 

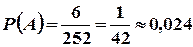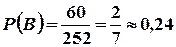Задача 3. У коробці містяться шість однакових, занумерованих кульок. Навмання по одній виймають усі кульки. Знайти ймовірність того, що номери вийнятих кульок розташуються за зростанням.

Розв’язання. Нехай А – подія, ймовірність якої треба знайти. Результатами експерименту є перестановки без повторень з 6 елементів. Число усіх результатів експерименту дорівнює 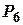. Для події А сприятливим є лише один результат (номери зростатимуть). Отже,

 

.

 

Задача 4. Слово “інтеграл” складено з літер на картках розрізної азбуки. З них навмання виймають три картки і кладуть в ряд одну за однією в порядку появи. Яка ймовірність того, що при цьому складеться слово “гра”?

Розв’язання. При утворенні простору елементарних подій розглядуються усі впорядковані 3-елементні підмножини 8-елементної множини (букви, що утворюють слово “інтеграл”). Тому 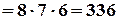, а сприятливими для шуканої події А є лише один випадок , коли підряд буде вийнято букви “г”, “р” і “а”. Отже,

 

.

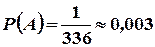Задача 5. Ймовірність попадання в мішень одним стрільцем становить 0,8, іншим – 0,7. Стрільці незалежно один від одного зробили по одному пострілу. Яка ймовірність того, що принаймні один стрілець влучить в мішень?

Розв’язання. Нехай подія А – влучення першого стрільця в ціль, подія В – другого, а подія С – шукана подія. Тоді С=А+В. Враховуючи, що події А і В – сумісні, проте незалежні, дістаємо:

 

 

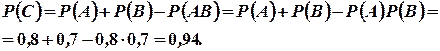
Задача 6. У дівчинки є 3 в клітинку та 7 в лінійку зошитів. Вона бере один раз 2 зошити, а потім ще 2. Яка ймовірність того, що взяті зошити в лінійку?

Розв’язання. Нехай подія А полягає в тому, що перший раз взяті зошити в лінійку, подія В – другий раз взяті теж зошити в лінійку.

Оскільки події А й В залежні, то за теоремою добутку ймовірностей залежних подій

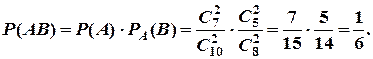
Задача 7. Стрілець 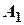влучає в ціль з ймовірністю , стрілець 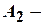з ймовірністю 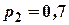, стрілець 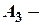з ймовірністю . Знайти ймовірність хоча б одного попадання (подія А) при одному пострілі кожного зі стрільців.

Розв’язання. Обчислимо ймовірності протилежних подій, які полягають в тому, що кожен зі стрільців не влучить в ціль:

; ; .

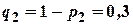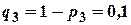Ймовірність того, що жоден зі стрільців не влучить в ціль, тобто ймовірність події дорівнює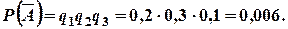

Тоді ймовірність того, що хоча б один зі стрільців влучить в ціль

.
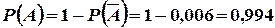