Основною задачею в диференціальних рівняннях є знаходження їхнього загального розв’язку. Ця задача найповніше вивчена для лінійних рівнянь із сталими коефіцієнтами.
Лінійні однорідні рівняння другого порядку із сталими коефіцієнтами.
Розглянемо лінійне однорідне рівняння другого порядку
(1)
де 
дійсні числа.
Ейлер запропонував шукати частинні розв’язки цього рівняння у вигляді 
, де 
– стала (дійсна чи комплексна), яку треба знайти. Підставивши функцію 
в рівняння 1, дістанемо
Оскільки 
то
(2)
Отже, якщо 
буде коренем рівняння 2, то функція 
буде розв’язком рівняння 1. Квадратне рівняння 2 називається характеристичним рівнянням диференціального рівняння 1.
Позначимо корені характеристичного рівняння через 
можливі три випадки:
І. 
і 
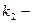дійсні і різні числа 
ІІ. і 
комплексні числа 
;
ІІІ. і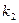 
- дійсні і рівні числа 
.
Розглянемо кожен випадок окремо.
І. Корені характеристичного рівняння дійсні і різні: 
. У цьому випадку частинними розв’язками рівняння 1 є функції 
Ці розв’язки лінійно незалежні, тому що при
.
Загальний розв’язок рівняння 1 знаходять за формулою 
. (3)
ІІ. Корені характеристичного рівняння комплексно – спряжені:
Підставивши значення 
та 
у формулу 
,знайдемо розв’язки
За формулою Ейлера
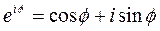
маємо
Зауважимо,що коли функція 
є розв’язком рівняння 1, то розв’язками будуть також функції 
та 
. Дійсно, підставивши функції 
в рівняння 1, дістанемо:
або
Остання тотожність можлива, коли вирази в дужках дорівнюють нулю. Це означає, що функції 
та 
- розв’язки рівняння 1. Згідно з цим зауваженням частинними розв’язками рівняння 1 є функції 
.
Ці розв’язки лінійно незалежні, оскільки
тому загальний розв’язок рівняння 1 запишеться у вигляді
(4)
ІІІ. Корені характеристичного рівняння дійсні і рівні: 
За формулою 
дістанемо один з розв’язків: 
.
Другий розв’язок шукатимемо у вигляді 
де 
невідома функція від 
. Знайшовши 
та підставивши їх у рівняння 1 дістанемо:
або
Оскільки 
- корінь рівняння 2, то 
і за теоремою Вієта 
, тому 
і 
звідки 
де 
довільні сталі. Поклавши 
(нас цікавить розв’язок 
), знайдемо другий частинний розв’язок рівняння 1:
Розв’язки 
- лінійно незалежні, тому загальний розв’язок рівняння 1 має вигляд:
. (5)
Приклад 1.
Розв’язати рівняння: 
.
Розв’язання:
Складемо характеристичне рівняння 
і знайдемо його корені 
за формулою 
шуканий розв’язок має вигляд:
.
Приклад 2.
Розв’язати рівняння: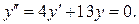 
Розв’язання:
Характеристичне рівняння 
має комплексні корені 
Загальний розв’язок дістанемо за формулою (4):
.
Приклад 3.
Розв’язати рівняння: y ²+2 y ¢+ y =0.
Розв’язання:
Будуємо характеристичне рівняння 
, звідки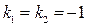 
.
Отже, загальний розв’язок: 
.
