Комбінаторика вивчає методи підрахунку кількості комбінацій, підкорених певним умовам, які можна утворити з елементів заданої скінченої множини будь-якого походження.
Групи елементів, які відрізняються порядком або складом елементів, називаються сполуками. Вони бувають трьох типів: розміщення, перестановки, комбінації.
Розміщення
Розміщеннями з n елементів по 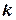 називаються будь-які впорядковані
називаються будь-які впорядковані 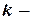 елементні підмножини n -елементної множини, що різняться одна від одної або своїми елементами, або їхнім порядком (якщо вибрані елементи не повторюються, то маємо розміщення без повторень, а якщо повторюються – розміщення з повтореннями).
елементні підмножини n -елементної множини, що різняться одна від одної або своїми елементами, або їхнім порядком (якщо вибрані елементи не повторюються, то маємо розміщення без повторень, а якщо повторюються – розміщення з повтореннями).
Формули для числа розміщень 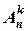
| Без повторень | З повтореннями |

| 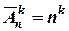
|
Приклад. Кількість різних тризначних телефонних номерів, які можна скласти з цифр від 0 до 9 так, щоб у запису номера всі цифри були різні, 
| Приклад. Кількість різних тризначних телефонних номерів, які можна скласти з цифр від 0 до 9, якщо цифри в числі можуть повторюватися,
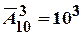
|
Перестановками k -елементної множини називаються її k -елементні впорядковані підмножини, що відрізняються тільки порядком елементів (якщо всі елементи заданої множини різні – маємо перестановки без повторень, а якщо в заданій множині елементи можуть повторюватися, серед яких 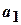 повторюється
повторюється  раз,
раз, 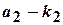 разів, …,
разів, …, 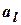 –
–  разів, то маємо перестановки з повтореннями).
разів, то маємо перестановки з повтореннями).
Формули для числа перестановок 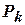
| Без повторень | З повтореннями |
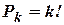
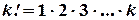

| 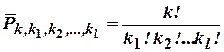 де
де 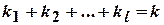
|
Приклад. Скільки різних шестизначних чисел можна скласти з цифр 1, 2, 3, 4, 5, 6, не повторюючи ці цифри в одному числі?
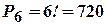
| Приклад. Скількома способами можна переставити букви у слові “математика”?
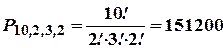
|
Комбінації (сполучення)
Комбінаціями (сполученнями) без повторень з n елементів по 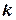 називаються будь-які k -елементні підмножини n -елементної множини, що різняться між собою принаймні одним елементом. Порядок елементів у сполученні не є істотним.
називаються будь-які k -елементні підмножини n -елементної множини, що різняться між собою принаймні одним елементом. Порядок елементів у сполученні не є істотним.
Комбінаціями (сполученнями) з повтореннями з n елементів (необов’язково різних) по 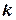 називаються набори цих елементів, до кожного з яких входять
називаються набори цих елементів, до кожного з яких входять 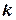 елементів і які відрізняються хоча б одним елементом або тим, що принаймні один елемент входить в різні сполучення різне число разів.
елементів і які відрізняються хоча б одним елементом або тим, що принаймні один елемент входить в різні сполучення різне число разів.
Формули для числа комбінацій (сполучень) 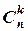
| Без повторень | З повтореннями |
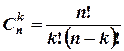 , , 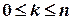
| 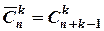
|
Приклад. З групи, що складається з 25 студентів, можна виділити 5 осіб для чергування по академії 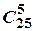 способами, тобто способами, тобто
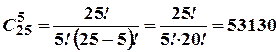 . .
| Приклад. Якщо у продажу є квіти чотирьох сортів, то різних букетів, що складаються з 7 квіток, можна скласти
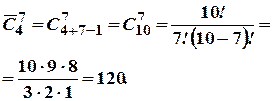
|
Деякі властивості числа сполучень (без повторень):
1. 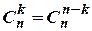 (зокрема,
(зокрема, 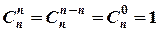 ).
).
2. 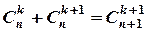 .
.
3. 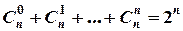 .
.
Зауваження. Розміщення, перестановки та сполучення пов’язані між собою рівністю
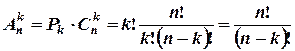 .
.
Правило множення. Нехай необхідно виконати одну за одною 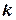 дій. Якщо першу дію можна виконати
дій. Якщо першу дію можна виконати 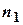 числом способів, другу -
числом способів, другу - 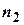 числом способів і так до
числом способів і так до 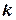 -ї дії, яку можна виконати
-ї дії, яку можна виконати 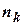 числом способів, то всі
числом способів, то всі 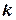 дій разом можуть бути виконані
дій разом можуть бути виконані 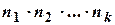 числом способів.
числом способів.




