Основные определения, свойства пределов функций одной переменной
Основные определения
Понятие предела функции является одним из основных в математическом анализе. Определения производной, интеграла, непрерывности и т.д. основаны на использовании предела.
Число b называют пределом функции  при
при  , если для любого числа
, если для любого числа  найдется такое число
найдется такое число 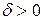 , что при всех х, удовлетворяющих условию
, что при всех х, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство  . Предел функции f (x) при x, стремящемся к а, обозначают
. Предел функции f (x) при x, стремящемся к а, обозначают  либо
либо  при
при  .
.
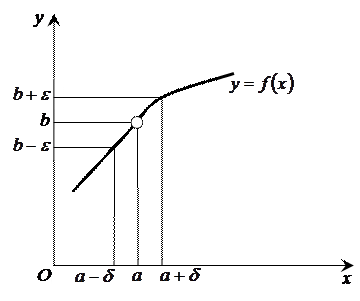 Дадим геометрическую интерпретацию понятия предела функции в точке. На рисунке изображен график функции
Дадим геометрическую интерпретацию понятия предела функции в точке. На рисунке изображен график функции  . Предположим, что функция имеет при
. Предположим, что функция имеет при  пределом число b. Возьмем произвольное сколь угодно малое число
пределом число b. Возьмем произвольное сколь угодно малое число  . Окружим число b
. Окружим число b  -окрестностью
-окрестностью  . Найдем на оси Ox такую окрестность точки a:
. Найдем на оси Ox такую окрестность точки a: 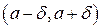 , при попадании в которую значений аргумента x соответствующие значения функции попадут в
, при попадании в которую значений аргумента x соответствующие значения функции попадут в  -окрестность числа b. При уменьшении числа
-окрестность числа b. При уменьшении числа  интервал
интервал  будет стягиваться к числу b. Соответствующий ему интервал
будет стягиваться к числу b. Соответствующий ему интервал 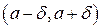 будет стягиваться к числу a. Это и доказывает, что
будет стягиваться к числу a. Это и доказывает, что  .
.
Число b называют пределом функции  при
при  или
или  , если для любого числа
, если для любого числа  можно указать положительное число N, такое, что при всех х, удовлетворяющих условию
можно указать положительное число N, такое, что при всех х, удовлетворяющих условию 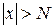 , выполняется неравенство
, выполняется неравенство  .
.
Свойства предела функции
1. Функция 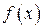 при
при  имеет единственный предел.
имеет единственный предел.
2. Предел постоянной равен самой постоянной: 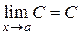
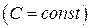 .
.
3. Постоянную можно выносить за знак предела  .
.
4. Предел суммы или разности конечного числа функций равен сумме или разности пределов этих функций  .
.
5. Предел произведения двух функций равен произведению пределов этих функций 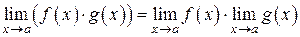 .
.
6. Предел частного двух функций равен частному пределов этих функций  при условии, что
при условии, что 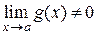 .
.
7. Если 
 , то
, то 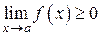
 .
.
8. Пусть функции связаны соотношением 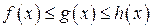 , причем
, причем 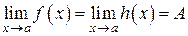 , тогда и
, тогда и  .
.
9.  .
.
Следствие.  .
.
10.  .
.
Замечание. Все свойства пределов распространяются и на случай, когда  .
.
Понятие неопределенностей
В практике отыскания пределов наиболее часто применяются свойства 2 - 6 об арифметических действиях над пределами. Однако их непосредственное применение бывает невозможно в особых случаях, называемых неопределенностями, которые возникают при нарушении их условий. Виды неопределенностей  ,
,  ,
,  ,
,  .
.
Кроме этих неопределенностей, связанных с арифметическими действиями над пределами, существуют неопределенности  ,
,  ,
,  .
.
Чтобы найти пределы при наличии неопределенности, надо эту неопределенность устранить, открыв тем самым возможность использования того или иного свойства пределов. Это достигается, с одной стороны, применением алгебраических и тригонометрических преобразований (разложение функции на множители или на слагаемые, приведение дробей к общему знаменателю, добавление и вычитание некоторого выражения, умножение и деление на некоторую функцию, вынесение множителя за скобку и т.п.) заменой переменной, использованием эквивалентных бесконечно малых и бесконечно больших, а с другой стороны, использование так называемых замечательных пределов.
Таблица раскрытия различных видов неопределенностей
| Тип неопределенности | Правило раскрытия |
1. 
| 1.1. Чтобы раскрыть неопределенность вида  , заданную отношением двух многочленов, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени. , заданную отношением двух многочленов, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени.
|
1.2. Для раскрытия неопределенности вида  , заданную отношением иррациональных функций, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени с учетом степеней корней. , заданную отношением иррациональных функций, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени с учетом степеней корней.
| |
2.
| 2.1. Для того, чтобы определить предел дробно-рациональной функции в случае, когда при  числитель и знаменатель дроби имеют пределы, равные нулю, надо числитель и знаменатель дроби разделить на числитель и знаменатель дроби имеют пределы, равные нулю, надо числитель и знаменатель дроби разделить на  и перейти к пределу. Если и после этого числитель и знаменатель новой дроби имеют пределы, равные нулю при и перейти к пределу. Если и после этого числитель и знаменатель новой дроби имеют пределы, равные нулю при  , то надо произвести повторное деление на , то надо произвести повторное деление на  . .
|
2.2. Чтобы раскрыть неопределенность вида  ,
в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности, умножив и числитель и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.
В случае квадратных корней и числитель и знаменатель дроби умножаются на сопряженное выражение тому, которое содержит иррациональность и применяется формула ,
в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности, умножив и числитель и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.
В случае квадратных корней и числитель и знаменатель дроби умножаются на сопряженное выражение тому, которое содержит иррациональность и применяется формула  .
В случае кубических корней и числитель и знаменатель дроби умножаются на неполный квадрат суммы или разности и применяется формула .
В случае кубических корней и числитель и знаменатель дроби умножаются на неполный квадрат суммы или разности и применяется формула  . .
| |
3. 
| 3.1. Неопределенность вида  ,
получающаяся в результате алгебраической суммы иррациональных выражений, устраняется или приводится к типу 1 путем домножения и деления на одно и то же выражение, приводящее к формулам сокращенного умножения.
В случае квадратных корней разность домножается на сопряженное выражение и применяется формула ,
получающаяся в результате алгебраической суммы иррациональных выражений, устраняется или приводится к типу 1 путем домножения и деления на одно и то же выражение, приводящее к формулам сокращенного умножения.
В случае квадратных корней разность домножается на сопряженное выражение и применяется формула  .
В случае кубических корней функция домножается на неполный квадрат суммы или разности и применяется формула .
В случае кубических корней функция домножается на неполный квадрат суммы или разности и применяется формула  . .
|
3.2. Неопределенность вида  ,
получающаяся в результате алгебраической суммы двух дробей, устраняется или сводится к типу 2 ,
получающаяся в результате алгебраической суммы двух дробей, устраняется или сводится к типу 2  путем приведения дробей к общему знаменателю.
Пусть путем приведения дробей к общему знаменателю.
Пусть  , , 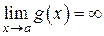 .
Тогда .
Тогда 

| |
| 4. Замечатель-ные пределы |
4.1. Первый замечательный предел
(неопределенность  ).
В случае, когда под знаком предела стоят тригонометрические функции, дающие неопределенность ).
В случае, когда под знаком предела стоят тригонометрические функции, дающие неопределенность  , используется первый замечательный предел: , используется первый замечательный предел:
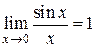 .
Его различные формы: .
Его различные формы: 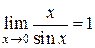 , ,
 , ,  , ,
 , ,  , ,
 , ,  . .
|
4.2. Второй замечательный предел
(неопределенность  ): ):
 .
Его различные формы: .
Его различные формы:  , ,
 , ,
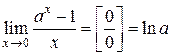 , ,
 , ,
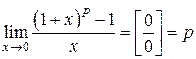 . .
| |
5.
| 5.1. Неопределенность типа  сводится либо к неопределенности типа 1
сводится либо к неопределенности типа 1  , либо к неопределенности типа 2 , либо к неопределенности типа 2  путем перемещения в знаменатель одного из сомножителей. Пусть путем перемещения в знаменатель одного из сомножителей. Пусть  , , 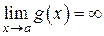 .
Тогда .
Тогда 
|
6.  , , 
| 6.1. Неопределенности вида  , ,  сводятся к неопределенности типа 5
сводятся к неопределенности типа 5  путем логарифмирования. путем логарифмирования.
|
Замечание.
Применение замечательных пределов требует понимания и запоминания структуры каждого из них и при необходимости ее воспроизведения. Так, для предела 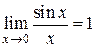 характерно отношение синуса бесконечно малого угла к самому углу. Поэтому всякий предел вида
характерно отношение синуса бесконечно малого угла к самому углу. Поэтому всякий предел вида  равен 1, если
равен 1, если  . Например, каждый из пределов
. Например, каждый из пределов 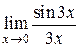 ,
,  ,
, 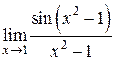 есть, в сущности, первый замечательный предел и потому равен 1, чего нельзя сказать ни об одном из пределов
есть, в сущности, первый замечательный предел и потому равен 1, чего нельзя сказать ни об одном из пределов  ,
,  ,
,  .
.
Для предела  (е - иррациональное число е =2,7182818…) характерно, что сумма, равная единице плюс бесконечно малая, возводится в степень, обратную этой бесконечно малой. Следовательно, если
(е - иррациональное число е =2,7182818…) характерно, что сумма, равная единице плюс бесконечно малая, возводится в степень, обратную этой бесконечно малой. Следовательно, если  , то и
, то и  . Такова структура каждого из пределов
. Такова структура каждого из пределов  ,
,  ,
,  , и поэтому все они равны e, но структура пределов
, и поэтому все они равны e, но структура пределов  ,
,  ,
,  отлична от структуры второго замечательного предела.
отлична от структуры второго замечательного предела.
Подобные рассуждения справедливы и для других форм замечательных пределов.
§3. Раскрытие неопределенностей вида 
Пример 1.
Вычислить предел функции  .
.
Решение. Знаменатель дроби  обращается в нуль при
обращается в нуль при  , а потому функция
, а потому функция  при
при  не существует. Теорему о пределе дроби применить нельзя, так как предел знаменателя равен нулю. Но определение предела функции содержит существенную оговорку: при отыскании предела функции
не существует. Теорему о пределе дроби применить нельзя, так как предел знаменателя равен нулю. Но определение предела функции содержит существенную оговорку: при отыскании предела функции  при
при  значение функции
значение функции  при
при  может не рассматриваться.
может не рассматриваться.
Т.к. при 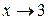 числитель и знаменатель дроби – бесконечно малые функции
числитель и знаменатель дроби – бесконечно малые функции  и
и  , то имеем неопределенность вида
, то имеем неопределенность вида  .
.
Для решения задачи используем правило 2.1 (см. таблицу). Разделим числитель и знаменатель на  . Мы имеем право это сделать, потому что значение
. Мы имеем право это сделать, потому что значение  не рассматривается, и, значит
не рассматривается, и, значит  .
.
 .
.
Ответ:  .
.
Пример 2.
Вычислить предел функции  .
.
Решение. Имеем неопределенность  . По правилу 2.1 разделим числитель и знаменатель на
. По правилу 2.1 разделим числитель и знаменатель на  .
.






0 0
Тогда
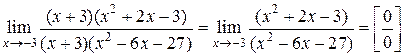 .
.
Еще раз разделим числитель и знаменатель на  :
:
 .
.
Ответ: 
Пример 3.
Вычислить предел функции  .
.
Решение. Имеем неопределенность  . По правилу 2.2 умножим числитель и знаменатель на выражение, сопряженное числителю и применим формулу
. По правилу 2.2 умножим числитель и знаменатель на выражение, сопряженное числителю и применим формулу  :
:

Ответ:  .
.
Пример 4.
Вычислить предел функции  .
.
Решение.
Т.к. здесь неопределенность  и знаменатель содержит иррациональность, то, используя правило 2.2, умножим числитель и знаменатель дроби на неполный квадрат (т.к. корень кубический) и применим формулу
и знаменатель содержит иррациональность, то, используя правило 2.2, умножим числитель и знаменатель дроби на неполный квадрат (т.к. корень кубический) и применим формулу  . Имеем
. Имеем





Ответ:  .
.
Пример 5.
Вычислить предел  .
.
Решение.
Т.к функция у= 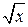 непрерывна при всех x,то, переходя к пределу под знаком непрерывной функции, получаем
непрерывна при всех x,то, переходя к пределу под знаком непрерывной функции, получаем
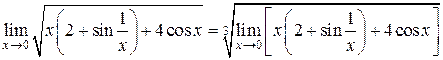 .
.
Т.к x – бесконечно малая функция в точке x =0,
а функция 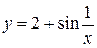 -ограниченная в окрестности точки x = 0,
-ограниченная в окрестности точки x = 0,
то  -бесконечно малая функция в точке x = 0 (произведение бесконечно малой функции на ограниченную функцию – есть бесконечно малая функция), т.е.
-бесконечно малая функция в точке x = 0 (произведение бесконечно малой функции на ограниченную функцию – есть бесконечно малая функция), т.е.  .
.
Т.к. функция  непрерывна в точке x = 0,
непрерывна в точке x = 0,
то  .
.
Используя основные теоремы о пределе функции в точке, получим
 .
.
Ответ:  .
.






