21) A  ; B
; B 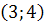 ; C
; C 
22) A  ; B
; B  ; C
; C 
23) A  ; B
; B  ; C
; C 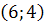
24) A  ; B
; B  ; C
; C 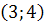
25) A  ; B
; B 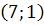 ; C
; C 
26) A  ; B
; B  ; C
; C 
27) A  ; B
; B  ; C
; C 
28) A  ; B
; B  ; C
; C 
29)А(-5,5); В(-5;7); С(5;0)
30)А(6;0); В(6;-3); С(8;2)
3. Найти пределы:
31. а)  b)
b) 
c) 
32. a)  b)
b) 
c) 
33. a)  b)
b) 
c) 
34. a)  b)
b) 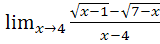
c) 
35. a)  b)
b) 
c) 
36. a)  b)
b) 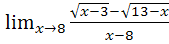
c) 
37. a)  b)
b) 
c) 
38. a)r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  b)
b) 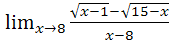
c) 
39. a)  b)
b) 
c) 
40. a)  b)
b) 
c) 
4.Вычислите определитель:
41)  42)
42)  43)
43) 
44)  45)
45)  46)
46) 
47)  48)
48)  49)
49) 
50)  .
.
Решите систему линейных уравнений методом Крамера и методом Гуасса.
51) s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:noProof/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:fareast="RU"/></w:rPr><m:t> </m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  52)
52) 
53)  54)
54) 
55)  56)
56) 
57)  58)
58) 
59)  60)
60) 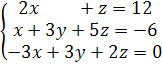
6.Найдите производные.
61) а)  b)
b) 
62) a)  b)
b) 
63) a)  b)
b) 
64) a)  b)
b) 
65) a)  b)
b) 
66) a) 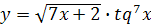 b)
b) 
67) a)  b)
b) 
68) a)  b)
b) 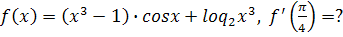
69) a)  b)
b) 
70) a) 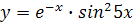 b)
b) 
Исследуйте функции и постройте их графики.
71) a)  b)
b) 
72) a) 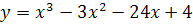 b)
b) 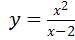
73) a)  b)
b) 
74) a) 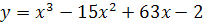 b)
b) 
75) a) 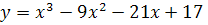 b)
b) 
76) a)  b)
b) 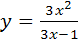
77) a)  b)
b) 
78) a) 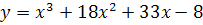 b)
b) 
79) a) 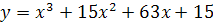 b)
b) 
80) a)  b)
b) 
8.Найдите интегралы:
81) а)  , b)
, b)  c)
c) 
82) a)  b)
b)  c)
c) 
83) a)  b)
b)  c)
c) 
84) a)  b)
b) 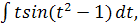 c)
c)  ;
;
85) a)  b)
b)  c)
c) 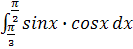 ;
;
86) a)  b)
b)  c)
c) 
87) a)  b)
b)  c)
c) 
88) a)  b)
b) 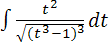 c)
c) 
89) a)  , b)
, b)  c)
c) 
90) a)  b)
b)  c)
c) 
9.Вычислить площадь фигуры, ограниченной линиями:
91) y=  и x-3y+6=0 92) y=
и x-3y+6=0 92) y=  и x=0, y=0
и x=0, y=0
93) y=2  , x=2, x=4 94)
, x=2, x=4 94)  =9x, x=1; x=9
=9x, x=1; x=9
95) y=  -x, x=0;x=2 96) y=2
-x, x=0;x=2 96) y=2  -x+2; x=3 и осями координат
-x+2; x=3 и осями координат
97) y =9-  и осью OX 98) y=
и осью OX 98) y=  -5x+4 и осью OX
-5x+4 и осью OX
99) y=2x-  и y=x 100) y=
и y=x 100) y=  и y=4-x
и y=4-x
10.Преобразовать в тригонометрическую и показательную форму комплексное число:
101)  +
+  106)
106) 
102)  107)
107) 
103)  108)
108) 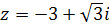
104)  +
+  109)
109) 
105)  +
+  110)
110) 
11.Разложите в ряд Маклорена функцию: 
111) f(x)=  116) f(x)=ln(1+2x)
116) f(x)=ln(1+2x)
112) f(x)=sin  117) f(x)=cos 3x
117) f(x)=cos 3x
113) f(x)=sin3x 118) f(x)= 
114) f(x)=cos  119) f(x)=sin 2x
119) f(x)=sin 2x
115) f(x)=ln(1-3x) 120) f(x)=cos 2x
А) Решите дифференциальное уравнение с начальными условиями.
Б) Найдите общее решение дифференциального уравнения.
121 а). 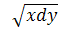 -
-  = 0, при x = 0, y = 0
= 0, при x = 0, y = 0
б) 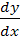 + y =
+ y = 
122. а) 
 = 0, при x=0, y = 3.
= 0, при x=0, y = 3.
б) y’ -  = -1
= -1
123. a)  = y, при х = 0, у =2,
= y, при х = 0, у =2,
б) у” = x +1, если при х=0, y=2, y’ = - 
124. a) y” – 2y’ +2у = 0.
б) ds = (3  -2t) dt, s = 4, при t = 2.
-2t) dt, s = 4, при t = 2.
125. a)  dx = 3
dx = 3 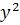 dy
dy
б) y’ + y tgx = 0, eсли у = 2 при х = 0.
126. а)  -
-  , y=4 при x=0
, y=4 при x=0
б) y” -9y = 0.
127. a) ydx + (1-y) xdy = 0.
б)  =
=  , y = 2 при х = 0.
, y = 2 при х = 0.
128. а) 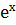 у” =
у” =  .
.
б)  dy -
dy - 
 dx = 0, y = 1 при х = -1.
dx = 0, y = 1 при х = -1.
129. а) y” + 4y’ + 3y = 0.
б) t wx:val="Cambria Math"/><w:i/><w:sz w:val="32"/><w:sz-cs w:val="32"/></w:rPr><m:t>x</m:t></m:r></m:e></m:rad><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="32"/><w:sz-cs w:val="32"/></w:rPr><m:t>dy</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  =
= 
130. a)  =
=  , y = 4 при х = -2. б) x ydx = (1 +
, y = 4 при х = -2. б) x ydx = (1 +  ) dy
) dy






