Определение: дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функцию у и ее производные или дифференциалы.
Решением (или интегралом) дифференциального уравнения, называется такая функция, которая обращает это уравнение в тождество.
Общим решением (или интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения.
Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных условиях.
Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.
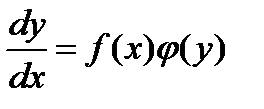 Дифференциальные уравнения первого порядка с разделяющимися переменным.
Дифференциальные уравнения первого порядка с разделяющимися переменным.
Уравнение вида называется дифференциальным уравнением с разделяющимися переменными.
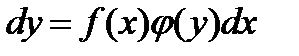 Для решения этого уравнения нужно сначала разделить переменные:
Для решения этого уравнения нужно сначала разделить переменные:
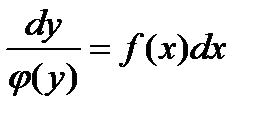
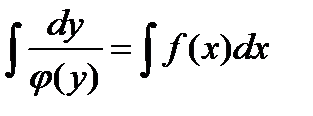
Затем интегрируем обе части данного равенства:
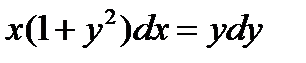 Пример.
Пример.
Найти общее решение уравнения:
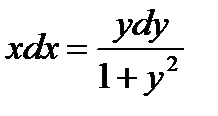 Разделим переменные:
Разделим переменные:
Проинтегрируем обе части равенства:
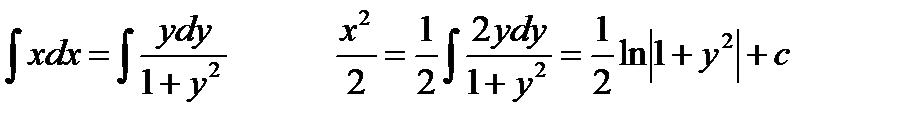
Или
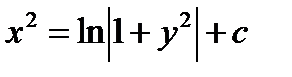 - общее решение дифференциального уравнения.
- общее решение дифференциального уравнения.
Линейные уравнения.
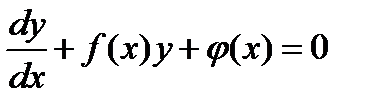
Линейные уравнения – это уравнения вида:
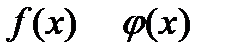
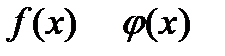 Где и - функции от
Где и - функции от 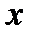 . В частном случае
. В частном случае
и могут быть постоянными величинами.
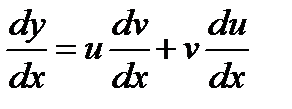
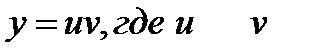 Это уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки и - новые функции от
Это уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки и - новые функции от 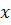 . Дифференциала этого равенства по
. Дифференциала этого равенства по 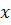
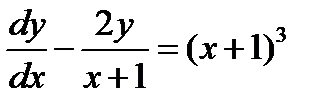 Пример.
Пример.
Найти общее решение уравнения
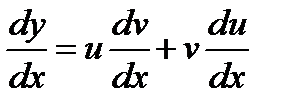 Выполним замену
Выполним замену 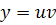 , и продифференцируем
, и продифференцируем
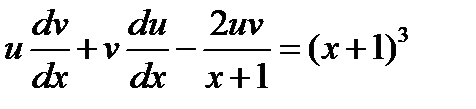 это равенство по
это равенство по 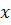 , подставив в
, подставив в
yравнение, получим
Т. к. одну из вспомогательных функций 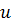 или
или 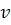
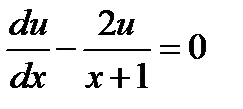 можно выбрать произвольно, то в качестве
можно выбрать произвольно, то в качестве 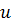 возьмем одно из частных решений уравнения
возьмем одно из частных решений уравнения
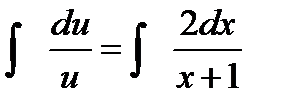
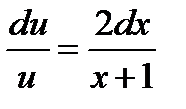 Разделив в этом уравнении переменные и интегрируя получим:
Разделив в этом уравнении переменные и интегрируя получим:
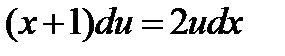 или
или 
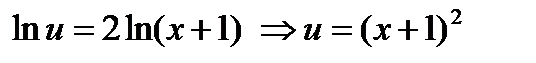
(произвольную постоянную С принимаем равной нулю, так как находим одно из частных решений).
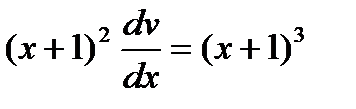
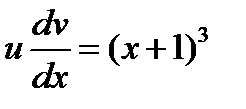 Подставив теперь выражение для
Подставив теперь выражение для 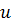 в уравнение
в уравнение
 получим
получим
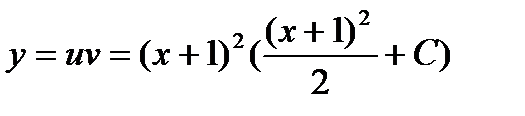 или разделяя переменные и
или разделяя переменные и
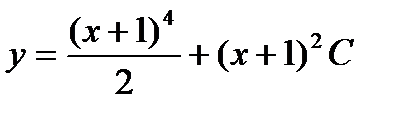 интегрируя, будем иметь
интегрируя, будем иметь
Зная 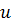 и
и 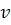 , найдем
, найдем
Ряды.
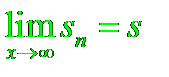 Бесконечная последовательность чисел, соединенных знаком сложения,
Бесконечная последовательность чисел, соединенных знаком сложения, 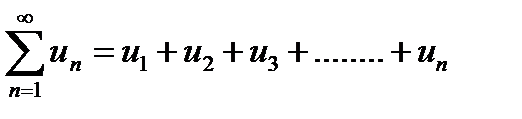 называется числовым рядом.
называется числовым рядом.
Если этот предел существует и конечен, то ряд называют сходящимся.
Если же этот предел бесконечен или вовсе не существует, то ряд называют расходящимся.
Условие 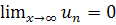 называется необходимым условием сходимости ряда.
называется необходимым условием сходимости ряда.
Признаки сходимости рядов:
1.Признак сравнения.
Пусть даны два ряда с положительными членами
u 1+ u 2+ u 3+…+ u n+…
v 1+ v 2+ v 3+…+ v n+…
И пусть для всех значений k = 1, 2 … выполняются неравенства 
Тогда:
А) если 1 ряд сходится, то и сходится 2 ряд;
Б) если 2 ряд расходится, то и расходится 1 ряд
2. Признаки Даламбера и Коши
Признак Даламбера:
Пусть дан ряд с положительными членами
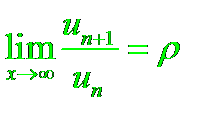 u 1+ u 2+ u 3+…+ u n+…
u 1+ u 2+ u 3+…+ u n+…
И пусть существует конечный предел
Тогда:
а) если 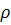 <1, то ряд сходится;
<1, то ряд сходится;
б) если 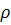 >1,то ряд расходится;
>1,то ряд расходится;
г) если 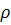 =1, то вопрос о сходимости ряда остается открытым;
=1, то вопрос о сходимости ряда остается открытым;
Признак Коши:
Пусть дан ряд с положительными членами
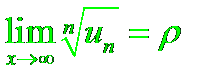 u 1+ u 2+ u 3+…+ u n+…
u 1+ u 2+ u 3+…+ u n+…
И пусть существует конечный предел
Тогда:
а) если 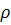 <1, то ряд сходится;
<1, то ряд сходится;
б) если 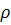 >1,то ряд расходится;
>1,то ряд расходится;
г) если 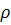 =1, то вопрос о сходимости ряда остается открытым;
=1, то вопрос о сходимости ряда остается открытым;
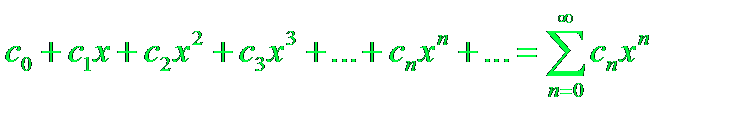 Степенные ряды.
Степенные ряды.
Степенным рядом называют ряд вида:
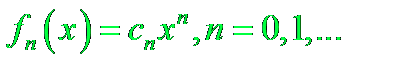 Эти ряды являются частным случаем функциональных рядов. Общий член ряда имеет вид:
Эти ряды являются частным случаем функциональных рядов. Общий член ряда имеет вид:
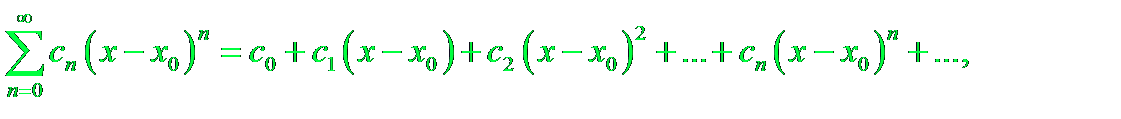 Числа cn называют коэффицентами степенного ряда. Рассматривают также ряды
Числа cn называют коэффицентами степенного ряда. Рассматривают также ряды
Называемые степенными рядами в точке х0.
Ряд вида
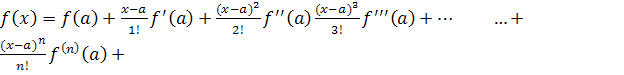 …
…
Называется рядом Тейлора.
Если в ряде Тейлора положим  , то получим частный случай ряда Тейлора, который называется рядом Маклорена.
, то получим частный случай ряда Тейлора, который называется рядом Маклорена.
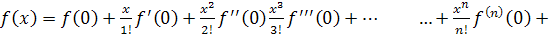 … (1)
… (1)
Пример:
Разложить функцию в ряд Маклорена.
t wx:val="Cambria Math"/><w:i/><w:noProof/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US" w:fareast="RU"/></w:rPr><m:t>x</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 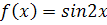
Решение. Найдем производные и значения функции и производных в точке х=0:

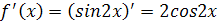
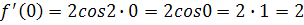
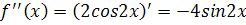
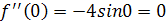
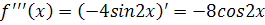
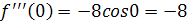
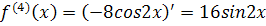
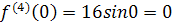 подставим полученные значения в формулу (1), получим:
подставим полученные значения в формулу (1), получим:
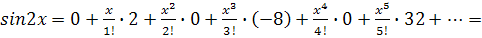
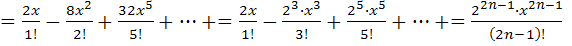
Контрольные задания.
1.
11. Вычислить угол между векторами s w:val="28"/></w:rPr><m:t>a</m:t></m:r></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  и
и 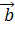 , если
, если 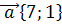 и
и 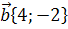
12. Вычислить длину вектора 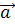 -
-  , если
, если 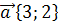 и
и 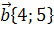
13. Вычислить длину вектора 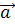 +
+  , если
, если 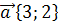 ,
, 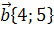
14. Вычислите проекцию вектора 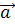 на ось
на ось 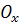 , если угол между осью
, если угол между осью 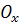 и направлением вектора равен
и направлением вектора равен  , а |
, а | 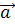 |=12
|=12
15. Даны векторы 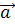 и
и  , угол между ними
, угол между ними  . Построить вектор 2
. Построить вектор 2 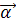 -
-  и определить его длину, если |
и определить его длину, если | 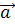 |=2; |
|=2; |  |=3
|=3
16. Даны векторы 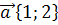 и
и 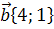 . Найти длину вектора 3
. Найти длину вектора 3 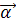 -2
-2  .
.
17. Дано векторы | 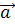 |=5; |
|=5; | 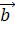 |=4 и
|=4 и 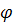 =(
=(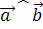 ) =
) = 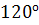 .
.
Найти: а) 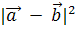 ; б)
; б) 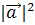 .
.
18. Построить вектор 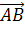 , если A
, если A 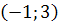 ; B
; B 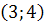 и найти его длину.
и найти его длину.
19. Найти скалярное произведение векторов 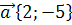 и
и 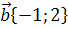 и угол между ними.
и угол между ними.
20. Найти модуль вектора 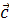 = 2
= 2 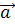 -3
-3  , если |
, если | 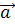 |=2; |
|=2; | 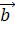 |=1 и (
|=1 и (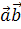 )=
)=