Упражняясь по нахождению той или иной величины из формулы, ты выполнял завершающую математическую часть каких-то физических задач. Если упражнение – повторное выполнение действий, то задача – это вопрос или проблема, требующие решения на основании знаний и размышления.
Простейшие задачи сводятся к подстановке чисел в основную формулу, которая определяет физическую величину, соотношение между величинами или закон.
Так, для нахождения плотности, зная массу и объём тела, достаточно подставить их числовые значения в формулу, дающую определение плотности. В «Дано» я не буду указывать числовые значения величин, считая, что они известны.
1.Дано:

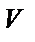
| 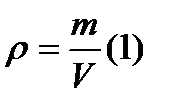
|

|
Такие задачи – мечта учащегося! Многие считают, что решение любой задачи сводится к нахождению необходимой формулы. Но это не так. Та же самая формула позволяет решить ещё две задачи – найти массу m и объём тела V.
2.Дано
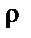

|  Следовательно Следовательно  т.е.
т.е.  и и

|

|
В случае 2, из исходной формулы выражается m по алгоритму для группы B. Если ты выработал автоматизм при работе с формулами, то сразу сможешь записать формулу (2) – решение этой задачи. Но это не значит, что первая и вторая формулы равноценны. Формула (1) – исходная, основная, а (2) – производная, результат математических преобразований формулы (1).
3.Дано:
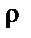
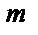
|  Следовательно Следовательно 
 а а  и и 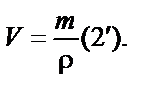
|

|
В случае 3, пользуясь тем же алгоритмом, находим V. И снова получаем производную от (1) формулу. И точно так же, решая и эту задачу, мы можем опустить математические преобразования и сразу записать формулу для нахождения V. Но различия между формулой (1) и производными из неё формулами существенны: в большинстве случаев основная формула ниоткуда математически не выводится, соотношения между величинами этой формулы «подсмотрены» в природе.
Итак, простейшие физические задачи сводятся к подстановке чисел в готовую формулу, или формулу, полученную из готовой за счёт математических преобразований. Следующие по сложности задачи те, в которых одна из величин, представленных в формуле, не дана непосредственно, и её надо предварительно найти. Например:
4.Дано:



|  Но
Но  Следовательно,
Следовательно,

|

|
В данном случае  нельзя найти из формулы (1) сразу, поскольку неизвестно
нельзя найти из формулы (1) сразу, поскольку неизвестно  . Из условий задачи – и здесь начинают требоваться знания и размышления! – следует формула (2), которая позволяет это сделать. Подставив вместо значений
. Из условий задачи – и здесь начинают требоваться знания и размышления! – следует формула (2), которая позволяет это сделать. Подставив вместо значений  и
и  числа, найдём числовое значение
числа, найдём числовое значение  , а затем из (1) и
, а затем из (1) и  .
.
Формулу (А4) – называют решением задачи в общем виде. Решение задачи в общем виде позволяет производить вычисления один раз, но оно важно не только этим. В старших классах почти все задачи стараются решать в общем виде, и в дальнейшем ты поймёшь почему.
Пока же рассмотрим, за счёт чего задачи усложняются. Более сложной задачей является следующая:
5.Дано:



| Известно, что:
 , ,  ,а ,а  Следовательно,
Следовательно, 
|

|
Видно, что эта задача отличается от предыдущей тем, что из формулы (1) невозможно сразу найти  потому, что не известна не только величина
потому, что не известна не только величина  , но и величина
, но и величина  .
.
Формула (3) позволяет найти числовое значение  , подставив числовые значения
, подставив числовые значения  и
и  , затем найти по формуле (2) числовое значение
, затем найти по формуле (2) числовое значение 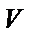 , и только затем решить задачу, используя формулу (1). Здесь, опять же указано и решение в общем виде (А5).
, и только затем решить задачу, используя формулу (1). Здесь, опять же указано и решение в общем виде (А5).
Ты видишь, что усложнение решения только количественное – вместо одного предварительного вычисления величины, нужно делать два. Выстраивается своеобразная «цепочка» формул. Но таких предварительных вычислений может быть и больше, поэтому, чтобы не запутаться, чтобы «цепочка» не перехлестнулась, необходимо нумеровать все формулы.
Эта задача интересна тем, что в формуле (3) присутствует постоянная величина – так называемая константа –  Если бы ты не знал, что
Если бы ты не знал, что  - известная величина, то никогда бы не смог решить данной задачи. В физике есть свои постоянные величины – константы, кроме того, многие величины определены в опытах и сведены в таблицы справочников. Поэтому во многих случаях, недостающие для решения задачи величины, находятся в справочниках.
- известная величина, то никогда бы не смог решить данной задачи. В физике есть свои постоянные величины – константы, кроме того, многие величины определены в опытах и сведены в таблицы справочников. Поэтому во многих случаях, недостающие для решения задачи величины, находятся в справочниках.
Во всех рассмотренных случаях с точки зрения математики задача сводится к решениюуравнения с одним неизвестным.
В седьмом и восьмом классах почти все задачи представляют собой такие цепочки – короткие и длиннее – формул. Затем появляются задачи следующего уровня сложности – те, в которых искомую величину нельзя найти через другую формулу, поскольку искомая величина входит и в эту формулу. Например:
6.Дано:


| Известно, что:
 
|


|
Здесь для нахождения  необходимо найти
необходимо найти  , но в формуле (2) искомое
, но в формуле (2) искомое  присутствует в виде сомножителя. Таким образом, мы не можем найти числовое значение
присутствует в виде сомножителя. Таким образом, мы не можем найти числовое значение  , как в предыдущих задачах. С точки зрения математики в данной задаче наши формулы превращаются в систему двух уравнений с двумя неизвестными
, как в предыдущих задачах. С точки зрения математики в данной задаче наши формулы превращаются в систему двух уравнений с двумя неизвестными  и
и  . Такие системы уравнений в математике решаются разными способами, но чаще всего способом подстановки, когда из какого-либо уравнения выражают одно неизвестное, а затем подставляют найденное значение этого неизвестного в другое уравнение. Например:
. Такие системы уравнений в математике решаются разными способами, но чаще всего способом подстановки, когда из какого-либо уравнения выражают одно неизвестное, а затем подставляют найденное значение этого неизвестного в другое уравнение. Например:
 Если из первого уравнения мы найдём у, перенеся
Если из первого уравнения мы найдём у, перенеся  в правую часть, то получим:
в правую часть, то получим:
 Подстановка значения у в формулу (2) даёт новую систему равносильных уравнений:
Подстановка значения у в формулу (2) даёт новую систему равносильных уравнений:
 Теперь в уравнении
Теперь в уравнении 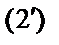 только одно неизвестное х, которое мы можем найти:
только одно неизвестное х, которое мы можем найти:
 Здесь раскрыли скобки у многочлена
Здесь раскрыли скобки у многочлена  . Далее сгруппируем и оставим в левой части второго уравнения слагаемые с х:
. Далее сгруппируем и оставим в левой части второго уравнения слагаемые с х:
 Вынесем х в левой части второго уравнения за скобки:
Вынесем х в левой части второго уравнения за скобки:
 Или
Или
 Отсюда, поделив левую и правую части второго уравнения на (-3), получим:
Отсюда, поделив левую и правую части второго уравнения на (-3), получим:
 То есть
То есть
 Мы нашли, чему равняется х, и, подставив его значение в первую формулу, найдём у.
Мы нашли, чему равняется х, и, подставив его значение в первую формулу, найдём у.
 То есть
То есть

Конечно, никто так подробно систему уравнений не решает, а опускает последовательность действий, подразумевая их. Получается примерно так:
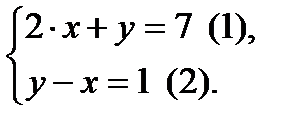
Из (1) следует: 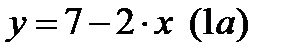 . Подставляя значение у из
. Подставляя значение у из 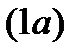 в (2) получаем:
в (2) получаем:  или
или  , откуда
, откуда  .
.
Подставляя значения х в формулу 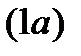 , получаем
, получаем  или
или  .
.
Поскольку, опуская последовательность действий, возрастает вероятность ошибок, важно всегда писать, какие преобразования, с какой величиной и формулой ведутся.
Если ещё раз посмотреть на систему уравнений

вспомнить, что решение мы начали с того, что выразили из первого уравнения величину у, то становится ясно – это один из возможных путей решения данной системы уравнений. Можно было начать, выразив:
1. х из первого уравнения,
2. у из первого уравнения (что и было сделано),
3. у из второго уравнения,
4. х из второго уравнения.
Выбор конкретного пути нахождения неизвестных величин остаётся за решающим систему уравнений. В нашем случае мы начали с выражения у из первого уравнения достаточно произвольно, просто потому, что в первом уравнении удобнее выражать величину, числовой коэффициент которой равен 1. Кстати, нужно помнить, что коэффициенты (+1) и (-1) почти всегда в уравнениях и формулах не пишутся. То есть, система уравнений, которая только что рассматривалась, в развёрнутом виде записывается так:

Если все преобразования, которые мы производили, решая систему уравнений, ясны, то вернёмся к задаче 6.
Дано:


| Известно, что:
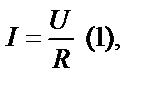

|


|
Разве формулы (1) и (2) похожи на уравнения, в которых мы искали х и у? Но если освободиться от знаменателя в формуле (1) и условиться, что  , а
, а 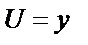 , то получим систему уравнений:
, то получим систему уравнений:
 Или
Или 
Эта система уравнений отличается от той, которую рассматривали, только тем, что вместо числовых коэффициентов здесь записаны буквенные коэффициенты. Сложность решения физических задач и в том, что в формулах, которые образуют систему уравнений, нет привычных записей неизвестных через  , а коэффициенты чаще всего представлены буквами, а не числами.
, а коэффициенты чаще всего представлены буквами, а не числами.
Решим нашу задачу.
Дано:


| Известно, что:


|


|
Поскольку в данной задаче  уже выражено в уравнении (1), подставим её значение в формулу (2). Получим:
уже выражено в уравнении (1), подставим её значение в формулу (2). Получим:
 или
или  . Освободившись от знаменателя, умножив на него обе части, имеем:
. Освободившись от знаменателя, умножив на него обе части, имеем:
 . Поменяв части местами, и извлекая из них квадратный корень, поскольку найдена не искомая величина, а её квадрат, получим:
. Поменяв части местами, и извлекая из них квадратный корень, поскольку найдена не искомая величина, а её квадрат, получим:

Подставляя значение  из формулы (А6-1) в формулу (1), найдём
из формулы (А6-1) в формулу (1), найдём  .
.

И снова следует заметить, что это один из вариантов решения.
Рассмотрим следующую задачу.
7.Дано:



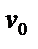
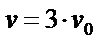
| Известно, что:

|

|
Взяв (1) и (2) как систему из двух уравнений, видим, что неизвестных величин тоже две –  и
и 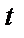 , хотя в задаче требуется найти только одну из них. При решении физических задач иногда одну из неизвестных величин в виде числа находить не нужно. Видно, что найти
, хотя в задаче требуется найти только одну из них. При решении физических задач иногда одну из неизвестных величин в виде числа находить не нужно. Видно, что найти  мы снова можем тремя способами, поскольку в (2) неизвестная величина
мы снова можем тремя способами, поскольку в (2) неизвестная величина  уже выражена.
уже выражена.
Выразим  из (1).
из (1).  , откуда
, откуда  Подставив значение
Подставив значение  в (2), имеем:
в (2), имеем:  В знаменателе у нас получилась «двухэтажность» из-за деления на дробь
В знаменателе у нас получилась «двухэтажность» из-за деления на дробь  . Но деление на дробь можно заменить умножением на дробь обратной данной, в данном случае на
. Но деление на дробь можно заменить умножением на дробь обратной данной, в данном случае на  .Следовательно,
.Следовательно, 
Освобождаясь от знаменателя в правой части, получаем:
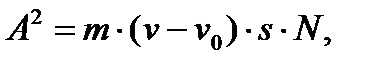 или
или 
Подставив значение  из (3) в формулу
из (3) в формулу 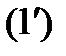 находим, что
находим, что

Поскольку по условиям задачи 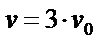 , получаем ответ:
, получаем ответ:
 или
или

Решение систем уравнений преподносит и неожиданности. К примеру:
8.Дано:



| Известно, что:


|

|
Проанализировав формулы, приходим к выводу, что неизвестных величин три -  Перед нами система из двух уравнений с тремя неизвестными. В математики доказано: сколько неизвестных, столько и уравнений должно быть, чтобы найти эти неизвестные. Однако, выразив, к примеру,
Перед нами система из двух уравнений с тремя неизвестными. В математики доказано: сколько неизвестных, столько и уравнений должно быть, чтобы найти эти неизвестные. Однако, выразив, к примеру,  из (2)
из (2) 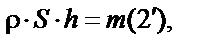 или после смены местами левой и правой частей
или после смены местами левой и правой частей  и подставив значение
и подставив значение 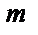 в (1), получим:
в (1), получим:
 . Поскольку величина
. Поскольку величина  сокращается, имеем:
сокращается, имеем: 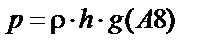 .
.
Таким образом, решение в общем виде может привести к сокращению неизвестных величин, которые не даны в условии задачи.
Но нет ли здесь противоречий с математикой? Никаких противоречий нет. Если посмотреть на уравнения
 и
и 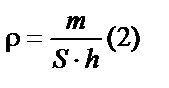 , то можно увидеть, что в правых частях присутствует дробь
, то можно увидеть, что в правых частях присутствует дробь  . То есть
. То есть  и
и  . Неизвестной величиной выступает именно эта дробь. Обозначив
. Неизвестной величиной выступает именно эта дробь. Обозначив  , получаем
, получаем
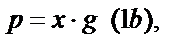 и
и
 , то есть систему двух уравнений с двумя неизвестными
, то есть систему двух уравнений с двумя неизвестными  и
и  .
.
Решение  - это вывод формулы
- это вывод формулы  . Но в отличие от нашей задачи, когда использовались две производные формулы, в курсе физики седьмого класса она выводится из 4-х основных формул.
. Но в отличие от нашей задачи, когда использовались две производные формулы, в курсе физики седьмого класса она выводится из 4-х основных формул.


 и
и  .
.
При известных величинах  неизвестными здесь оказываются величины
неизвестными здесь оказываются величины 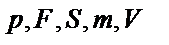 (пять, но теперь мы знаем, что их четыре из-за «хитрой» дроби
(пять, но теперь мы знаем, что их четыре из-за «хитрой» дроби  ). Если рассматривать четыре формулы как систему уравнений относительно этих неизвестных величин, то можно начинать решение с выражения любой неизвестной величины из любого уравнения. То есть, решение задачи 8 у нас началось с производной формулы
). Если рассматривать четыре формулы как систему уравнений относительно этих неизвестных величин, то можно начинать решение с выражения любой неизвестной величины из любого уравнения. То есть, решение задачи 8 у нас началось с производной формулы  которая получается в результате подстановки значения
которая получается в результате подстановки значения  из
из  в
в  , но могло начаться и с выражения
, но могло начаться и с выражения  из
из  или другим способом. Однако лучше подставить значение
или другим способом. Однако лучше подставить значение  из
из  в
в  , а значение
, а значение 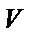 из
из 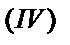 в
в  , потому что в результате сразу значительно уменьшается число уравнений (и неизвестных величин). Поскольку во многих задачах число исходных формул, то есть с точки зрения математики, число уравнений больше двух, то нужно в первую очередь поискать преобразования, которые ведут к такому уменьшению количества формул (уравнений).
, потому что в результате сразу значительно уменьшается число уравнений (и неизвестных величин). Поскольку во многих задачах число исходных формул, то есть с точки зрения математики, число уравнений больше двух, то нужно в первую очередь поискать преобразования, которые ведут к такому уменьшению количества формул (уравнений).
Иногда это достигается достаточно просто. Рассмотрим задачу.
9.Дано:



| Известно что:

|

|
Следует обратить внимание, что формулы, которые мы видим, в таблице формул нет. Данные формулы – результат записи условий конкретной задачи с их – формул – помощью. Как это делается, изучается на уроках физики. Мы же рассматриваем только математическую сторону решения физических задач.
Итак, неизвестными величинами в этой системе из четырёх уравнений являются искомая  , а также
, а также 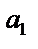 ,
,  ,
,  ,
,  , то есть пять величин. Снова остаётся надеяться, что две величины входят в состав дроби, которая сократится. Если бы это было не так, то для решения задачи пришлось искать пятое уравнение.
, то есть пять величин. Снова остаётся надеяться, что две величины входят в состав дроби, которая сократится. Если бы это было не так, то для решения задачи пришлось искать пятое уравнение.
Сразу видно, что для уменьшения числа уравнений нужно приравнять правые части (1)-(2) и (3)-(4), поскольку левые их части равны. Получаем два равносильных двум первоначальным парам уравнений.

В результате мы освободились от двух неизвестных 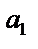 и
и  , осталось три неизвестных
, осталось три неизвестных  ,
,  и
и  , которые мы можем искать с помощью способа подстановки. Но уравнения (5) и (6) однородны: в левой части уравнений присутствует дробь
, которые мы можем искать с помощью способа подстановки. Но уравнения (5) и (6) однородны: в левой части уравнений присутствует дробь  , а в правой
, а в правой  . Если мы поделим друг на друга левые и правые части уравнений, то получим равносильное уравнение, а указанные дроби сократятся. Действительно:
. Если мы поделим друг на друга левые и правые части уравнений, то получим равносильное уравнение, а указанные дроби сократятся. Действительно:
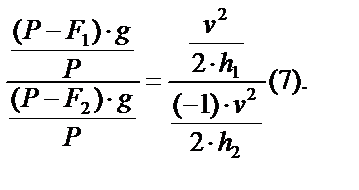 Или, поскольку поделить на дробь – это умножить на дробь обратную данной,
Или, поскольку поделить на дробь – это умножить на дробь обратную данной, 
После сокращения имеем:  В уравнении (8) осталась только одна неизвестная искомая величина, которая легко находится, если использовать основное свойство пропорции.
В уравнении (8) осталась только одна неизвестная искомая величина, которая легко находится, если использовать основное свойство пропорции.
 Искомая величина входит в состав многочлена, и после нахождения этого многочлена
Искомая величина входит в состав многочлена, и после нахождения этого многочлена  легко выражается
легко выражается 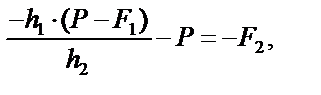 или
или 
Вообще же, если есть два уравнения, то равносильное им уравнение можно получить не только делением частей уравнений друг на друга, но и умножением, и сложением (вычитанием). Действительно, если  то и
то и  ,
,  ,
, 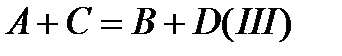 и
и 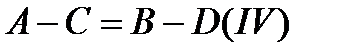 .
.
Уже ясно, что не существует раз и навсегда данных алгоритмов, которые позволяли бы единственным способом вести математические преобразования при решении задач. Почти каждая из задач требует размышлений не только со стороны физики – во время представления условий задачи в виде формул, но и со стороны математики – во время поиска оптимального, наиболее простого пути нахождения неизвестных величин из полученных формул. Рассмотрим ещё одну задачу. В ней уже специально не прописаны знаки умножения, как это всегда и делается при решении задач.
10.Дано:

| Известно, что:

|

|
Можно считать, что у нас имеются шесть уравнений. Неизвестными величинами выступают: искомая  , а также
, а также  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . Даже если знать, что величина
. Даже если знать, что величина  - это физическая константа, значение которой находится в справочнике, всё равно остаётся 8 неизвестных величин. Конечно, можно начать решение способом подстановки, в надежде, что две неизвестные величины входят в состав дробей и сократятся, но лучше внимательнее присмотреться к уравнениям. Из (6) мы сразу можем найти
- это физическая константа, значение которой находится в справочнике, всё равно остаётся 8 неизвестных величин. Конечно, можно начать решение способом подстановки, в надежде, что две неизвестные величины входят в состав дробей и сократятся, но лучше внимательнее присмотреться к уравнениям. Из (6) мы сразу можем найти  .
.
Если в (5) вынести в левой части за скобки  , а затем поделить на
, а затем поделить на  обе части, то получим:
обе части, то получим:
 поскольку
поскольку  Из
Из  мы можем найти
мы можем найти  , поскольку все величины, – в том числе и
, поскольку все величины, – в том числе и  , – известны.
, – известны.

Таким образом, у нас осталось четыре уравнения:
 Неизвестных в этих уравнениях пять -
Неизвестных в этих уравнениях пять -  ,
,  ,
,  ,
,  ,
,  .
.
Поскольку в (4) есть отношение величин  , которое мы можем получить, поделив левые части (1) и (2) друг на друга, сделаем это.
, которое мы можем получить, поделив левые части (1) и (2) друг на друга, сделаем это.
 Освободившись от «двухэтажности», умножив на дробь, обратную дроби в знаменателе правой части, получим:
Освободившись от «двухэтажности», умножив на дробь, обратную дроби в знаменателе правой части, получим:

Или после сокращений в правой части: 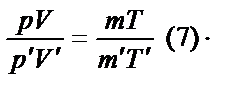
Таким образом, из уравнений (1) и (2) мы получили равносильное им уравнение (7). Из него, умножив левую и правую части на 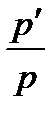 , чтобы сократить
, чтобы сократить 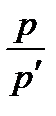 получаем:
получаем:  Теперь мы можем приравнять правые части (4) и
Теперь мы можем приравнять правые части (4) и 
 Это равносильное уравнение уравнениям (4) и
Это равносильное уравнение уравнениям (4) и  Теперь мы свели систему уравнений к двум уравнениям – (3) и (8). Подставив значение
Теперь мы свели систему уравнений к двум уравнениям – (3) и (8). Подставив значение  из (3) в (8) получим:
из (3) в (8) получим:

Это уравнение равносильно всем шести уравнениям. В нём одна неизвестная искомая величина  , которую нетрудно найти. Учитывая, что (9) – пропорция, воспользуемся основным её свойством. Тогда
, которую нетрудно найти. Учитывая, что (9) – пропорция, воспользуемся основным её свойством. Тогда

Умножив в левой части одночлен  на многочлен
на многочлен  , получаем:
, получаем:

Перенеся сомножители с  в левую часть, а одночлен без неизвестной величины в правую, имеем:
в левую часть, а одночлен без неизвестной величины в правую, имеем:
 Вынеся в левой части
Вынеся в левой части  за скобки, приходим к уравнению
за скобки, приходим к уравнению  Отсюда, поделив на сомножитель при
Отсюда, поделив на сомножитель при  обе части, решаем нашу задачу:
обе части, решаем нашу задачу:

Эта задача, кроме всего прочего, показывает, насколько важно быть внимательным, ведя преобразования. Достаточно в одном месте перепутать величины  и
и  ,
,  и
и  ,
,  и
и  ,
,  и
и  или
или  и
и  , как задача никогда не будет решена.
, как задача никогда не будет решена.






