Действительно, если мы умножим обе части пропорции последовательно на знаменатели, или сразу на произведение знаменателей, то после сокращений получим равенство произведений крайних и средних членов.
 ,
, 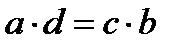
Основное свойство пропорции упрощает преобразования, поскольку любое равенство можно представить в виде пропорции, представив одночлены или многочлены в виде дроби со знаменателем 1.
Например:
 можно представить в виде
можно представить в виде  и сразу освободиться от знаменателя
и сразу освободиться от знаменателя  , поскольку
, поскольку  .
.
| Алгоритм преобразований | Исходная и преобразованные формулы. | Пример поиска искомой величины в физической формуле. |
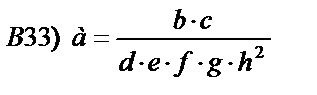
| 
| |
| 1.При наличии знаменателя, освободиться от него, умножив на знаменатель правую и левую части равенства (в случае пропорции – перемножить крайние и средние члены). | 

|


|
| 2.Если искомая величина (её квадратный корень или квадрат) не найдена, а находится в составе одночлена, найти её, поделив обе части равенства на сомножитель(и) искомой величины. |  Сомножителями
Сомножителями  являются
являются



|  Сомножителем
Сомножителем  в одночлене в одночлене 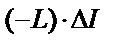 является
является 

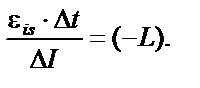
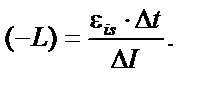
|
| 3.Если в результате преобразований найдено отрицательное значение искомой величины (её квадратного корня или квадрата), умножить на (-1) обе части равенства (поменять знаки левой и правой частей равенства на противоположные). |

| |
| 4.Если найден квадратный корень искомой величины, возвести левую и правую части равенства в квадрат. | ||
| 5.Если найден квадрат искомой величины, извлечь квадратный корень из левой и правой части равенства |  
|
Группа C. В правой части формул группы C присутствуют многочлены, квадратные корни и квадраты многочленов.
| Алгоритм преобразований | Исходная и преобразованные формулы | Пример поиска искомой величины в физической формуле. |

| 

| |
| 1.При наличии знаменателя, освободиться от него, умножив на знаменатель правую и левую части равенства (в случае пропорции – перемножить крайние и средние члены). | 

| 
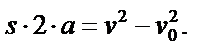
|
| 2.Если искомая величина (её квадратный корень или квадрат) не найдена, а входит в состав одночлена или является сомножителем многочлена, найти её, поделив обе части равенства на сомножитель(и) искомой величины. | 

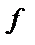 – входит в состав одночлена – входит в состав одночлена 


| |
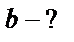

 – сомножитель многочлена – сомножитель многочлена 

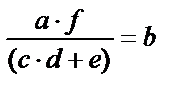 Или
Или

| ||
| 3.Если искомая величина (её квадратный корень или квадрат) находится в составе многочлена, найтимногочлен, поделив левую и правую части равенства на сомножитель(и) многочлена. | 
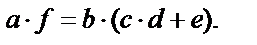
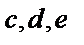 – входят в состав многочлена – входят в состав многочлена 
 Или
Или
 И
И
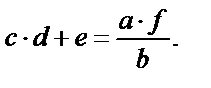
| |
| 4.Если многочлен является квадратным корнем, возвести левую и правую части равенства в квадрат. | ||
| 5.Если многочлен является квадратом, извлечь из левой и правой части равенства квадратный корень. | ||
| 6.Если искомая величина (её квадратный корень или квадрат) в составе многочлена не имеет сомножителей, найти её, перенеся второе СЛАГАЕМОЕ в другую часть, поменяв его знак на противоположный | 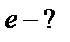 Поскольку в
Поскольку в

 – слагаемое, которое не имеет сомножителей, то – слагаемое, которое не имеет сомножителей, то

| Поскольку
 , то , то
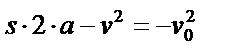 , и , и

|
| 7.Если искомая величина (её квадратный корень или квадрат) в составе многочлена является сомножителем одночлена, найти этот одночлен, перенеся другое СЛАГАЕМОЕ в другую часть, поменяв его знак на противоположный. | 

 – сомножители одночлена в составе многочлена – сомножители одночлена в составе многочлена 

| |
| 8.Найти искомую величину (её квадратный корень или квадрат), поделив правую и левую части равенства на сомножитель(и) при искомой величине. |  Если
Если  то то
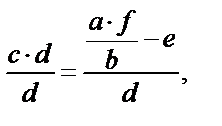 и и
 Аналогично находится
Аналогично находится 
| |
| 9.Если в результате преобразований найдено отрицательное значение искомой величины (её квадратного корня или квадрата), умножить на (-1) обе части равенства. | У нас
 Следовательно,
Следовательно,
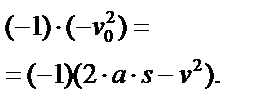 И
И
 Или
Или
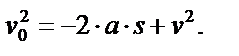
| |
| 10.Если найден квадратный корень искомой величины, возвести левую и правую части равенства в квадрат. | ||
| 11.Если найден квадрат искомой величины, извлечь квадратный корень из левой и правой части равенства | Из
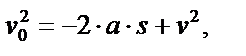 находим находим
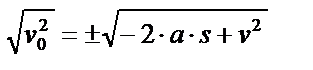 и и
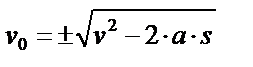
|
Группа D. В группе D в правой части формул присутствует сумма дробей или сумма одночлена и дроби.
Из курса математики нужно вспомнить сложение дробей с одинаковыми знаменателями, приведение дробей к общему знаменателю, а также вынесение общего множителя за скобки.
Правило сложения дробей с одинаковыми знаменателями:
чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.






