Алгоритмы работы с формулами.

ПОСОБИЕ ПО РАБОТЕ С ФИЗИЧЕСКИМИ ФОРМУЛАМИ

Для учащихся 7-11-х классов.

 

 

ПЕНЗА – 2011 год.

 

 

Условные обозначения:

 

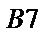– номер 7-ой группы аналогичных формул.

 

23 – номер формулы.

– нахождение какой величины ведётся

из формулы.

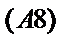– решение 8-ой задачи в общем виде.

 

 

ОГЛАВЛЕНИЕ.

ВВЕДЕНИЕ… …………………………………………………………………………….…4

РАЗДЕЛ I. Состав физических формул и нахождение величин из формул ………...5

1. Алфавиты… ……………………………………………………………………………....5

2.Таблица физических формул и их математического представления… …………..6

3. Алгоритмы работы с формулами… ……………………………………………….…..15

Группа А… ………………………………………………………………………………..15

Группа B …………………………………………………………………………………..16

Группа C …………………………………………………………………………………..17

Группа D …………………………………………………………………………………..20

Группа E …………………………………………………………………………………...22

РАЗДЕЛ II. Работа с формулами при решении задач по физике… ………………....23

РАЗДЕЛ III. Контрольные задачи… ……………………………………………………..32

 

ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА ……………………………………………………....34

 

ПРИЛОЖЕНИЕ. ПОРЯДОК ОФОРМЛЕНИЯ РЕШЕНИЙ ЗАДАЧ ПО ФИЗИКЕ… ……..35

ВВЕДЕНИЕ.

Уважаемый учащийся! Данное пособие позволит тебе выработать умения и навыки работы с физическими формулами. Ты будешь чувствовать себя уверенно не только на уроках физики, но выработанные умения и навыки пригодятся тебе в дальнейшем, потому что формулы сопутствуют большинству видов человеческой деятельности.

Физика пронизана формулами. С их помощью выражаются законы природы и соотношения между величинами. Формулой называют запись какого-нибудь правила с помощью букв. Если в математике в большинстве случаев используют буквы латинского алфавита, то в физике широко используются буквы греческого алфавита, который в школе не изучается. Кроме того, для обозначения физических величин к буквам приписывают справа различные знаки, которые называются нижними и верхними индексами, а также надчёркивают. В качестве знаков используют цифры, буквы, – и русского алфавита тоже, – штрихи, а также их комбинации; надчёркивают стрелочкой и линией.

Например: 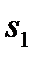, , , , 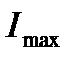, , 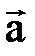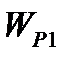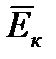и т.д..

Буква с индексами и надчёркиваниями в формуле составляет единое целое. Формулы бывают простыми и достаточно сложными. Формулы – это равенства. Например: 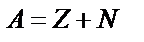и .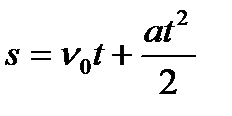

При изучении физики, решении задач постоянно приходится выражать из формул ту или иную величину, то есть, вести математические преобразования. Для этого надо знать, какими операциями – сложения, вычитания, умножения, деления, возведения в степень и т.д. – соединены в формуле физические величины, представленные буквами. Для облегчения задачи нахождения той или иной величины, любую физическую формулу можно представить в виде математической формулы, с прописанными знаками умножения, которые при записи обычно опускаются, и восстановить скобки.

Например, формулы 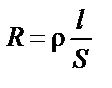и 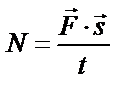можно представить в виде .

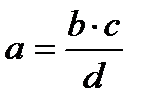Такая замена физических формул позволяет видеть, какие математические преобразования надо вести, чтобы найти какую-либо физическую величину.

Данное пособие предназначено для постоянной работы по овладению навыками работы с формулами. Только небольшая часть учащихся обладает природными математическими задатками, которые позволяют им с минимальными усилиями изучать математику и физику. Работая с пособием, ты тоже, затрачивая совсем немного времени, сможешь легко вести математические преобразования физических формул, как при изучении нового материала, так и при решении задач. Пособие выполнит своё предназначение, когда ты сможешь без него обходиться. В этом случае используй пособие как справочник, а также для повторения и запоминания формул.

Пособие состоит из трёх разделов:

I. Состав физических формул и нахождение величин из формул.

II. Работа с формулами при решении задач по физике.

III. Контрольные задачи.

Если работу с первым разделом можно начинать с седьмого класса, то работу со вторым разделом следует отложить примерно до начала восьмого класса.

Раздел I состоит из подразделов:

1. таблиц алфавитов;
2. основной таблицы, где представлено большинство, объединённых в группы, формул, которые изучаются в курсе физики с 7-го по 11-й классы, и их замены на формулы математические;
3. таблицы с алгоритмами – последовательными правилами – работы с той или иной группой формул.

К большинству подразделов даны пояснения и краткие сведения из курса математики.

Работа с пособием начинается с нахождения в основной таблице раздела I изучаемой на уроке формулы. Данную формулу необходимо выделить, проведя по ней специальным фломастером. Такие фломастеры дают прозрачную широкую линию ненасыщенного цвета. В результате изученная формула будет выделена и читаема.

Далее, в специально заведённой тетради, самостоятельно выполни упражнения по выражению всех величин, кроме числовых коэффициентов, входящих в данную формулу. К примеру, если изучается формула 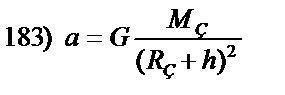, ты должен последовательно найти 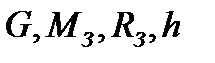, считая, что остальные величины, входящие в формулу, становятся известны. При затруднениях обращаешься к таблице с алгоритмами в подразделе 3, учителю. Чтобы закрепить навык работы с данной формулой, можно использовать и формулы из одной с ней группы, которые ещё только будут изучаться в дальнейшем. Эта простая, но необходимая работа, позволит тебе довести навыки нахождения величин до «автоматизма». Останавливайся только тогда, когда нахождение всех величины, входящих в данную группу формул, не будет вызывать трудностей.

Если в изучаемой формуле встречается буква греческого алфавита, потренируйся в написании буквы. Каждую новую букву греческого алфавита следует написать не менее двадцати раз. Для тренировки выдели пару страниц в конце своей тетради.

После рассмотрения задач раздела II, самостоятельно воспроизведи в тетради каждое решение. При решении задач, предлагаемых учителем, обращай внимание на «математику», находи соответствие между задаваемыми задачами и задачами раздела II.

Физика «говорит» на языке математики, ты свободно «заговоришь» на этом языке, и только в этом случае поймёшь, О ЧЁМ «говорит» физика. Тогда объяснения учителя на уроке окажутся на удивление простыми, а физика – увлекательнейшей наукой, изучение которой принесёт тебе не муки зубрёжки, а радость открытия новых знаний.

Надеюсь, пособие будет твоим верным помощником на протяжении нескольких лет. Удачи, уверенности в своих силах и хороших оценок тебе!

 

РАЗДЕЛ I. Состав физических формул и нахождение величин из формул.

Алфавиты.

Латинский алфавит знаком тебе по урокам иностранного языка. В физических формулах задействованы все буквы этого алфавита – как заглавные, так и строчные. Очень часто используется рукописный вариант букв, который в таблице не представлен.

 

Латинский алфавит.

Печатные буквы	Название букв	Печатные буквы	Название букв
Заглавные	Строчные		Заглавные	Строчные
A	a	а	N	n	эн
B	b	бе	O	o	о
C	c	це	P	p	пэ
D	d	де	Q	q	ку
E	e	е	R	r	эр
F	f	эф	S	s	эс
G	g	жэ (ге)	T	t	тэ
H	h	аш	U	u	у
I	i	и	V	v	вэ
J	j	жи	W	w	дубль-вэ
K	k	ка	X	x	икс
L	l	эль	Y	y	игрэк
M	m	эм	Z	z	зэт

 

Буквы греческого алфавита в школьном курсе математики используются не так широко, а в курсе физики наравне с латинскими буквами. Это создаёт определённые трудности, поскольку греческий язык в школе не изучается. Греческий алфавит - основа русского алфавита.

В школьном курсе физики используется только часть греческого алфавита. Различие между печатными и рукописными буквами отсутствует. Если ты затрудняешься написать греческую букву, попроси учителя показать.

 

Греческий алфавит.

Печатные буквы	Название букв	Печатные буквы	Название букв
Заглавные	Строчные		Заглавные	Строчные
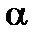
		альфа			ню
	β	бета		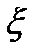	кси
		гамма			омикрон
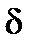
		дельта			пи
		эпсилон		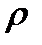	ро
		дзета		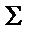	сигма
		эта		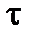	тау
	θ	тэта			ипсилон
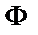
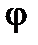
		йота			фи
		каппа			хи
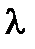
		ламбда		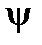	пси
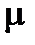
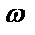
		мю			омега

Таблица физических формул и их математического представления.

Все физические формулы разделены по сложности на группы A, B, C, D, E. Разновидности формул внутри группы пронумерованы. В каждой формуле, математически представляющей физическую формулу, указаны знаки умножения и восстановлены скобки у большинства многочленов.

ОДНОЧЛЕНАМИ называют ПРОИЗВЕДЕНИЯ чисел, переменных, их степеней, а также числа, переменные и их степени.

Например,

5а²х,

2b³(-3),

-3a⁷,

xy²,

-7,

2³,

х,

х⁴ – одночлены.

МНОГОЧЛЕНОМ называется СУММА одночленов.

Имеется в виду АЛГЕБРАИЧЕСКАЯ сумма.

Например,

5а²х + 2b³(-3) + (-3a⁷) и

xy² + (-7) + 2³ + х + х⁴ - многочлены.

В столбце математического представления физических формул одночлены записаны так: ;

а многочлены так: .

В столбце «Физические формулы» представлено большинство формул, которые изучаются в школе. Формулы отдельно пронумерованы. Порядок следования формул никак не связан с изучаемыми в курсе физики разделами. Этот порядок определяется усложнением формулы, появлением дробей, квадратов и корней величин, многочленов, а также надчёркиваний и индексов, их количеством и длиной.

В столбце «Пояснения к формулам» в неочевидных случаях показано, почему данная формула отнесена именно к этой группе.

Следует помнить, что одни и те же буквы – как R, t, F, U и т.д. – в разных разделах физики обозначают разные физические величины.

 

№ г р у п п ы	Математическое представление формул	№ ф о р м у л ы	Формулы физики	Пояснения к формулам
		,
		,
		,

---

12345Следующая ⇒

Поделиться с друзьями:

---

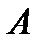
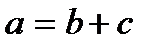
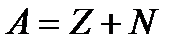
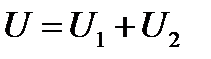
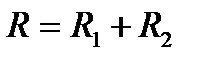
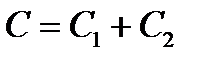
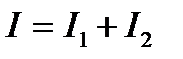
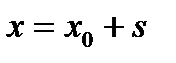
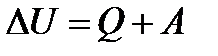
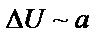
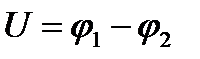
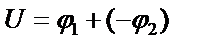
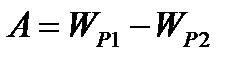
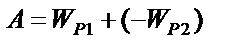
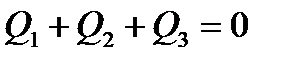
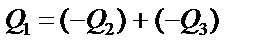
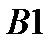
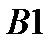
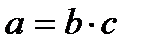
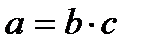
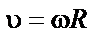
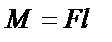
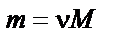
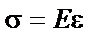
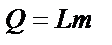
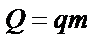
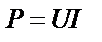
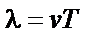
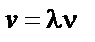
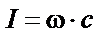
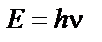
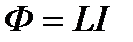
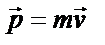
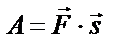
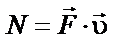
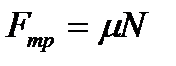
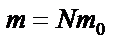
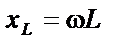
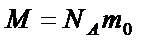
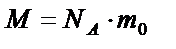
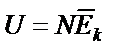
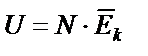
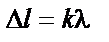
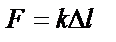
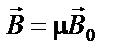
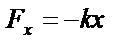
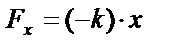
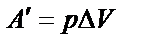
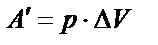
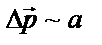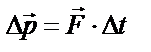
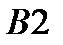
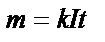
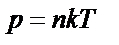
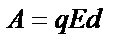
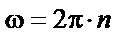
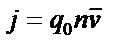
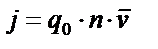
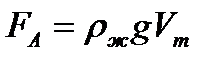
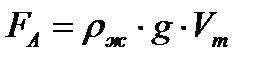
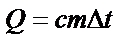
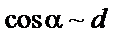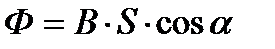
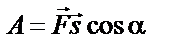
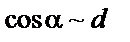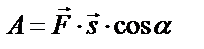
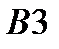
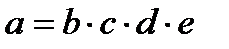
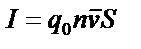
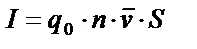
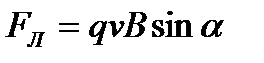
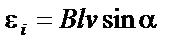
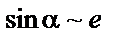
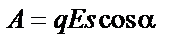
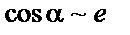
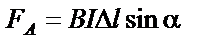
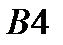
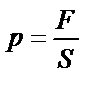
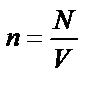
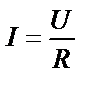
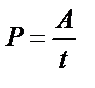
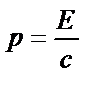
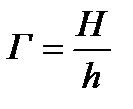
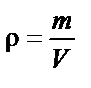
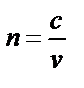
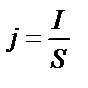
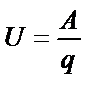
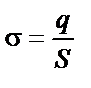
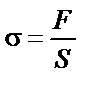
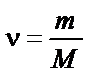
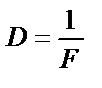
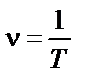
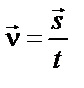
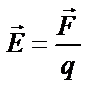
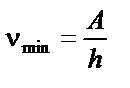
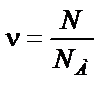
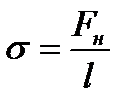
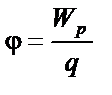
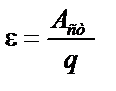
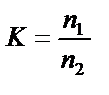
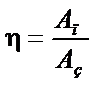
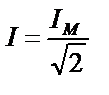
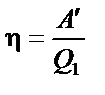
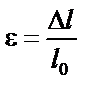
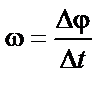
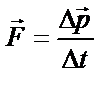
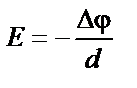
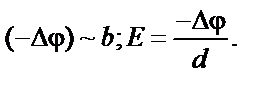
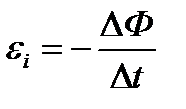
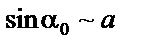
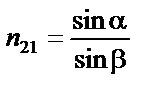
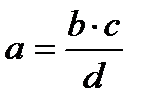
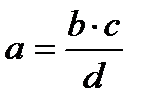
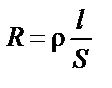
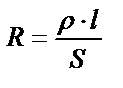
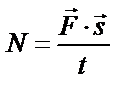
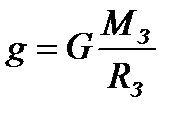
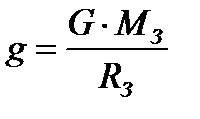
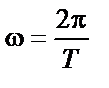
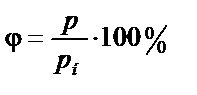
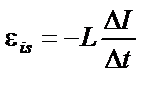
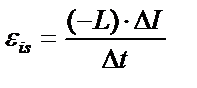
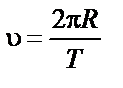
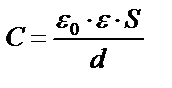
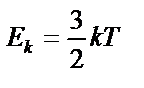
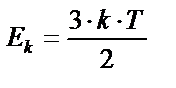
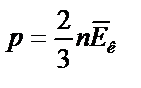
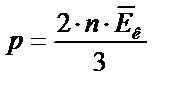
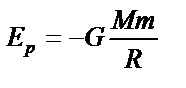
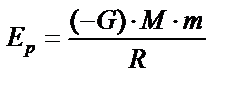
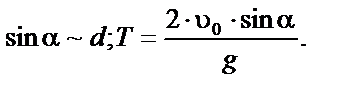
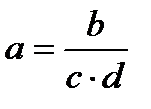
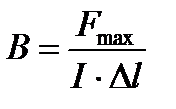
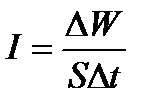
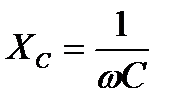
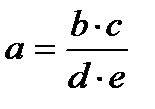
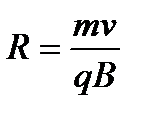
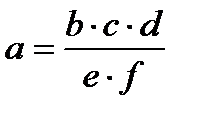
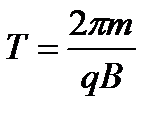
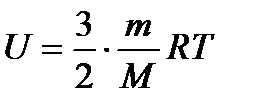
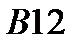
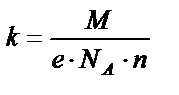
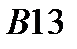
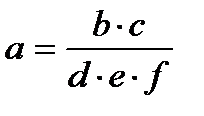
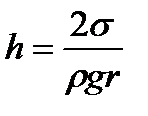
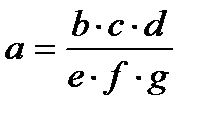
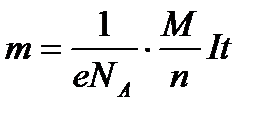
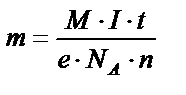
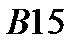
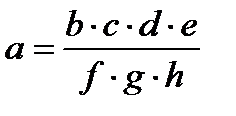
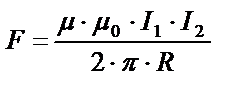
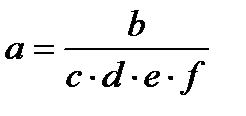
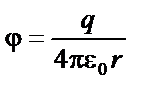
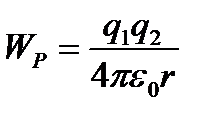
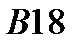
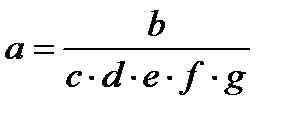
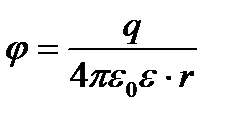
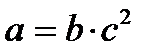
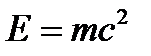
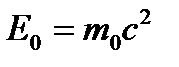
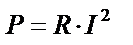
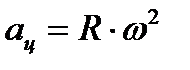
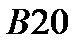
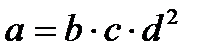
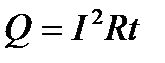
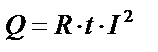
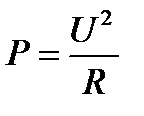
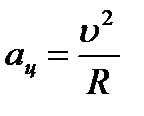
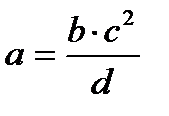
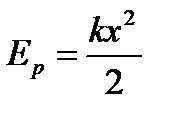
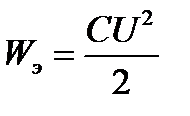
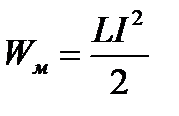
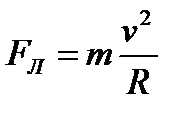
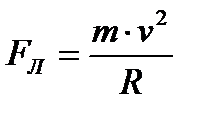
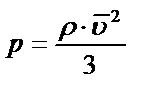
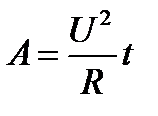
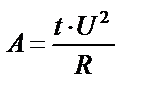
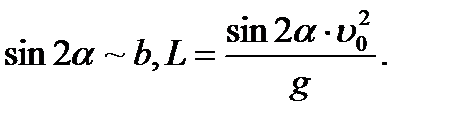
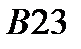
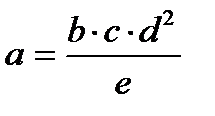
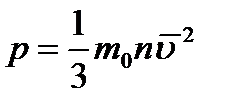
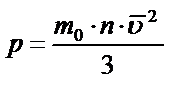
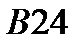
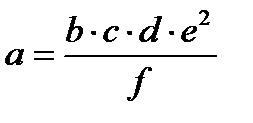
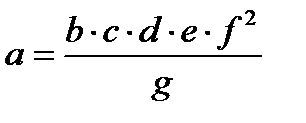
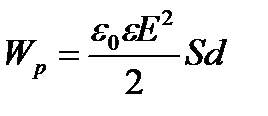
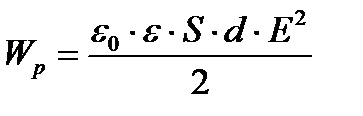
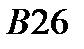
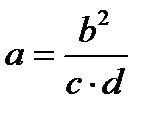
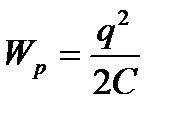
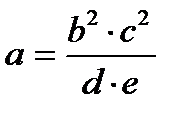
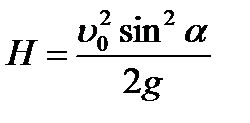
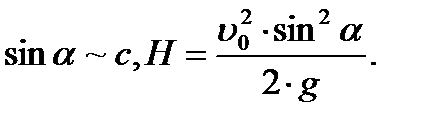
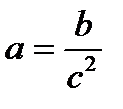
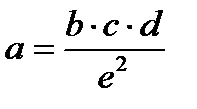
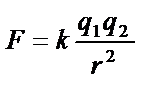
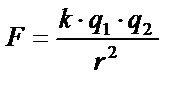
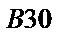
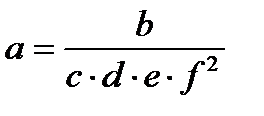
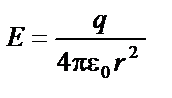
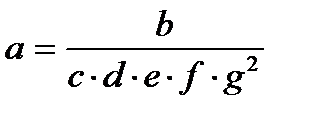
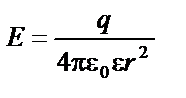
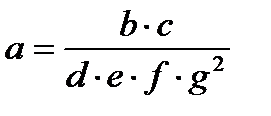
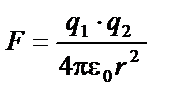
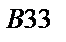
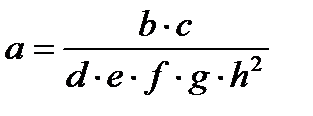
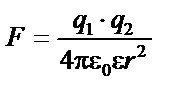
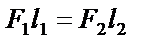
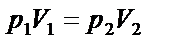
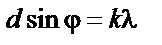
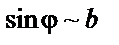
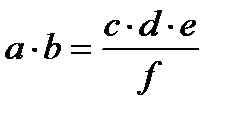
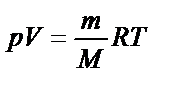
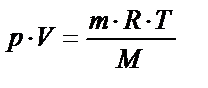
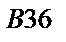
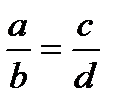
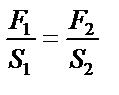
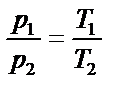
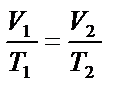
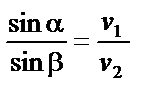
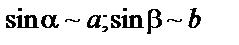
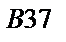
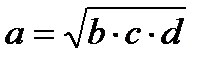
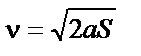
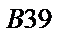
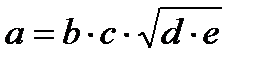
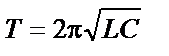
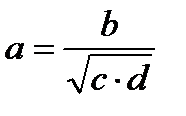
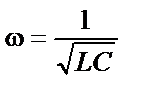
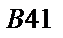
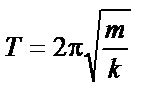
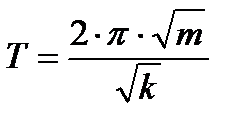
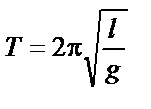
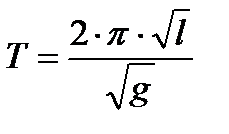
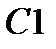
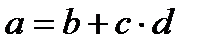
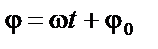
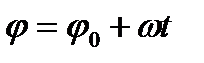
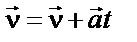
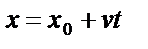
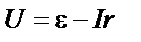
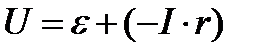
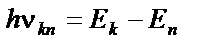
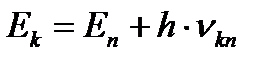
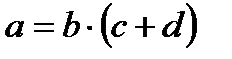
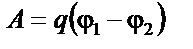
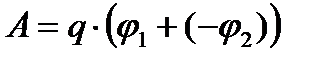
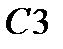
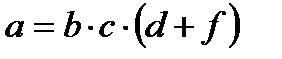
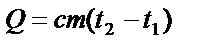
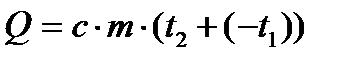
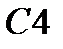
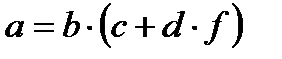
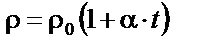
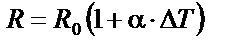
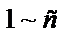
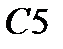
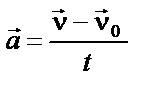
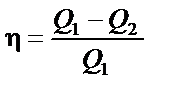
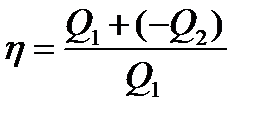
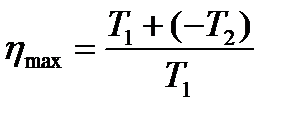
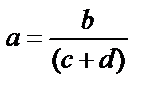
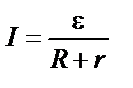
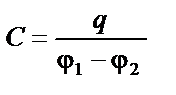
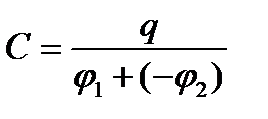
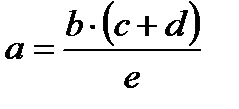
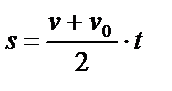
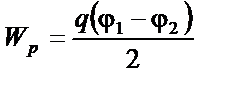
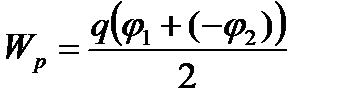
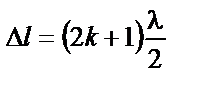
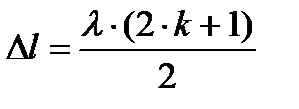
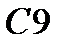
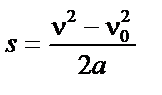
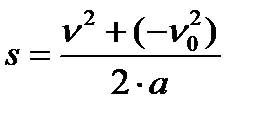
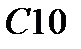
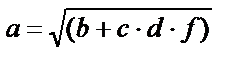
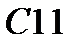
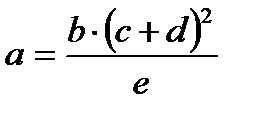
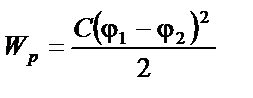
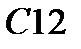
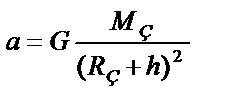
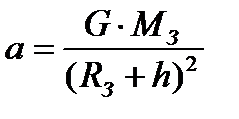
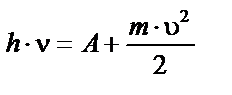
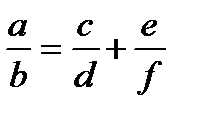
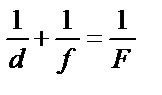
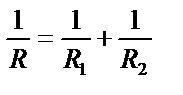
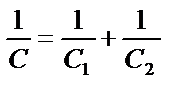
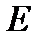
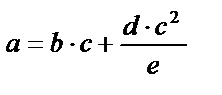
Дата добавления: 2016-11-20; Мы поможем в написании ваших работ!; просмотров: 1369 | Нарушение авторских прав

---

Лучшие изречения:

© 2015-2024 lektsii.org - Контакты - Последнее добавление