Пусть требуется сложить дроби 
. Приведем эти дроби к общему знаменателю bd. Для этого числитель и знаменатель первой дроби умножим на d, а числитель и знаменатель второй дроби умножим на b. Получим:
.
Теперь можно воспользоваться правилом сложения дробей с одинаковыми знаменателями:
.
В этой группе формул часто требуется умножить одночлен на многочлен или вынести общий множитель за скобки.
При умножении одночлена на многочлен пользуются правилом:
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
То есть: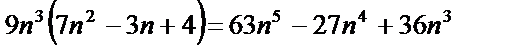 
.
При вынесении общего множителя за скобки необходимо предварительно разложить многочлен на множители.
Рассмотрим многочлен 
. Каждый его член можно заменить произведением двух множителей, один из которых равен 3b:
.
Полученное выражение на основе распределительного свойства умножения можно представить в виде произведения двух множителей. Один из них — общий множитель 3b, а второй — сумма 2a2 и 5b:
.
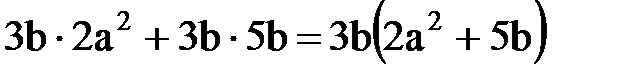Итак,
.
При работе с формулами за скобки выносят общий множитель, который выступает искомой величиной.
| Алгоритм преобразований | Исходная и преобразованные формулы. | Пример поиска искомой величины в физической формуле. |
| 
| |
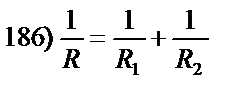
| 1.Привести дроби к общему знаменателю. | 
| 
|
| 2.Сложить дроби с общим знаменателем. |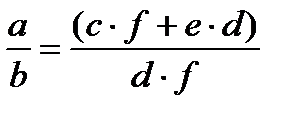 
| 
|
| 3.Освободиться от знаменателя(лей) (в случае пропорции, перемножив её крайние и средние члены). |
| 
|
| 4. Если искомая величина встречается только в одной части равенства, найти её, следуя пунктам 2C – 11C. |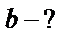 
Следуя тем же пунктам, можно найти и  .
| 
|
| 5.Если искомая величина встречается в обеих частях равенства, умножить в правой части одночлен на многочлен. | 
Из
следует,
| 
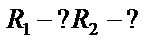Из
следует,
|
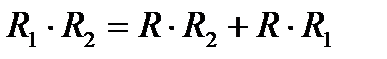
| 6. Сгруппировать сомножители с искомой величиной в одной – любой – части равенства, меняя при переносе знак одночленов на противоположный. | 
Из
следует
| 
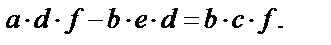
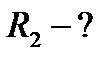В
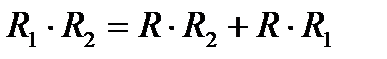перенесём одночлены с  в левую часть:
|
| 7.Вынести искомую величину за скобки. | 
| 
|
| 8. Найти искомую величину, поделив обе части равенства на многочлен – сомножитель искомой величины. | 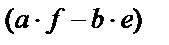 –многочлен, сомножитель  .
|  – сомножитель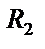 
|
Группа E. В группе E для одной величины требуется решение квадратного уравнения.
| Алгоритм преобразований | Исходная и преобразованные формулы. | Пример поиска искомой величины в физической формуле. |
| 
| |
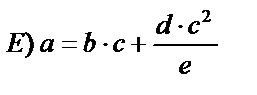
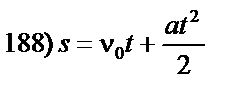
1.Величины  находить по алгоритму группы  .
| ||
2.Для нахождения  представить равенство в стандартном для квадратного уравнения виде
 , перенеся все одночлены со сменой знака в одну часть равенства.
| 
Или
 ,
 ,
 ,
|
|
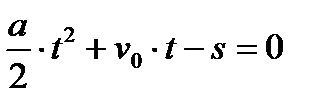
3.Решить квадратное уравнение.
|
|  
|
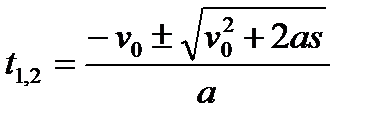
