Дзета. Начинать? Зачем я должен начинать? Мой ум не пуст, когда я открываю (или изобретаю) задачу.
Учитель. Не дразните Бету. Вот задача: имеется ли соотношение между числами вершин, ребер и граней многогранника, аналогичное тривиальному соотношению между числами вершин и сторон многоугольника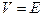 
?[122]. Как вы приметесь за эту задачу?
Дзета. Прежде всего я не имею стипендии от правительства Для производства подробной описи многогранников, а также не обладаю армией ассистентов для подсчета их вершин, ребер и граней и составления таблиц по этим данным. Но если бы даже все это у меня было, я не имел бы терпения – или интереса – испытывать пригодность одной формулы за другой.
Бета. Что же тогда? Вы ляжете на диван, закроете глаза и забудете о данных?
Дзета. Так точно я и сделаю. Чтобы начать, мне нужна идея, а не какие-либо данные.
Бета. А откуда вы возьмете идею?
Дзета. Она уже имеется в нашем уме, когда мы формулируем задачу; фактически она имеется уже в самой формулировке задачи.
Бета. Какая же идея?
Дзета. Та, что для многоугольника .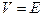
Бета. Ну так что же?
Дзета. Задача никогда не приходит с неба. Она всегда связана с нашим земным знанием. Мы знаем, что для многоугольников 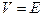. Теперь многоугольник есть система многоугольников, состоящая из одного единственного многоугольника. Многогранник есть система многоугольников, состоящих более чем из одного многоугольника. Но для многогранников 
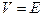. В каком пункте отношение отказалось служить при переходе от монополигональных систем к полиполигональным? Вместо того чтобы собирать данные, я прослежу, как эта задача возникла на основе нашего земного знания, или каковы были ожидания, опровержение которых представило эту задачу.
Рис. 17
Сигма. Правильно. Последуем вашим рекомендациям. Для всякого многоугольника 
(рис. 17, а). Что случится, если я прикреплю к нему другой многоугольник (необязательно в той же плоскости)? Добавляемый многоугольник имеет n 1 сторон и n 1 вершин; если мы прикрепим его к первоначальному по цепочке из 
ребер и 
вершин, то мы увеличим число ребер на 
, а число вершин на 
; значит, в новой 2‑полигональной системе получится избыток в числе ребер над числом вершин 
(рис. 17, б); необычное, но совершенно допустимое прикрепление мы видим на рис. 17, в. «Прикрепление» новой грани к системе будет всегда увеличивать этот избыток на единицу; следовательно, для построенной таким образом F ‑полигональной системы будет всегда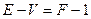 
.
Бета. Или 
.
Ламбда. Но ведь это неверно для большей части полигональных систем. Возьмите куб…
Сигма. Но мое построение может привести только к «открытым» полигональным системам – ограниченным цепочкой ребер. Мой мысленный эксперимент я могу легко распространить на «закрытую» полигональную систему без такой границы. Это закрытие может быть произведено, если мы такую сосудообразную систему покроем многоугольником – крышкой; прикрепление такого покрывающего многоугольника увеличит F на единицу без изменения V или E …
Рис. 18
Рис. 19
Дзета. Итак, для закрытой полигональной системы – или закрытого многогранника, – построенной таким образом,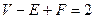 
; догадка, которую мы теперь получили без «наблюдения» числа вершин, ребер и граней одного многогранника!
Ламбда. И теперь вы можете применить метод доказательств и опровержений без какой-нибудь «индуктивной отправной точки».
Дзета. С той разницей, что вам уже не надо будет выдумывать доказательство – оно уже получилось готовым. Вы можете продолжать непосредственно с опровержениями, анализом доказательства, образованием теоремы.
Ламбда. Тогда в вашем методе – вместо наблюдений – доказательство предшествует наивной догадке[123].
Дзета. Ну, я не назвал бы «наивным» предположение, которое выросло из доказательства. В моем методе нет места для индуктивных наивностей.
Бета. Есть возражение! Вы только отодвинули назад наивное индуктивное начало: вы же начали с «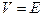 для многоугольников». Разве вы не основываете это на наблюдениях?
Дзета. Как большинство математиков, я не умею считать. Я только что попытался сосчитать стороны и вершины у семиугольника; сначала я нашел 7 сторон и 8 вершин, а затем, второй раз, 8 сторон и 7 вершин…
Бета. Шутки в сторону, как вы получили ?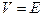
Дзета. Я был глубоко потрясен, когда впервые понял, что для треугольника . Я, конечно, хорошо знал, что для одного ребра (рис. 18, a). Я знал также, что присоединение новых ребер всегда увеличивает на единицу и число ребер и число вершин (рис. 18, b и 18, c). Почему же тогда в полигональных системах ребер будет ? Потом я понял, что это получается вследствие перехода от открытой системы ребер (которая ограничивается двумя вершинами) к закрытой системе ребер (которая не имеет такой границы), так как мы «закрываем» открытую систему, вставляя ребро без добавления повой вершины. Таким образом, я доказал, но не наблюдал, что для многоугольников будет .
Бета. Ваша хитрость не поможет вам. Вы только еще дальше отодвинули назад индуктивную отправную точку; теперь обратимся к утверждению, что для всякого ребра . Вы это доказали или наблюдали?
Дзета. Я доказал это. Я, конечно, знал, что для одной вершины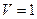 
(рис. 19). Моей задачей было построить аналогичное соотношение…
Бета (яростно). Разве вы не наблюдали, что для точки ?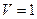
Дзета. А вы наблюдали это? (В сторону, к Пи.) Должен ли я сказать ему, что моей «индуктивной отправной точкой» было пустое пространство? Что я начал с того, что «наблюдал» ничто?
Ламбда. Во всяком случае два пункта мы установили. Сначала Сигма аргументировал, что только благодаря исторической случайности можно прийти к наивной индуктивной догадке; если имеешь перед собой реальный хаос фактов, то вряд ли сможешь подвести их под изящную формулу. Затем Дзета показал, что для логики доказательств и опровержений мы совсем не нуждаемся ни в наивной догадке, ни в индуктивистской отправной точке.
Бета. Возражение! А как быть с теми прославленными наивными догадками, которым не предшествовали (или даже за которыми не следовали) доказательства, вроде догадки о четырех цветах, которая говорит, что четырех цветов вполне достаточно для того, чтобы раскрасить любую карту, или догадки Гольдбаха? Ведь только благодаря историческим случайностям доказательства могут предшествовать теоремам, или может иметь место «дедуктивная догадка» Дзеты; в других случаях первыми бывают наивные индуктивные догадки.
Учитель. Мы, конечно, должны усвоить оба эвристических образца; дедуктивная догадка является самой лучшей, но наивная догадка лучше, чем отсутствие всякой догадки. Но наивная догадка не индукция; такие вещи, как индуктивные догадки, не существуют!
Бета. Но ведь мы нашли наивную догадку при помощи индукции! «Это значит, что она была внушена наблюдением, указана особыми событиями… И среди частных случаев, которые мы рассмотрели, мы могли различить две группы: те, которые предшествовали формулировке догадки, и те, которые появились потом. Первые подсказали догадку, вторые поддержали ее. Оба ряда случаев произвели некоторого рода контакт между догадкой и «фактами»…[124] Этот двойной контакт и представляет сердце индукции; первый создает индуктивную эвристику, второй дает индуктивное оправдание, или индуктивную логику.
Учитель. Нет! Факты не подсказывают догадок и тем более не поддерживают их!
Бета. Тогда что же подсказало мне 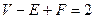, если не факты, собранные в моей таблице?
Учитель. Я скажу вам. Вам самим несколько раз не удавалось подвести их под формулу[125]. Произошло следующее: у вас были три или четыре догадки, которые по очереди были быстро отвергнуты. Ваша таблица была построена в процессе проверки и опровержения этих догадок. Эти мертвые и теперь уже забытые догадки подсказали факты, а не факты подсказали догадки. Наивные догадки не являются индуктивными догадками; мы приходим к ним путем испытаний и ошибок, через предположения и опровержения»[126]. Но если вы думаете – неправильно, – что пришли к ним индуктивным путем от ваших таблиц, если вы верите, что чем длиннее таблица, тем больше догадок она подскажет и потом поддержит, то вы можете потратить даром свое время, собирая ненужные данные. Таким образом, проникшись доктриной, что путь открытия ведет от фактов к догадкам и от догадки к доказательству (миф индукции), вы можете полностью забыть об эвристической альтернативе: дедуктивном угадывании[127].
Математическая эвристика очень похожа на научную эвристику – не потому, что обе являются индуктивными, но потому, что обе характеризуются догадками, доказательствами и опровержениями. Важная разница заключается в природе соответствующих догадок, доказательств (в науке – объяснений) и контрапримеров[128].
Бета. Я вижу. Тогда наша наивная догадка никогда не была первой догадкой, «подсказанной» жесткими непредположительными фактами; ей предшествовали многие «донаивные» догадки и опровержения. Логика догадок и опровержений не имеет исходной точки, но логика доказательств и опровержений имеет ее: она начинается с первой наивной догадки, за которой должен последовать мысленный эксперимент.
Альфа. Может быть. Но тогда я не стал бы называть ее «наивной»[129].
Каппа (в сторону). Даже в эвристике нет такой вещи, как совершенная наивность.
Бета. Главная вещь заключается в том, чтобы как можно скорее выйти из периода испытаний и ошибок, быстро перейти к мысленным экспериментам, не имея слишком много «индуктивного» уважения к «фактам». Это уважение может задерживать рост знания. Представьте себе, что при помощи испытаний и ошибок вы пришли к догадке 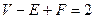и что она будет сразу же отвергнута наблюдением: для картинной рамы 
. Если вы слишком уважаете факты, в особенности когда они опровергают ваши догадки, вы пойдете снова к до-наивным испытаниям и ошибкам и будете искать другую догадку. Но если вы обладаете лучшей эвристикой, то вы по крайней мере попытаетесь игнорировать неприятное испытание наблюдением и попробуете испытание мысленным экспериментом, вроде доказательства Коши.
Сигма. Какая путаница! Зачем называть испытанием доказательство Коши?
Бета. Зачем называть испытанием доказательство Коши? Это было испытание! Послушайте. Вы начали с наивной догадки: 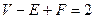для всех многогранников. Затем вы отсюда вывели следствие: «если наивная догадка справедлива, то после устранения одной грани для оставшейся сети будет »; «если это следствие справедливо, то , даже после триангуляции»; «если это последнее следствие справедливо, то будет справедливым, когда мы будем отнимать треугольники по одному»; «если это верно, то для одного единственного треугольника»…
Теперь это последнее заключение оказалось общеизвестным, истинным. Но что произошло бы, если бы мы заключили, что для единственного треугольника ? Мы сразу же отвергли бы первоначальное предположение как ложное. Все, что мы сделали, сводится к тому, что мы испробовали нашу догадку, а именно выводили из нее следствия. Испытание, по-видимому, подтвердило нашу догадку. Но подтверждение еще не доказательство.
Сигма. Но тогда наше доказательство доказало даже еще меньше, чем мы думали! Тогда нам нужно обратить процесс и попытаться построить мысленный эксперимент, который идет в противоположном направлении: от треугольника назад к многограннику!
Бета. Это верно. Только Дзета показал, что вместо решения нашей задачи сначала путем создания наивной догадки при помощи испытаний и ошибок, затем проверки, затем обращения испытания в доказательство можно сразу же начать с реального доказательства. Если бы мы поняли возможность дедуктивного угадывания, то мы могли бы избежать всей этой псевдоиндуктивной возни!
Каппа (в сторону). Что за драматическая серия поворотов на 180°! Критически настроенный Альфа обратился в догматика, догматик Дельта в опровергателя, а теперь индуктивист Бета в дедуктивиста!
Сигма. Но подождите. Если за испытательным мысленным экспериментом…
Бета. Я назову его анализом…
Сигма…может всегда сразу последовать доказательный мысленный эксперимент…
Бета. Я назову его синтезом…[130]
Сигма. …то будет ли «аналитическая теорема» необходимо тождественной с «синтетической». Идя в противоположном направлении, мы можем пользоваться другими леммами[131].
Бета. Если они будут другими, то синтетическая теорема должна заменить аналитическую; в конце концов анализ только испытывает, тогда как синтез доказывает.
Учитель. Ваше открытие, что наше «доказательство» фактически было испытанием, как будто шокировало класс и отвлекло его внимание от вашего главного аргумента: именно, если мы имеем догадку, уже опровергнутую контрапримером, то мы должны отложить опровержение в сторону и попытаться испробовать догадку при помощи мысленного эксперимента. Таким путем мы могли бы напасть на доказательство, оставить фазу испытаний и ошибок и пустить в ход метод доказательств и опровержений. Но ведь именно это и заставило меня сказать, что «я готов заняться “доказательством” ложного предположения»[132]. И тогда Ламбда потребовал в своем
Правиле 1: «Если вы имеете какую-нибудь догадку, то попробуйте доказать ее и опровергнуть ее».
Дзета. Это верно. Но позвольте мне дополнить правило Ламбды и Правило 4 Омеги так:
Правило 5. Если у вас есть контрапример любого типа, попробуйте при помощи дедуктивного гадания найти более глубокую теорему, для которой уже более не будет контрапримеров.
Омега. Вы теперь расширяете мое понятие «глубины» и, может быть, вы и правы. Но как же быть с действительным применением нашего нового правила? До сих пор оно только давало нам результаты, которые мы уже знали. Легко быть мудрым после события. Ваше «дедуктивное гадание» как раз представляет синтез, соответствующий первоначальному анализу Учителя. Но теперь вы должны быть честным – вы должны использовать ваш метод для нахождения догадки, которой вы еще не знали, с обещанным увеличением содержания.
Дзета. Правильно. Я начну с теоремы, рожденной моим мысленным экспериментом: «Все закрытые нормальные многогранники будут эйлеровыми».
Омега. «Нормальные»?
Дзета. Я не желаю тратить времени на прохождение через метод доказательств и опровержений. Я просто называю «нормальными» все многогранники, которые могут быть построены, исходя из «совершенного» многоугольника, прикладывая к нему (а) первые 
граней без изменения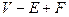 
(это будут открытые нормальные многогранники) и (б) наконец, закрывающую грань, которая увеличивает 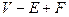на 1 (и превращает открытый многогранник в закрытый).
Омега. «Совершенный» многоугольник?
Дзета. Под «совершенным» многоугольником я подразумеваю такой, который может быть построен, исходя из одной-единственной вершины, прикладыванием к ней сначала 
ребер без изменения 
и, наконец, последнего закрывающего ребра, которое уменьшает на 1.
Омега. Будут ли ваши закрытые нормальные многогранники совпадать с многогранниками Коши?
Дзета. Я не желаю сейчас углубляться в это.
