Если есть основания предполагать, что исследуемая зависимость двух величин Y и X является линейной, то есть удовлетворяет формуле
, (10.1)
и экспериментальный график зависимости y (x) это подтверждает, то есть через доверительные интервалы всех экспериментальных точек можно провести прямую линию, то по результатам измерения величин Y и X, то есть по значениям координат экспериментальных точек, можно определить параметры линейной зависимости k и b. Это можно сделать по крайней мере двумя способами.
Первый способ – графический.
· Надо провести прямую линию на графике так, чтобы она пересекла доверительные интервалы всех точек и при этом как можно ближе прошла ко всем точкам. После этого можно приступить к определению k и b.
· k представляет собой угловой коэффициент прямой, поэтому его можно найти как отношение приращения функции D y к приращению аргумента D x. В качестве D x удобнее всего выбрать разность координат крайних точек графика (x n – x 1). При этом D y = y (x n) – y (x 1).
 |
Графический способ определения параметров прямой линии
Рис.5
Обратите внимание: y (x 1) и y (x n) – это не ординаты экспериментальных точек y 1 и y n, физической величины Y, которые получены до построения графика зависимости y (x). Это значения линейной функции y (x), которую изображает проведённая на графике прямая.
· b – это отрезок, который прямая линия графика отсекает на оси ординат (на вертикальной оси), поэтому для нахождения b надо довести экспериментальную прямую до оси ординат и определить ординату их точки пересечения. Но это правило справедливо только в том случае, когда координатные оси пересекаются в начале координат, то есть в точке с координатами (0; 0). Если же удобнее выбрать другую точку пересечения осей, как это сделано при построении графика на рис.5, то нужно использовать другое правило: надо выбрать две точки на прямой, например, точки с координатами (x 1; y (x 1)) и (x n; y (x n)) и записать уравнение прямой, проходящей через эти точки:
. (10.2)
Приведение этого уравнение к виду (10.1) даёт следующее выражение для b:
. (10.3)
Описанный метод определения параметров прямой линии k и b есть метод их косвенного измерения. А так как всякое измерение обладает погрешностью, то возникает вопрос: как оценить погрешности D(k) и D(b)? Проще всего это сделать так.
· Надо провести через доверительные интервалы ещё две прямые линии: для первой из них параметры k и b должны быть максимально возможными, поэтому её надо провести как можно круче и выше, для второй – значения k и b должны быть минимально возможными, её надо провести как можно полого и ниже.
· После этого погрешности D(k) и D(b) можно определить очевидным образом:
(10.4)
Второй способ определения параметров линейной зависимости, полученной экспериментальным путём, – аналитический.
Он называется методом наименьших квадратов. Его идея в том, что среди всевозможных комплектов пары чисел k и b существует такой единственный комплект, для которого сумма квадратов отклонений ординат экспериментальных точек от соответствующих ординат прямой линии с параметрами k и b, минимальна. Не рассматривая этот метод в деталях, приведём конечные выражения, позволяющие определить k и b.
(10.2)
где обозначено:
(10.3)
В этих формулах n – число экспериментальных точек, а наборы чисел (x i) и (y i) – результаты измерений, то есть абсциссы и ординаты экспериментальных точек.
Проделав вычисления по формулам (10.2) – (10.3), следует сделать проверку. Для этого надо по формуле (10.1) вычислить значения ординат прямой линии при двух произвольных значениях x, например при x 1 и при x n, затем нанести на график две контрольные точки, то есть точки с координатами (x 1, y (x 1)) и (x n, y (x n)), и соединить их прямой линией. Если все вычисления проделаны верно, то прямая автоматически пройдёт оптимальным образом, то есть пересечёт доверительные интервалы всех экспериментальных точек и при этом будет максимально приближена к экспериментальным точкам.
Погрешности косвенного измерения параметров прямой линии k и b методом наименьших квадратов определяются по следующим формулам:
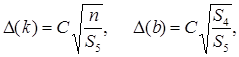(10.4)
где
. (10.5)
Литература
1. Зайдель А.Н. Погрешности измерений физических величин. -Л.: Наука, 1985. – 110 с.
2. Рабинович С.Г. Погрешности измерений. Л.: Энергия, 1978. -258 с.
[1] Число измерений в серии n называется объёмом серии.
