| Вид функции x (a, b, c,...) | Абсолютная погрешность D(x) | Относительная погрешность e(x) |
| x = a ± b | 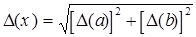
| 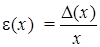
|
| x = a ± b ± c | 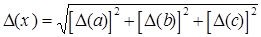
| 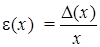
|
x = ab, 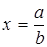
| D(x) = x e(x) | 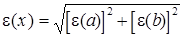
|
x = abc, 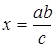 , , 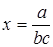
| D(x) = x e(x) | 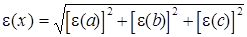
|
Замечание. Приведённые в этом пункте формулы справедливы для всех типов погрешностей – для приборных, случайных и полных. Чаще всего их используют для полных погрешностей – сначала находят приборные, случайные и полные погрешности всех прямых измерений, а затем – полную погрешность косвенного измерения.
8. Округление погрешностей и результатов измерений.
Запись результата измерений
Термин “ оценка погрешности ” означает, что нет смысла высчитывать погрешность с большой точностью. Следует определить лишь первую значащую цифру, так как знание погрешности нужно, главным образом, для того, чтобы определить тот предельный разряд K 0 результата измерения, в котором содержится ошибка. Цифры в разрядах, старших K 0, являются достоверными, а в разрядах, младших K 0, – недостоверными. Разряд K 0 занимает пограничное положение: цифра в этом разряде частично достоверна, её неопределённость как раз и показывает первая значащая цифра погрешности.
Из этого вытекает следующее правило округления.
Погрешность нужно округлять до единственной значащей цифры, а результат измерения – до предельного разряда K 0, равного тому разряду, в котором находится единственная значащая цифра погрешности.
Пример. Проведено косвенное измерение давление газа в электронной лампе. Результат измерения: p = 35,27 Па, оценка погрешности измерения дала: D(p) = 2,15 Па. Эти данные следует округлить так: D(p) = 2 Па, p = 35 Па. Предельный разряд K 0 в этом примере – это младший разряд целой части, то есть разряд единиц.
Результат измерения принято записывать вместе с его гарантией, то есть вместе с погрешностью. Образец формы записи следующий:
p = (35 ± 2) Па, e(p) = 6%.
Другие примеры записи результатов измерений:
I = (17,3 ± 0,3) мА, e(I) = 2%.
v = (848,7 ± 0,5)×10-4 м/с, e(v) = 0,06%.
Построение графиков
Результат экспериментального исследования зависимости одной величины от другой очень наглядно иллюстрирует график зависимости. Рассмотрим для примера график, изображённый на рис. 4.
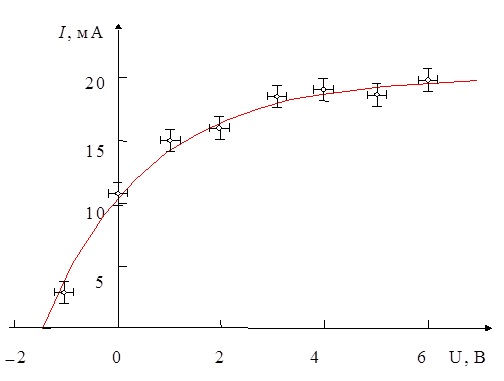 |
Вольтамперная характеристика фотодиода
Рис. 4
На этом рисунке вольтамперная характеристика, то есть кривая зависимости силы тока на анод I от напряжения между анодом и катодом U, выглядит в виде плавно изогнутой линии, которая с ростом напряжения постепенно превращается в прямую, параллельную оси абсцисс (оси напряжения), отражая явление насыщения фототока. Построена эта линия по восьми экспериментальным точкам, причём только одна из точек лежит на кривой. Но это вполне допустимо. Дело в том, что экспериментальная точка представляет собой два результата измерения – напряжения и тока. Каждый из этих результатов обладает погрешностью, эти погрешности и изображены около каждой точки в виде двух доверительных интервалов с центрами в экспериментальной точке: вертикальный интервал – это доверительный интервал результата измерения силы тока, его ширина равна 2D(I), горизонтальный интервал – это доверительный интервал результата измерения напряжения, его ширина равна 2D(U). Так как доверительный интервал, согласно определению 1, есть множество возможных результатов измерения, то кривую зависимости I (U) совсем не обязательно проводить строго через экспериментальные точки, достаточно, чтобы эта кривая прошла через доверительные интервалы всех экспериментальных точек.
Итак, последовательность действий при построении графика такова.
· Выбрать рациональный масштаб величин, изображаемых на графике, так чтобы экспериментальные точки разместились на всей площади графика, а не в какой-то небольшой её части.
· Начертить оси графика и расставить на них масштабные метки. Метки должны располагаться на одном и том же расстоянии друг от друга и не слишком часто, чтобы не загромождать рисунок. Рядом с метками надо проставить опорные числа – значения величин, соответствующих масштабным меткам. Разрешается, чтобы отличие соседних опорных чисел друг от друга было таким: (1; 2; 5) единиц, или (0,1; 0,2; 0,5) единиц, или (10; 20; 50) единиц и так далее. Опорные числа можно проставлять не у всех меток – метки на осях могут быть расположены в 2 или в 5 раз чаще, чем числа. Кроме опорных чисел и масштабных меток, никакие другие числа и метки у осей графика отмечать нельзя.
· Нанести на график экспериментальные точки в виде незакрашенных кружочков диаметром примерно 2 мм. Вокруг каждой из точек нанести два доверительных интервала – вертикальный и горизонтальный. Доверительный интервал можно не наносить только в том случае, если его геометрический размер меньше диаметра экспериментальной точки, то есть менее 2 мм. Рассчитывают доверительные интервалы обычно только для двух крайних точек графика, остальные интервалы наносят приблизительно – так, чтобы их размеры были промежуточными между размерами интервалов крайних точек.
· С помощью лекала проводят плавную линию так, чтобы она пересекла доверительные интервалы всех экспериментальных точек, сами точки не обязательно должны попасть на линию.






