Для того чтобы оценить приборную погрешность прямого измерения, достаточно знать класс точности g применяемого прибора, который указывается на шкале или корпусе прибора в виде одного из чисел: 0,01; 0,02; 0,1; 0,5; 1,0; 1,5; 2,5; 4,0. Смысл термина “класс точности” зависит от типа прибора. Отличить эти типы друг от друга можно по способу указания на них класса точности.
1 тип. Класс точности g указан на приборе в виде числа без каких-либо дополнительных значков. Например, прибор, шкала которого изображена на рис.2, обладает классом точности 1,5.
Шкала прибора с указанием класса точности
 |
Рис.2.
Приборы этого типа выполнены так, что их абсолютная приборная погрешность Dп(x) не зависит от результата измерения x, и поэтому относительная погрешность 
уменьшается с ростом x. При этом под классом точности понимается следующая величина:
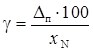, (4.1)
где x N – так называемое “ нормирующее значение”. Для всех приборов, которые применяются в учебной лаборатории, нормирующее значение – это предел измерения, то есть максимальное значение величины, которое может показать прибор. Например, у микроамперметра на рис.2 нормирующее значение x N = 100 мкА. Зная класс точности g и нормирующее значение x N, можно определить абсолютную приборную погрешность Dп(x) по формуле
. (4.2)
Относительная приборная погрешность, как указывалось выше, зависит от результата измерения x.
Микроамперметр, показанный на рис.2, обеспечивает абсолютную приборную погрешность измерения тока Dп(I) = 1,5×100/100 = 1,5 мкА, относительная приборная погрешность того результата, который показывает микроамперметр, то есть I = 36 мкА, составляет e п(I) = 1,5/36 = 0,04 = 4%.
2 тип. Класс точности g указан на приборе в виде числа, обведённого кружком. Пример такого прибора показан на рис.3. Приборы этого типа выполнены так, что их относительная приборная погрешность eп(x) не зависит от результата измерения x. Класс точности g в этих приборах – это относительная приборная погрешность eп(x), измеренная в процентах. Абсолютная приборная погрешность при этом зависит от результата измерения x – чем больше x, те больше Dп(x):
. (4.3)
Например, относительная погрешность измерения напряжения с помощью вольтметра, изображённого на рис.3, равна 2,5%, а абсолютная погрешность того результата, который показывает вольтметр, то есть U = 38 В, составляет Dп(U) = 2,5×38/100 = 1 В.
 |
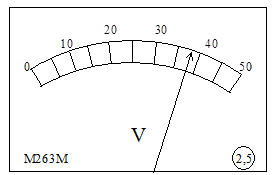Шкала прибора с указанием класса точности
Рис.3.
3 тип. Класс точности не указан. В этом случае, как и для приборов 1 типа, абсолютная погрешность Dп(x) не зависит от результата измерения x. Если прибор – цифровой, то Dп(x) равна 1 в младшем разряде прибора. Если прибор – не цифровой, например, миллиметровая линейка или штангенциркуль, то Dп(x) равна половине цены деления прибора.
