Условие (1) является достаточным для оптимальности расписания. То есть если для любой пары требований (i, j) из некоторого расписания условие (1) выполнено, то расписание оптимально. Однако строить оптимальное расписание с его помощью не слишком удобно, так как требуется большое количества проверок и переборов. Поэтому будет предложен алгоритм построения расписания, а затем будет доказано, что расписание, построенное с помощью этого алгоритма, удовлетворяет условию (1), то есть является оптимальным.
Алгоритм Джонсона
Шаг 1. В первую группу заносятся требования, у которых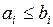 
; во вторую группу заносятся требования, у которых 
.
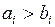Шаг 2. Требования из первой группы сортируются по неубыванию а i и в таком порядке занимают первые место в расписании.
Шаг 3. Требования из второй группы сортируются по невозрастанию b i и занимают в таком порядке последующие места в расписании.
Пример 2. Дано пять деталей, которые последовательно обрабатываются на двух станках. Время обработки каждой детали на каждом станке указано в таблице 5.
Таблица 5
| i | |||||
| a i | |||||
| b i |
В соответствии с требованиями алгоритма разобьем требования на группы:
Таблица 6
| I группа | II группа | ||||||
|
|
| ||||||
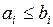
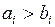
| i | i | ||||||
| a i | b i |
Оптимальное расписание 
. Длина расписания вычисляется в таблице 7.
Таблица 7
| σ | |||||
| f ia | |||||
| f ib |
Здесь общее время обслуживания равно 16.
Доказательство оптимальности алгоритма Джонсона
Докажем, что для расписания, полученного с помощью алгоритма Джонсона, выполнено условие (1).
В самом деле, пусть в расписании 
(i предшествует j). Тогда возможны три случая:
1. 
,
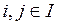2. 
,
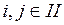3. 
.
(Возможен ли случай когд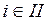а 
, а 
?)
Случай 1.
Если i и j принадлежат первой группе, то
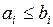, (8)
, (9)
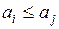, (10)
Тогда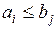 
, откуда следует, что 
.
Чтобы доказать, что (1) выполнено нужно показать, что 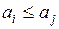и 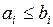. Но эти условия выполнены: (8), (10).
Упражнение 1. Докажите самостоятельно оптимальность алгоритма для второго случая. Подсказка: здесь будет выполнено 
.
Случай 3.
В этом случае имеем
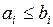, (11)
. (12)
Так как требования из первой и второй группы не связаны никакими зависимостями, то 
может достигаться как на 
так и на 
. Рассмотрим случай 3.1, где , то есть
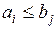(13)
и требуется доказать, что
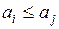(14)
и
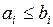(15)
(15) следует из (11). Далее из (12) и (13) следует 
, то есть выполняется (14).
Упражнение 2. Самостоятельно доказать для случая (12), где 
.
Замечание о сложности алгоритма. Поскольку алгоритм построения оптимального расписания состоит из сортировки, а сложность сортировки имеет порядок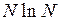 
, то можно сказать, что задача Джонсона с двумя приборами имеет полимиальную сложность.
Теория экономических информационных систем
