По способу отбора (способу формирования) выборки единиц из генеральной совокупности распространены следующие виды выборочного наблюдения:
* простая случайная выборка (собственно-случайная);
* типическая (стратифицированная);
* серийная (гнездовая);
* механическая;
* комбинированная;
* ступенчатая.
Простая случайная выборка (собственно-случайная) есть отбор единиц из генеральной совокупности путём случайного отбора, но при условии вероятности выбора любой единицы из генеральной совокупности. Отбор проводится методом жеребьёвки или по таблице случайных чисел.
Типическая (стратифицированная) выборка предполагает разделение неоднородной генеральной совокупности на типологические или районированные группы по какому-либо существенному признаку, после чего из каждой группы производится случайный отбор единиц.
Для серийной (гнездовой) выборки характерно то, что генеральная совокупность первоначально разбивается на определённые равновеликие или неравновеликие серии (единицы внутри серий связаны по определённому признаку), из которых путём случайного отбора отбираются серии и затем внутри отобранных серий проводится сплошное наблюдение.
Механическая выборка представляет собой отбор единиц через равные промежутки (по алфавиту, через временные промежутки, по пространственному способу и т.д.). При проведении механического отбора генеральная совокупность разбивается на равные по численности группы, из которых затем отбирается по одной единице.
Комбинированная выборка основана на сочетании нескольких способов выборки.
Многоступенчатая выборка есть образование внутри генеральной совокупности вначале крупных групп единиц, из которых образуются группы, меньшие по объёму, и так до тех пор, пока не будут отобраны те группы или отдельные единицы, которые необходимо исследовать.
Выборочный отбор может быть повторным и бесповторным. При повторном отборе вероятность выбора любой единицы не ограничена. При бесповторном отборе выбранная единица в исходную совокупность не возвращается.
Для отобранных единиц рассчитываются обобщённые показатели (средние или относительные) и в дальнейшем результаты выборочного исследования распространяются на всю генеральную совокупность.
При выборочном наблюдении решаются две задачи:
1) определение среднего размера изучаемого признака;
2) определение доли единиц, обладающих данным признаком.
Для определения средней ошибки выборки (р) применяются следующие формулы (табл. 3.1):
Таблица 3.1
Расчёт средней ошибки выборки
| Наименование показателей | Повторная выборка | Бесповторная выборка |
| Собственный случайный и механический отбор | ||
| а) при определении среднего размера изучаемого признака | 
| 
|
| б) при определении доли | 
| 
|
| Типический отбор | ||
| а) при определении среднего размера изучаемого признака | 
| 
|
| б) при определении доли данного признака | 
| 
|
| Серийный отбор | ||
| а) при определении среднего размера изучаемого признака | 
| 
|
| б) при определении доли |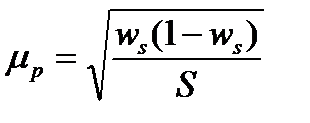 
| 
|
Предельная ошибка выборки (Δ) определяется по формулам:
, (3.14)
, (3.15)
где t - коэффициент доверия.
В статистических исследованиях с помощью формулы предельной ошибки можно решать ряд задач.
1. Определять возможные пределы нахождения характеристики генеральной совокупности на основе данных выборки.
Доверительные интервалы для генеральной средней можно установить на основе соотношений:
или 
, (3.16)
Доверительные интервалы для генеральной доли устанавливаются на основе соотношений:
или 
, (3.17)
2. Определять доверительную вероятность, которая означает, что характеристика генеральной совокупности отличается от выборочной на заданную величину.
Доверительная вероятность является функцией от t, где:
, (3.18)
Доверительная вероятность по величине t определяется по специальной таблице.
При обобщении результатов выборочного наблюдения наиболее часто используют следующие уровни вероятности и соответствующие им значения t:
| Р | 0,683 | 0,950 | 0,954 | 0,997 |
| t | 1,96 |
3. Определять необходимый объём выборки с помощью допустимой величины ошибки.
Определение необходимой численности выборки (n) производится на основе алгебраического преобразования формы предельных ошибок выборки.
1. При определении среднего размера признака
- повторный отбор, (3.19)
- бесповторный отбор (3.20)
2. При определении доли признака
- повторный отбор, (3.21)
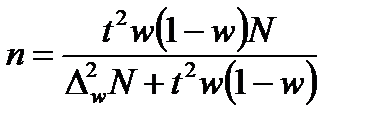- бесповторный отбор. (3.22)
