Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных. Потребность определения средних величин связана с тем, что у различных единиц исследуемых совокупностей индивидуальные значения одного и того же признака, как правило, неодинаковы.
Средней величиной называют показатель, который характеризует обобщённое значение признака или группы признаков в исследуемой совокупности.
Если исследуется совокупность с качественно однородными признаками, то средняя величина выступает здесь как типическая средняя. Например, для групп работников определённой отрасли с фиксированным уровнем дохода определяется типическая средняя расходов на предметы первой необходимости, т.е. типическая средняя обобщает качественно однородные значения признака в данной совокупности, каковым является доля расходов у работников данной группы на товары первой необходимости.
При исследовании совокупности с качественно разнородными признаками на первый план может выступить нетипичность средних показателей. Такими, к примеру, являются средние показатели произведённого национального дохода на душу населения (разные возрастные группы), средние показатели урожайности зерновых культур по всей территории России (районы разных климатических зон и разных зерновых культур), средние показатели рождаемости населения по всем регионам страны, средние температуры за определенный период и т.д. Здесь средние величины обобщают качественно разнородные значения признаков или системных пространственных совокупностей (международное сообщество, континент, государство, регион, район и т.д.) или динамических совокупностей, протяженных во времени (век, десятилетие, год, сезон и т.д.). Такие средние величины называют системными средними.
Таким образом, значение средних величин состоит в их обобщающей функции. Средняя величина заменяет большое число индивидуальных значений признака, обнаруживая общие свойства, присущие всем единицам совокупности. Это, в свою очередь, позволяет избежать случайных причин и выявить общие закономерности, обусловленные общими причинами.
2. Виды средних величин и методы их расчёта
На этапе статистической обработки могут быть поставлены самые различные задачи исследования, для решения которых нужно выбрать соответствующую среднюю. При этом необходимо руководствоваться следующим правилом: величины, которые представляют собой числитель и знаменатель средней, должны быть логически связаны между собой.
Используются две категории средних величин (рис. 2.14):
* степенные средние;
* структурные средние.
Первая категория степенных средних включает: среднюю арифметическую, среднюю гармоническую, среднюю квадратическую, среднюю геометрическую и средняя кубическая.
Рис. 2.14. Виды средних в статистике
Вторая категория (структурные средние) - это мода и медиана. Эти виды средних будут рассмотрены в теме: «Структурные характеристики вариационного ряда распределения».
Введём следующие условные обозначения:
- средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;
- варианты (значение) осредняемого признака или серединное значение интервала, в котором измеряется вариант;
n – число вариант;
- частота (повторяемость индивидуальных значений признака).
k - показатель степени.
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.
Простая средняя считается по не сгруппированным данным и имеет следующий вид:
, (2.15)
Взвешенная средняя считается по сгруппированным данным и имеет общий вид:
. (2.16)
В зависимости от того, какое значение принимает показатель степени, различают следующие виды степенных средних:
- средняя арифметическая, если k = 1;
- средняя гармоническая, если k = -1;
- средняя геометрическая, если k = 0;
- средняя квадратическая, если k = 2;
- средняя кубическая, если k = 3.
Формулы степенных средних приведены в табл. 2.9.
Таблица 2.9
Виды степенных средних
| Вид степенной средней | Показатель степени ( )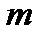
| Формула расчета | |
| простая | взвешенная | ||
| гармоническая | - 1 | 
| 
|
| геометрическая | 
| 
| |
| арифметическая | 
| 
| |
| квадратическая | 
| 
| |
| кубическая |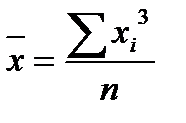 
| 
|
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени k увеличивается и соответствующая средняя величина:
, (2.17)
В статистической практике чаще, чем остальные виды средних взвешенных, используется средняя арифметическая и средняя гармоническая взвешенные. Выбор вида степенной средней определяется экономическим содержанием задачи и наличием данных.
Рассмотрим среднюю арифметическую простую и взвешенную.
Пример: Студент Петров по результатам учебного семестра имеет следующие оценки: теория бухгалтерского учета - 4, экономическая статистика - 5, финансы, денежное обращение и кредит - 3, экономика фирмы - 2. Какова его средняя оценка по результатам семестра?
Поскольку каждая оценка встречается один раз, для расчета средней применяем формулу арифметической простой:
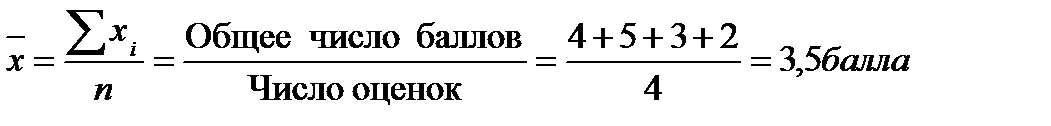
Перечисленные дисциплины студент Петров сдал в среднем на 3,5 балла.
Пример: Имеются следующие данные о распределении бригад по уровню выработки продукции (табл. 2.10).
Таблица 2.10
