Пример 1
По семи территориям Уральского района за 199Х г. известны значения двух признаков.
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская респ. | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55,0 | 58,8 |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
Требуется:
1. Для характеристики зависимости у и х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы.
2. Оценить каждую модель через среднюю ошибку аппроксимации 
и F – критерий Фишера, коэффициент корреляции.
Решение. 1а. Для расчета параметров a и b линейной регрессии y=a+bx решаем систему нормальных уравнений относительно a и b:
По исходным данным рассчитываем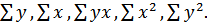 
| y | x | yx | x2 | y2 | 
| 
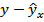
| Ai | |
| 68,8 | 45,1 | 3102,88 | 2034,01 | 4733,44 | 61,3 | 7,5 | 10,9 | |
| 61,2 | 59,0 | 3610,80 | 3481,00 | 3745,44 | 56,5 | 4,7 | 7,7 | |
| 59,9 | 57,2 | 3426,28 | 3271,84 | 3588,01 | 57,1 | 2,8 | 4,7 | |
| 56,7 | 61,8 | 3504,06 | 3819,24 | 3214,89 | 55,5 | 1,2 | 2,1 | |
| 55,0 | 58,8 | 3234,00 | 3457,44 | 3025,00 | 56,5 | -1,5 | 2,7 | |
| 54,3 | 47,2 | 2562,96 | 2227,84 | 2948,49 | 60,5 | -6,2 | 11,4 | |
| 49,3 | 55,2 | 2721,36 | 3047,04 | 2430,49 | 57,8 | -8,5 | 17,2 | |
| Итого | 405,2 | 384,3 | 22162,34 | 21338,41 | 23685,76 | 405,2 | 0,0 | 56,7 |
| Ср. Знач. | 57,89 | 54,90 | 3166,05 | 3048,34 | 3383,68 | x | x | 8,1 |
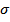
| 5,74 | 5,86 | x | x | x | x | x | x |
| 32,92 | 34,34 | x | x | x | x | x | x |
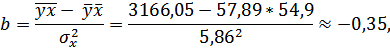
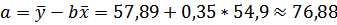
Уравнение регрессии: 
. С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %.
Рассчитаем линейный коэффициент парной корреляции:
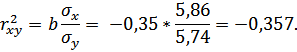
Связь умеренная, обратная.
Определим коэффициент детерминации:
Вариация результата на 12,7 % объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения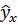 
.Найдем величину средней ошибки аппроксимации :
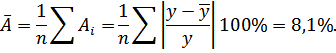
В среднем расчетные данные отклоняются от фактических на 8,1 %.
Рассчитаем F – критерий:
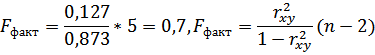
поскольку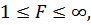 
следует рассмотреть F -1.
Полученное значение указывает на необходимость принять гипотезу Н0 о случайной природе выявленной зависимости и статистической значимости параметров уравнения и показателя тесноты связи.
1б. Построению степенной модели y=axb предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
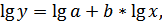
где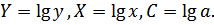 
Для расчетов используем данные.
| Y | X | YX | Y2 | X2 |
|
| 
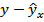
| Ai | |
| 1,8376 | 1,6542 | 3,0398 | 3,3768 | 2,7364 | 61,0 | 7,8 | 60,8 | 11,3 | |
| 1,7868 | 1,7709 | 3,1642 | 3,1927 | 3,1361 | 56,3 | 4,9 | 24,0 | 8,0 | |
| 1,7774 | 1,7574 | 3,1236 | 3,1592 | 3,0885 | 56,8 | 3,1 | 9,6 | 5,2 | |
| 1,7536 | 1,7910 | 3,1407 | 3,0751 | 3,2077 | 55,5 | 1,2 | 1,4 | 2,1 | |
| 1,7404 | 1,7694 | 3,0795 | 3,0290 | 3,1308 | 56,3 | -1,3 | 1,7 | 2,4 | |
| 1,7348 | 1,6739 | 2,9039 | 3,0095 | 2,8019 | 60,2 | -5,9 | 34,8 | 10,9 | |
| 1,6928 | 1,7419 | 2,9487 | 2,8656 | 3,0342 | 57,4 | -8,1 | 65,6 | 16,4 | |
| Итого | 12,3234 | 12,1587 | 21,4003 | 21,7078 | 21,1355 | 403,5 | 1,7 | 197,9 | 56,3 |
| Ср.знач | 1,7605 | 1,7370 | 3,0572 | 3,1011 | 3,0194 | x | x | 28,27 | 8,0 |
|
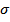
| 0,0425 | 0,0484 | x | x | x | x | x | x | x |
|
| 0,0018 | 0,0023 | x | x | x | x | x | x | x |
Рассчитаем C и b:
Получим линейное уравнение: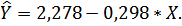 
Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата ух. По ним рассчитаем показатели: тесноты связи – индекс корреляции р ху и среднюю ошибку аппроксимации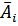 
:
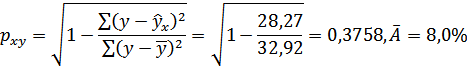
Характеристики степенной модели указывают, что она несколько лучше линейной функции описывает взаимосвязь.
1в. Построению уравнения показательной кривой y=abx предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:
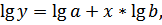
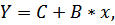
где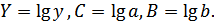 
Для расчетов используем таблицы:
| Y | x | Yx | Y2 | X2 | yх | y- yх | (y- yх)2 | Ai | |
| 1,8376 | 45,1 | 82,8758 | 3,3768 | 2034,01 | 60,7 | 7,0 | 49,00 | 10,2 | |
| 1,7868 | 59,0 | 105,4212 | 3,1927 | 3481,00 | 56,4 | 4,9 | 24,01 | 8,0 | |
| 1,7774 | 57,2 | 101,6673 | 3,1592 | 3271,84 | 56,9 | 3,0 | 9,00 | 5,0 | |
| 1,7536 | 61,8 | 108,3725 | 3,0751 | 3819,24 | 55,5 | 1,2 | 1,44 | 2,1 | |
| 1,7404 | 58,8 | 102,3355 | 3,0290 | 3457,44 | 56,4 | -1,4 | 1,96 | 2,5 | |
| 1,7348 | 47,2 | 81,8826 | 3,0095 | 2227,84 | 60,0 | -6,5 | 42,25 | 12,0 | |
| 1,6928 | 55,2 | 93,4426 | 2,8656 | 3047,04 | 57,5 | -8,2 | 67,24 | 16,6 | |
| Итого | 12,3234 | 384,3 | 675,9974 | 21,7078 | 21338,41 | 403,4 | 0,0 | 194,90 | 56,2 |
| Ср.знач | 1,7605 | 54,9 | 96,5711 | 3,1011 | 3048,34 | x | x | 27,84 | 8,1 |
|
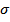
| 0,0425 | 5,86 | x | x | x | x | x | x | x |
|
| 0,0018 | 34,3396 | x | x | x | x | x | x | x |
Значения параметров регрессии A и B составили:
Получено линейное уравнение: 
.
Произведем потенцирование полученного уравнения и запишем его в обычной форме:
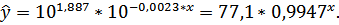
Тесноту связи оценим через индекс корреляции рху:
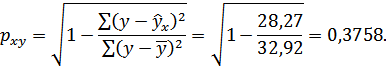
Связь умеренная.
что говорит о повышенной ошибке аппроксимации, но в допустимых пределах. Показательная функция чуть хуже, чем степенная, описывает изучаемую зависимость.
1г. Уравнение равносторонней гиперболы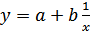 
линеаризируется при замене: 
Тогда 
Для расчетов используем данные таблицы:
| y | z | yz | z2 | y2 | yх | y- yх | (y- yх)2 | Ai | |
| 68,8 | 0,0222 | 1,5255 | 0,000492 | 4733,44 | 61,8 | 7,0 | 49,00 | 10,2 | |
| 61,2 | 0,0169 | 1,0373 | 0,000287 | 3745,44 | 56,3 | 4,9 | 24,01 | 8,0 | |
| 59,9 | 0,0175 | 1,0472 | 0,000306 | 3588,01 | 56,9 | 3,0 | 9,00 | 5,0 | |
| 56,7 | 0,0162 | 0,9175 | 0,000262 | 3214,89 | 55,5 | 1,2 | 1,44 | 2,1 | |
| 0,0170 | 0,9354 | 0,000289 | 3025,00 | 56,4 | -1,4 | 1,96 | 2,5 | ||
| 54,3 | 0,0212 | 1,1504 | 0,000449 | 2948,49 | 60,8 | -6,5 | 42,25 | 12,0 | |
| 49,3 | 0,0181 | 0,8931 | 0,000328 | 2430,49 | 57,5 | -8,2 | 67,24 | 16,6 | |
| Итого | 405,2 | 0,1291 | 7,5064 | 0,002413 | 23685,76 | 405,2 | 0,0 | 194,90 | 56,5 |
| Ср.знач | 57,9 | 0,0184 | 1,0723 | 0,000345 | 3383,68 | x | x | 27,84 | 8,1 |
|
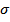
| 5,74 | 0,002145 | x | x | x | x | x | x | x |
|
| 32,9476 | 0,000005 | x | x | x | x | x | x | x |
Значения параметров регрессии a и b составили:
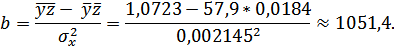
Получено уравнение: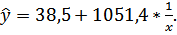 
Индекс корреляции: 
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи: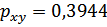 
(по сравнению с линейной, степенной и показательной регрессиями). остается на допустимом уровне, расчетное значение критерия Фишера равно:
где 
Следовательно, принимается гипотеза Н0 о статистически незначимых параметрах этого уравнения. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений.
Анализ полученных уравнений:
| № п/п | Видуравнения | Коэффициент корреляции | Ошибка аппроксимации | Критерий Фишера Fфакт | Выбор |
Линейное уравнение
| -0,357 | 8,1% | 0,7 при a =0,05 | ||
Степенная модель
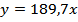
| Индекс корреляции -0,298 | 8,0% | 0,76 | ||
Показательное уравнение
| Индекс корреляции 0,3589 | 8,0% | 0,8 | выбрано | |
Уравнение равносторонней гиперболы
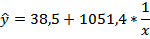
| Индекс корреляции 0,3944 | 8,1% | 0,92 при a =0,05 |
Задание
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи
2. Рассчитайте параметры 3 уравнений из следующих типов уравнений: линейное, степенное, экспоненциальное, полулогарифмическое, обратное, гиперболическое.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Оцените с помощью средней ошибки аппроксимации качество уравнений.
5. Оцените с помощью F— критерия Фишера статистическую надежность результатов регрессионного моделирования.
6. Сделайте оценку силы связи фактора с результатом с помощью среднего (общего) коэффициента эластичности.
7. Сведите результаты расчета в общую таблицу и сделайте выводы о выборе уравнения.
Вариант 1.
Изучается зависимость материалоемкости продукции от размера предприятия по 10 однородным заводам.
| Показатель | Материалоемкость продукции по заводам | |||||||||
| Потреблено материалов на единицу продукции, кг. У | 3,7 | 3,6 | 3,5 | 3,5 | ||||||
| Выпуск продукции, тыс. ед. Х |
Вариант 2.
По территориям Центрального района известны данные 2005г.
| Район | Доля денежных доходов, направленных на прирост сбережений во вкладах, займах, сертификатах и на покупку валюты, в общей сумме среднедушевого денежного дохода, %, у | Среднемесячная начисленная заработная плата, тыс.руб., х |
| Брянская обл. | 6,9 | |
| Владимирская обл. | 8,7 | |
| Ивановская обл. | 6,4 | |
| Калужская обл. | 8,4 | |
| Костромская обл. | 6,1 | |
| Орловская обл. | 9,4 | |
| Рязанская обл. | 11,0 | |
| Смоленская обл. | 6,4 | |
| Тверская обл. | 9,3 | |
| Тульская обл. | 8,2 | |
| Ярославская обл. | 8,6 |
Вариант 3.
По территориям Центрального района известны данные 1995г.
| Район | Средний размер назначенных ежемесячных пенсий, тыс.руб., у | Прожиточный минимум в среднем на одного пенсионера в месяц, тыс.руб., х |
| Брянская обл. | ||
| Владимирская обл. | ||
| Ивановская обл. | ||
| Калужская обл. |
Продолжение
| Костромская обл. | ||
| г. Москва | ||
| Московская обл. | ||
| Орловская обл. | ||
| Рязанская обл. | ||
| Смоленская обл. | ||
| Тверская обл. | ||
| Тульская обл. | ||
| Ярославская обл. |
Вариант 4
По территориям Центрального и Волго–Вятского районов известны данные за ноябрь 1997г.
| Район | Средняя заработная плата и выплаты социального характера, тыс.руб., у | Прожиточный минимум в среднем на душу населения, тыс.руб., х |
| Центральный | ||
| Брянская обл. | ||
| Владимирская обл. | ||
| Ивановская обл. | ||
| Калужская обл. | ||
| Костромская обл. | ||
| Орловская обл. | ||
| Рязанская обл. | ||
| Смоленская обл. | ||
| Тверская обл. | ||
| Тульская обл. | ||
| Ярославская обл. | ||
| Волго-Вятский | ||
| Респ. Марий Эл | ||
| Респ. Мордовия | ||
| Чувашская Респ. | ||
| Кировская обл. | ||
| Нижегородская обл. |
Вариант 5
По территориям Волго–Вятского, Центрально–Черноземного и Поволжского районов известны данные за ноябрь 1997г.
| Район | Потребительские расходы в расчете на душу населения, тыс.руб., у | Средняя заработная плата и выплаты социального характера, тыс.руб., х |
| Волго-Вятский | ||
| Респ. Марий Эл | ||
| Респ. Мордовия | ||
| Чувашская Респ. | ||
| Кировская обл. | ||
| Нижегородская обл. | ||
| Центрально-Черноземный | ||
| Белгородская обл. | ||
| Воронежская обл. | ||
| Курская обл. | ||
| Липецкая обл. | ||
| Тамбовская обл. | ||
| Поволжский | ||
| Респ. Калмыкия | ||
| Респ. Татарстан | ||
| Астраханская обл. | ||
| Волгоградская обл. | ||
| Пензенская обл. | ||
| Саратовская обл. | ||
| Ульяновская обл. |
Вариант 6
По территориям Северного, Северо–Западного и Центрального районов известны данные за ноябрь 1997г.
| Район | Потребительские расходы на душу населения, тыс.руб., у | Денежные доходы на душу населения, тыс.руб., х | ||
| Северный | ||||
| Респ. Карелия | ||||
| Респ. Коми | ||||
| Архангельская обл. | ||||
| Вологодская обл. | ||||
| Мурманская обл. | ||||
| Северо-Западный | ||||
| Ленинградская обл. | ||||
| Новгородская обл. | ||||
| Псковская обл. | ||||
| Центральный | ||||
| Брянская обл. | ||||
| Владимирская обл. | ||||
| Ивановская обл. | ||||
| Калужская обл. | ||||
| Костромская обл. | ||||
| Московская обл. | ||||
| Орловская обл. | ||||
| Рязанская обл. | ||||
| Смоленская обл. | ||||
| Тверская обл. | ||||
| Тульская обл. | ||||
| Ярославская обл. | ||||
Вариант 7
По территориям Восточно–Сибирского и Дальневосточного районов известны данные за ноябрь 1997г.
| Район | Потребительские расходы на душу населения, тыс.руб., у | Денежные доходы на душу населения, тыс.руб., х |
| Восточно-Сибирский | ||
| Респ. Бурятия | ||
| Респ. Тыва | ||
| Респ. Хакасия | ||
| Красноярский край | ||
| Иркутская обл. | ||
| Усть–Ордынский Бурятский авт.округ | ||
| Читинская обл. | ||
| Дальневосточный | ||
| Респ. Саха (Якутия) | ||
| Еврейский авт. Округ | ||
| Чукотский авт. Округ | ||
| Приморский край | ||
| Хабаровский край | ||
| Амурская обл. | ||
| Камчатская обл. | ||
| Магаданская обл. | ||
| Сахалинская обл. |
Вариант 8
По территориям Уральского и Западно–Сибирского районов известны данные за ноябрь 1997г.
| Район | Потребительские расходы на душу населения, тыс.руб., у | Денежные доходы на душу населения, тыс.руб., х |
| Уральский | ||
| Респ. Башкортостан | ||
| УдмуртскаяРесп. | ||
| Курганская обл. | ||
| Оренбургская обл. | ||
| Пермская обл. | ||
| Свердловская обл. | ||
| Челябинская обл. | ||
| Западно–Сибирский | ||
| Респ. Алтай | ||
| Алтайский край | ||
| Кемеровская обл. | ||
| Новосибирская обл. | ||
| Омская обл. | ||
| Томская обл. | ||
| Тюменская обл. |
Вариант 9
По территориям Уральского и Западно–Сибирского районов известные данные за ноябрь 1997г.
| Район | Потребительские расходы на душу населения, тыс.руб., у | Денежные доходы на душу населения, тыс.руб., х |
| Уральский | ||
| Республика Башкортостан | ||
| Удмуртская Респ. | ||
| Курганская обл. | ||
| Оренбургская обл. | ||
| Пермская обл. | ||
| Свердловская обл. | ||
| Челябинская обл. | ||
| Западно–Сибирский район | ||
| Респ. Алтай | ||
| Алтайский край | ||
| Кемеровская обл. | ||
| Новосибирская обл. | ||
| Омская обл. | ||
| Томская обл. | ||
| Тюменская обл. |
Вариант 10
Имеются данные по странам за 1994г.
| Страна | Душевой доход, долл., у | Индекс человеческого развития (ИЧР), x1 | Индекс челове-ческой бедности (ИЧБ), x2 | |||
| Объединенные Арабские Эмираты | 0,866 | 14,9 | ||||
| Таиланд | 0,833 | 11,7 | ||||
| Уругвай | 0,883 | 11,7 | ||||
| Ливия | 0,801 | 18,8 | ||||
| Колумбия | 0,848 | 10,7 | ||||
| Иордания | 0,730 | 10,9 | ||||
| Египет | 0,514 | 34,8 | ||||
| Марокко | 0,566 | 41,7 | ||||
| Перу | 0,717 | 22,8 | ||||
| Шри-Ланка | 0,711 | 20,7 | ||||
| Филиппины | 0,672 | 17,7 | ||||
| Боливия | 0,589 | 22,5 | ||||
| Китай | 0,626 | 17,5 | ||||
| Зимбабве | 0,513 | 17,3 | ||||
| Пакистан | 0,445 | 46,8 | ||||
| Уганда | 0,328 | 41,3 | ||||
| Нигерия | 0,393 | 41,6 | ||||
| Индия | 0,446 | 36,7 | ||||
Рекомендации по организации выполнения самостоятельной работы, примерный календарный план выполнения
Самостоятельная работа состоит из трех разделов: теория вероятности, математическая статистика и регрессионный анализ.
Первая часть - решение задач по теории вероятности должны выполняться в течение первых 5 недель по мере чтения лекционного материала и тематики практических занятий. При оформлении работы обязательны:
–текст задачи;
–приведение теоретического материала, используемого при решении со ссылкой на литературные источники;
–численное решение, четкий ответ.
Вторая часть - математическая статистика. Выполняется в течение следующей трети семестра, в основном на практических занятиях, с использованием компьютера для расчета и оформления таблиц и графиков.
Третья часть - регрессионный анализ. Работа должна содержать введение, где формулируется цель работы. Включает теоретическую часть описания метода наименьших квадратов, выбор не менее трех видов предполагаемых уравнений (линейная, степенная и т. д.). Для выбора типа уравнения используется рисунок поля исходных данных, с подбором нужного масштаба, с тем, чтобы можно было предположить вид уравнения.
В конце работы должна быть составлена сводная таблица с указанием вида уравнения, с числовыми параметрами, коэффициент корреляции, ошибка аппроксимации, критерий Фишера или Стьюдента табличный и для каждого уравнения и сделан вывод, какое уравнение рекомендуется к использованию.
Защита проходит в форме собеседования по темам
Рекомендуемая литература
Основная литература:
1. Письменный, Д. Т.Конспект лекций по теории вероятностей, математической статистике и случайным процессам/ Д. Т. Письменный. - 4-е изд., испр. - М.: Айрис-пресс, 2008. – 288 с. – (Высшее образование).
2. Рябушко, А. П. Индивидуальные задания по высшей математике: в 4 ч.: учеб. пособие / А. П. Рябушко, Ч. 4, Операционное исчисление. Элементы теории устойчивости. Теория вероятностей. Математическая статистика. - 2-е изд., испр. - Мн.: Вышэйш. шк., 2007.
Дополнительная литература:
1. Гмурман, В. Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В. Е. Гмурман. - Изд. 10-е, стер. - М.: Высшая школа, 2004. - 479 с. - Прил.: с. 461-473. - Пред. указ.: с. 474-479. - ISBN 5-06-004214-6
2. Королев, В. Ю. Теория вероятностей и математическая статистика: учебник / В. Ю. Королев; МГУ им. М. В. Ломоносова, фак. вычислит. матем. и кибернетики. - М.: Проспект, 2006. - 160 с. - Библиогр.: с. 160. - ISBN 5-482-00274-8
3. Вентцель, Е. С. Теория вероятностей и ее инженерные приложения: учеб. пособие для вузов / Е. С. Вентцель, Л. А. Овчаров. - 2-е изд., стер. - М.: Высшая школа, 2000. - 480 с.: ил. - Библиогр. с. 477. - ISBN 5-06-003830-0
4. Кремер, Н. Ш. Теория вероятностей и математическая статистика: учеб. пособие для вузов / Н. Ш. Кремер. - М.: ЮНИТИ, 2000. - 543 с.: ил. - Библиогр.: с. 509-510. - Прил.: с. 526-534. - Предм. указ.: с. 535-543. - ISBN 5-238-00141-Х
Методическая литература.
Методические указания к выполнению контрольной работы по дисциплине "Теория вероятности и математическая статистика" для студентов специальности 090105.65 Комплексное обеспечение информационной безопасности / сост. М.А. Мартынова; рец. А.С. Адамчук</font>. - Ставрополь: СевКавГТУ, 2009. - 75 с.: ил.
