Суммой А+В событий А и В называется событие, состоящее в том, что в результате опыта наступит или событие А, или событие В, или оба вместе. (Другими словами суммой А+В событий А и В называется событие, состоящее в появлении хотя бы одного из этих событий).
Если события А и В несовместны, то А+В – это или событие А, или событие В.
Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Произведением АВ событий А и В называется событие, состоящее в совместном появлении и события А и события В.
Произведением нескольких событий называется событие, состоящее в их совместном появлении.
Событием, противоположным событию А, называется событие, обозначаемое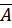 
и состоящее в том, что в результате опыта событие А не наступит.
Теорема сложения вероятностей несовместимых событий:
Вероятность суммы двух несовместимых событий равна сумме вероятностей
этих событий:
.
Следствие 1. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Следствие 2. Если события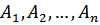 
образуют полную группу событий, то сумма их вероятностей равна единице:
Следствие 3. Сумма вероятностей противоположных событий равна единице: 
Пример 2
В ящике 4 белых, 5 красных и 6 зеленых шаров. Шары перемешивают и наудачу извлекают один шар. Какова вероятность события, состоящего в том, что шар окажется цветным?
Решение
Обозначим:
А - событие, состоящее в том, что извлеченный шар окажется красным,
В - событие, состоящее в том, что извлеченный шар окажется зеленым.
Интересующее нас событие состоит в появлении события A+B. Так как
А и В несовместны, то 
Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любой совокупности остальных.
Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Вероятность события А, вычисляемая при условии, что событие В произошло, называется условной вероятностью события А и обозначается PB(A).
Теорема умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое из них произошло:
Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А,
Следствие 2. Вероятность произведения двух независимых событий раина произведению вероятностей этих событий:
Для вычисления вероятности совместного появления большего числа событий, например, четырех, используют формулу:
Для нескольких независимых в совокупности событий вероятность их произведения равна произведению их вероятностей:
Следствие 3. Вероятность появления хотя бы одного из событий 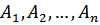, независимых в совокупности, равна разности единицы и произведения вероятностей противоположных событий 
.
Пример 3
В ящике 4 белых и 6 черных шаров. После перемешивания наудачу извлекаются два шара. Какова вероятность того, что оба извлеченных шара – белые?
Решение
A - событие, заключающееся в том, что 1-й извлеченный шар белый.
В - событие, заключающееся в том, что 2-й извлеченный шар белый.
Тогда АВ - событие, заключающееся в том, что оба извлеченные шара белые:
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.
Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Пример 4
Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор равно 0, 92, второй - 0, 95. Найти вероятность того, что при аварии сработает хотя бы один сигнализатор.
Решение
Обозначим: А - сработает 1-й сигнализатор, В – сработает 2-й сигнализатор. По условию Р(А)=0, 92, Р(В)=0, 95. А+В – срабатывает хотя бы один сигнализатор:
