Статистической называется гипотеза о неизвестном законе распределения случайной величины или о параметрах закона распределения, вид которого известен.
Пусть имеется статистическое распределение выборки для случайной величины X:
| xi | x1 | x2 | x3 | … | xk |
| ni | n1 | n2 | n3 | … | nk |
По виду полигона пли гистограммы, сравниваяих с графиками дифференциальных функций распределения, делаем предположение о виде закона распределения случайной величины. Сделанное предположение (гипотеза) подтверждается расчетами критерия согласия. Имеются различные критерии согласия: Хинчина, Колмогорова, Пирсона и др. Например, критерий Пирсона (хи-квадрат)
позволяет сравнивать близость частот ni данного статистического распределения выборки с теоретическими частотами n i¢, найденными с помощью функции распределения предполагаемого закона по формулам:
Здесь f(x) – дифференциальная, F(x) – интегральная функции предполагаемого распределения.
Если вычисленное значение критерия c2 - не превосходит некоторого критического значенияc2кр, взятого по таблице (приложение 3), то выдвинутая гипотеза принимается с заданным уровнем надежности (вероятности) g=1 - a. В противном случае гипотеза отвергается. В таблице:
a – уровень значимости, это вероятность отвергнуть правильную гипотезу;
S – число степеней свободы,S = k – 1 – r, где r – число параметров предполагаемого распределения; r = 2 для нормального распределения (а и s), г = 1 для показательного распределения (l).
Решение типового варианта
Исходной информацией будет Вариант 0 ( 
), данный ниже в п. 1.2.8.
По выборке построим интервальный вариационный ряд. Просмотрев все исходные данные, найдем 
Размах 
Интервал вариационного ряда равен 
. Начало первого интервала равно 
Таблица 1
| Интервалы | Рабочее поле | ni, частота | ni/n, частость | Накопление частости |
| 59-61 | 0,005 | 0,005 | ||
| 61-63 | 0,010 | 0,015 | ||
| 63-65 | 0,035 | 0,050 | ||
| 65-67 | 0,080 | 0,130 | ||
| 67-69 | 0,135 | 0,265 | ||
| 69-71 | 0,200 | 0,465 | ||
| 71-73 | 0,190 | 0,655 | ||
| 73-75 | 0,190 | 0,845 | ||
| 75-77 | 0,090 | 0,935 | ||
| 77-79 | 0,045 | 0,980 | ||
| 79-81 | 0,015 | 0,995 | ||
| 81-83 | 0,005 | 1,00 | ||
| ∑ | 1,000 | - |
Для построения графиков полигона и гистограммы мы можем использовать данные частоты 
или частости (относительные частоты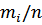 
). Изображаем на оси х значения интервалов на оси у частости 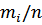и получаем (рис.2) и (рис.3). Эмпирическую функцию распределения 
находим, используя формулу 
и накопленные частости из таблицы 1. Учитываем, что в качестве представителя (x) каждого интервала взят его конец. Принимая за координаты точек концы интервалов и соответствующие накопленные частости (табл. 1) и соединяя эти точки, построим график эмпирической функции распределения (рис. 4).
Рис. 2. Полигон вариационного ряда выборки
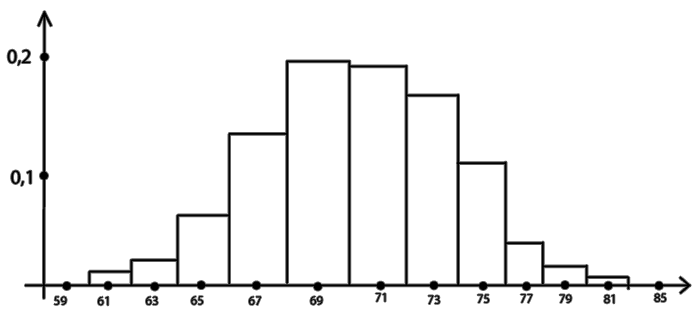
Рис. 3. Гистограмма вариационного ряда выборки
Рис. 4. График эмпирической функции распределения выборки
