Данный раздел методических указаний предполагает приобретение студентами опыта построения на экспериментальных данных моделей, выбора метода оценки параметров модели, получение прогнозных оценок.
Парная регрессия – уравнение связи двух переменных у и х:
,
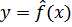где у – зависимая переменная (результативный признак);
х – независимая, объясняющая переменная (признак–фактор).
Различают линейные и нелинейные регрессии.
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
– полиномы различных степеней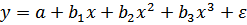 
;
– равносторонняя гипербола 
Регрессии, нелинейные по оцениваемым параметрам:
– степенная 
;
– показательная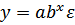 
;
– экспоненциальная 
.
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессии, линейные по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака y от теоретических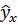 
минимальна, т.е.
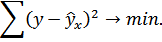
Для линейных и нелинейных уравнений, проводимых к линейным, решается система относительно а и b:
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
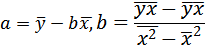
Тесноту связи изучаемых явлений оценивает линейные коэффициенты парной корреляции rxy для линейной регрессии 
:
и индекс корреляции рху – для нелинейной регрессии 
:
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
Допустимый предел значений 
– не более 8 – 10%.
Средний коэффициент эластичности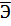 
показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1%:
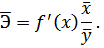
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R2:
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
F – текст – оценивание качества уравнения регрессии – состоит в проверке гипотезы Н0 о статической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F – критерия Фишера. Fфакт определяется по формуле:
где n – число единиц совокупности;
m – число параметров при переменных х;
к – число параметров в уравнении.
Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a –вероятность отвергнуть правильную гипотезу при условии, что она верна.
Обычно a принимается равной 0,05 или 0,01.
Если Fтабл < Fфакт, то Н0 – гипотеза о случайно природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если Fтабл > Fфакт, то гипотеза Н0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.