Задача 9. (8.16 [1]) Найти косинус угла между векторами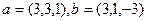 
.
Решение. Известно, что 
.
, 
.
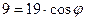, тогда 
, что приблизительно равно 0,5, то есть угол чуть больше 600.
Ответ. cos = 9/19.
Задача 10. Найти скалярное и векторное произведение векторов:
и 
.
Решение.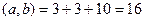 
.
Для поиска векторого произведения запишем определитель.
= 
= 
.
Ответ. Скалярное: 16, векторное: (-13, -1, -8).
Задача 11. Дано: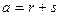 
, 
, 
, 
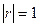, угол между векторами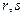 
45 градусов. Найти 
.
Решение.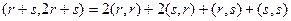 
= 
= 
.
Примечание. Как видим, можно вычислять скалярное произведение, даже не зная коорднат векторов. Здесь фактически 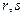служат в качестве базисных векторов, и через них выражены 
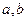, то есть (1,1) и (2,1) координаты 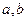относительно базиса .
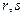Ответ. .
Практика № 6 (23 сентября у обеих групп).
45 минут - продолжение темы «скалярное, векторное, смешанное проиведение». Повторение перед контрольной.
Задачи 1,2,3.
Векторы a,b выражены через p,r: 
, 
. 
, угол между ними 45 град.
Задача 1. Найти . Задача 2. Найти | [a,b] |.
Задача 3. Найти 
Решение задачи 1.
= 
= 
.
Это мы раскрыли скобки, используя свойства скалярного произведения. Далее, так как 
то объединим их, и получим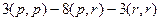 
.
Это можно выразить так:
и получаем 
. Ответ. 29.
Решение задачи 2.
= 
= 
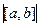Несмотря на то, что скобки мы раскрыли похожим образом, дальше будет существенное отличие, т.к. свойства векторного произведения совсем другие, чем скалярного. Так,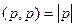 
, но 
. Кроме того, чтобы объединить 
в одно слагаемое, здесь надо сначала у одной из них сменить знак.
= 
=
= 
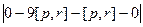. Модуль векторного произведения 
и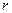 
это площадь параллелограмма, где эти векторы являются сторонами, поэтому далее можно продолжить так:
= 
= 
= 50. Ответ. 50.
Решение задачи 3.
= 
= 
= 
=
= 
=
= 
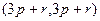= 257. Ответ. 257.
Задача 4. (8.19 [1]) Вычислить площадь параллелограмма, образованного векторами 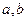, если 
, 
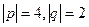, угол между p,q равен 
.
Решение. Вычислим площадь с помощью векторного произведения. =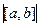 
= 
=
= 
= 
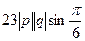= 92. Ответ 92.
Задача 5. Вывод формулы проекции вектора на ось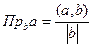 
.
Во-первых,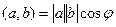 
.
(чертёж с доски)
Во-вторых, длина проекции 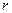это катет, 
гипотенуза треугольника, поэтому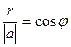 
. Получается, что 
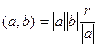, то есть 
, откуда и следует 
.
Задача 6. (8.18 [1]) Найти проекцию вектора 
на ось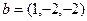 
.
Решение. =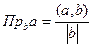 
= 
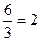. Ответ. 2.
Задача 7. Найти смешанное произведение трёх векторов:
.
Решение. Вычислим определитель:
= 
= 
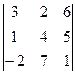. Ответ. .
Домашнее задание. Векторы a,b выражены через p,q: 
, 
. 
, угол между ними 600.
№ 1. Найти . № 2. Найти | [a,b] |.
45 минут - контрольная работа. Темы:
1. Умножение матриц
2. Определитель (3-го порядка).
3. Обратная матрица (3-го порядка).
4. Ранг матрицы.
Практика № 7
Подробный разбор домашних задач по скалярному и векторному произведению).
Задача 1. Векторы a,b выражены через p,q: , . , угол между ними 600. Найти .
Решение. = 
= 
= 
=
= 
=
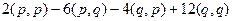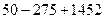= 1227.
Ответ. 1227.
Задача 2. Векторы a,b выражены через p,q: , . , угол между ними 600. Найти | [a,b] |.
Решение. | [a,b] | =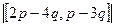 
=
= 
=
= 
= 
= 
.
Ответ. .
