Формула вычисления элементов обратной матрицы: 
.
Алгоритм нахождения 
.
1. Проверить невырожденность с помощью определителя.
2. Составить матрицу из дополняющих миноров Mij.
3. Изменить знаки в шахматном порядке, то есть домножить на (-1)i+j, где i,j - номера строки и столбца.
4. Транспонировать полученную матрицу.
5. Поделить на определитель исходной матрицы.
Задача 1. Найти обратную матрицу для 
.
Решение. 1). Проверяем определитель 
, так что обратная матрица существует.
2) Составляем матрицу из дополняющих миноров, то есть для каждой клетки вычёркиваем строку и столбец, остаётся подматрица порядка 1, то есть то число, которое напротив, как раз и является дополняющим минором. Получаем 
.
3) В шахматном порядке меняем знак там, где i+j нечётное.
Тем самым, мы переходим от 
к 
. Получили 
.
4) Транспонируем эту матрицу. 
.
5) Определитель был равен 1. Делить на 1 не обязательно, можно автоматически считать, что уже и так разделили.
Ответ. .
В качестве домашнего задания сделать проверку, и потренироваться умножать матрицы.
= = 
.
Матричные уравнения. Пусть А - квадратная матрица 
, 
- матрицы размера 
(чаще всего в таких задачах 
, то есть все рассматриваемые матрицы квадратные), причём 
- неизвестная матрица. Тогда определено умножение 
. Матрицу таким образом. Домножим всё равенство слева на обратную матрицу : 
. Тогда 
, то есть 
.
Задача 2. Решить матричное уравнение , где 
.
Решение. Требуетсянайти , заметим, что матрица А тут в точности такая, для которой мы искали обратную в прошлой задаче.
Так, можно использовать 
.
= 
= 
.
Ответ. 
.
Задача 3. Решить матричное уравнение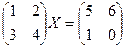 
.
Решение. Сначала найдём обратную матрицу
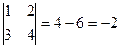. Матрица из миноров: 
.
Матрица из алг. дополнений: 
.
Транспонируем её: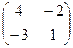 
.
Делим её на определитель, и получаем = 
.
= 
= 
.
Ответ. .
Задача 4. Найти обратную матрицу 
.
Решение. Сначала ищем определитель. Так как матрица треугольная, то достаточно перемножить числа по диагонали. 
.
Строим матрицу, состоящую из дополняющих миноров.
Зачёркиваем ту строку и тот столбец, где находится элемент, и остаётся минор 2 порядка из 4 элементов.
На схеме показано, что именно надо зачеркнуть:
= 
= 
.
Теперь надо сменить знаки в шахматном порядке, т.е. переходим от миноров к алгебраическим дополнениям. Обведено красным, где надо менять знак. Ясно, что 0 остаётся 0, там знак менять нет смысла.
Получили: 
= 
.
Транспонируем эту матрицу, то есть бывшие строки запишем по столбцам.
= 
. И осталось разделить на .
Ответ. 
.
Задача 5. Найти обратную матрицу 
.
Решение. Найдём определитель
.
Найдём матрицу из дополняющих миноров к каждой из 9 клеток.
= 
= 
.
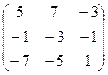Меняем знаки в шахматном порядке, то есть там, где i+j нечётное.
= 
.
Затем транспонируем эту матрицу.
= 
. Осталось только разделить на 
.
Ответ. 
.
Задача 6. Найти обратную матрицу 
.
Решение. Сначала находим определитель.
.
Найдём матрицу из дополняющих миноров.
= 
= 
.
Меняем знаки в шахматном порядке, там, где i+j нечётное.
= 
.
Затем транспонируем эту матрицу.
= 
. Затем делим на 
.
Ответ. 
= 
.
Задача 7. Матричным методом решить систему уравнений:
Решение. Запишем систему в виде: 
.
Обратите внимение, что основная матрица системы это та самая матрица, для которой мы нашли обратную в прошлой задаче.
Если у нас есть равенство 
, то 
, тогда 
.
= 
= 
.
Ответ. 
=1, 
=1, 
=0.
Задача 8. Найти обратную матрицу 
.
Решение. Сначала вычислим определитель: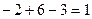 
.
= 
= 
.
= 
, = 
.
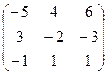Исходный определитель был равен 1, так что делить не нужно.
Ответ. .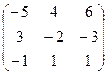
Задача 9. Теоретическое упражнение на тему «единственность обратной матрицы». Доказать, чтоне существует различных обратной слева и справа, то есть, если 
и 
, то 
.
Решение. Пусть и . По закону ассоциативности, можно записать такое равенство: 
.
Но тогда получается 
, то есть .
Задача 10. Найти обратную матрицу 
.
Решение. Найдём определитель: 
.
= 
= 
.
= 
, = 
.
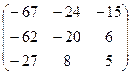Осталось разделить на 
.
Ответ. 
.
Практика 5. Ранг матрицы.
Задача 1. Найти ранг матрицы. 
.
Решение.
Метод 1. Выбираем окаймляющие миноры, начиная от левого верхнего угла. Видно, что минор 2 порядка не равен 0, поэтому ранг больше или равен 2. 
.
Вычисляя минор 3 порядка (а он здесь единственный, это и есть сам определитель матрицы) видим, что он равен 0.
. Тогда раен не равен 3.
, но при этом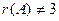 
. Остаётся единственный вариант: 
.
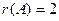Метод 2. Преобразуем матрицу к треугольному виду.
Вычитаем из 2-й строки 1-ю, и из 3-й удвоенную 1-ю.
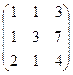
Теперь 2-ю строку, умноженную на 0,5, прибавим к 3-й.
Теперь видно, что 3-я строка состоит из нулей, поэтому ранг не может быть равен 3. Минор 2-го порядка тоже сразу виден, это 
.
Ответ. .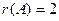
Задача 2. Найти ранг матрицы 
.
Решение. Поменяем 1-ю и 2-ю строки, так чтобы в верхнем левом углу было число 1. Это удобнее для преобразований к треугольной форме методом Гаусса. Ранг при этом не меняется. После этого, вычтем 1-ю строку с коэффициентом 1 либо 4 из последующих, так, чтобы обнулить всё ниде углового элемента.
Ещё мы поменяли 2 и 3 строку, чтобы продолжить метод Гаусса без излишних дробных коэффициентов.
Теперь 2-ю строку, домноженную на 10, прибавим к 3-й.
.
Итак, исходная матрица сводится к такой, в которой уже есть треугольная сруктура в первых трёх столбцах.
Очевидно, что обведённый минор равен 46, не равен 0. Он 3-го порядка, поэтому ранг равен 3.
Ответ: 
.
Задача 3. Найти ранг матрицы и базисный минор. 
.
Решение. Преобразуем матрицу:
Сначала из 2 строки вычитаем 1-ю, домноженную на 2, то есть вычитаем строку (2 4 6) а из 3-й 1-ю, домноженную на 5, т.е. строку (5 10 15). Затем к 3-й прибавляем 20ю с коэффициентом 7.
Видно, что базисный минор не может быть в левом верхнем углу, потому что во 2-й строке два нуля. Зато можно найти минор 2 порядка, состоящий из частей 10и 3 столбца, либо 2 и 3-го.
Минор порядка 3, то есть сам определитель всей этой матрицы, равен 0, так как третий столбец содержит только нули. Поэтому ранг равен 2, а не 3.
Ответ. .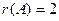
Задача 4. Найти ранг матрицы 
.
Решение. Преобразуем матрицу. Ко второй строке прибавим 1-ю, а от 3-й отнимем удвоенную 1-ю. 
теперь к третьей прибавим вторую, получим 
.
Ранг равен 3, так как есть невырожденный минор 3 порядка.
Ответ. .
Задача 4а (вариант с параметром).
Найти параметр 
, при котором ранг матрицы
равен 2. 
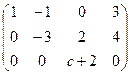
Третья строка сосотяла бы из всех нулей, только если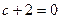 
, то есть 
. То есть, если бы на месте a33 изначально было число -2, то ранг был бы меньше, так как в итоге получилась бы третья строка из всех нулей.
Ответ. .
Задача 5. Доказать, что 3 столбец матрицы
является линейной комбинацией первых двух, и найти коэффициенты этой комбинации.
Решение. Во-первых, если вычислить определитель и обнаружить, что он равен 0, то этим самым уже доказана линейная зависимость столбцов. Однако требуется найти коэффициенты, поэтому запишем систему уравнений:
Прибавим удвоенное 1-е уравнение ко 2-му, и вычтем утроенное 1-е из 3-го.
отсюда видно, что 
, тогда 
.
Ответ. коэффициенты линейной комбинации равны 1 и 2.
Задача 6. Найти ранг матрицы 
.
Решение. Преобразуем методом Гаусса к треугольной форме.
.
Видно, что 4-я строка из нулей, поэтому ранг не равен 4, то есть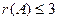 
. Минор порядка 2 легко находится в верхнем левом углу, но угловой минор порядка 3 равен 0. Однако это ещё не значит, что ранг равен 2, ведь можно отступить к правмому краю матрицы и взять минор с разрывом, из 1,2,4 столбцов, например такой:
Этот минор невырожденный, и он тоже является окаймляющим (ведь он полностью включает в себя квадрат, закрашенный жёлтым). Мы нашли базисный минор порядка 3. Также можно было рассматривать аналогичное в 1,2,5 столбцах, тоже минор порядка 3.
Ответ. .
Задача 7. Найти такие параметры 
, что ранг матрицы равен 1:
Решение. Преобразуем методом Гаусса к треугольной форме.
.
Если 
и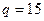 
, то две последних строки только из нулей, и равен будет равен 1.
Ответ. , .
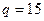Задача 8. Найти ранг матрицы (4*4, можно с произвольными элементами, заданными группой).
Решение. Для удобства преобразования методом Гаусса, сначала поменяем местами 1 и 3 строки. Ещё можно сразу прибавить 3-ю строку к 4-й.
Дальше стандартным методом, обнулим всё ниже угла.
Для удобства вычислений домножим 2 строку на (-1), ранг при этом не меняется. Затем прибавим к 3 строке удвоенную 2-ю.
Теперь осталось прибавить к 4 строке удвоенную 3-ю.
. Видно, что получилась треугольная матрица, то есть определитель 4 порядка невырожденный. Поэтому 
.
Ответ. .
