№ 1. В отрасли работают 10 фирм с одинаковыми функциями затрат TCi = 4 + 2 qi + 0,5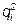 
. Отраслевой спрос задан функцией: QD = 52 – 2 P. Собственник одной из фирм предложил своим конкурентам передать ему все предприятия, обещая за это выплачивать им регулярный доход, в 2 раза превышающий получаемую ими прибыль.
1. Насколько возрастет прибыль инициатора монополизации отрасли, если его предложение будет принято?
2. Насколько сократятся излишки потребителей?
Решение
1. Определим функцию предложения отдельной фирмы 2 + qi = P Þ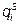 
= –2 + P.
Тогда совместное предложение 10 фирм:
.
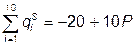В отрасли установится равновесие при:
– 20 +10 Р = 52 – 2 Р Þ P =6; Q = 40; qi =4; p = 6×4 – 4 – 2×4 – 0,5×16 = 4.
Когда все фирмы будут принадлежать одному продавцу, цена определиться из равенства MR = MC. При выведении функции затрат монополии нужно учитывать, что Q = 10 qi. Поэтому TC = 20 + 0,2 Q + 0,5(Q /10)2 = 20 + 0,2 Q + 0,05 Q2; тогда из условия максимизации прибыли получаем:
26 – Q = 0,2 + 0,1 Q Þ Q = 23,45; Р = 14,27.
Прибыль монополиста:
p = 15,1×21,82 – 40 – 2×21,82 – 0,05×21,822 = 222.
После выплат каждому из бывших конкурентов по 8 ден. ед. у монополиста останется (222 – 72) = 150, то есть его прибыль возрастет в 150/4 = 37,5 раза.
2. Излишки потребителей в результате монополизации отрасли сократились с 400 до 119 ден. ед.
№ 2. При линейной функции спроса монополия получает максимум прибыли, реализуя 10 ед. продукции по цене 24 ден. ед. Функция общих затрат монополии
TC = 100 + 4 Q + 0,25 Q 2.
1. Насколько возрастет цена, если с каждой единицы товара будет взиматься налог в размере 7 ден. ед.?
2. На сколько изменится прибыль монополии до уплаты акциза?
3. Какова сумма получаемого налога?
4. На сколько сократятся излишки потребителей?
5. На сколько возрастет объем продаж, если при наличии указанного налога потребители при каждой цене будут спрашивать на 7 ед. товара больше?
Решение
1. Определим значение eD и выведем функцию отраслевого спроса
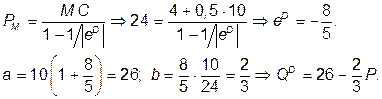
Поскольку в исходных условиях MC = 4 + 0,5 Q, то после введения акциза MC = 11 + 0,5 Q; максимум прибыли монополия получает при 11 + 0,5 Q = 39 – 3 Q Þ
Q * = 8; P * = 27, то есть цена возросла на 3 ден. ед.
2. В исходных условиях p = 24×10 – 100 – 40 – 25 = 75; После введения акциза p = 27×8 – 100 – 32 – 16 = 68. Таким образом, прибыль уменьшилась на 7 ден. ед.
3. Сумма налога: (8×7) = 56 ден. ед.
4. Теперь отраслевой спрос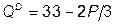 
, а
MR = 49,5 – 3 Q. Максимум прибыли монополия получает при 11 + 0,5 Q = 49,5 – 3 Q Þ Q * = 11; P * = 33, то есть объем продаж возрос на 3 ед.
№ 3. Монополия может продавать продукцию на двух сегментах рынка с различной эластичностью спроса:
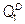=160 – P 1; 
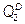= =160– 2 P 2. Ее функция общих затрат TC = 10 + 12 Q + 0,5 Q 2.
1. При каких ценах на каждом из сегментов рынка монополия получит максимум прибыли?
2. Сколько продукции продавала бы монополия на каждом из сегментов в случае запрета ценовой дискриминации?
3. Сколько продукции продавала бы монополия на каждом из сегментов при запрете ценовой дискриминации, если бы ее затраты были в 2 раза меньше?
Решение
1. Условие максимизации прибыли при осуществлении ценовой дискриминации
третьей степени следующее:
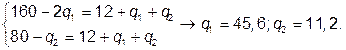
Оптимальные цены на сегментах рынка
P 1 = 160 – 45,6 = 114,4; P 2 = 80 – 0,5×11,2 = 74,4.
2. Для определения условий достижения максимума прибыли при запрете ценовой дискриминации выведем функцию суммарного спроса:
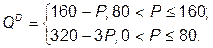
Соответственно
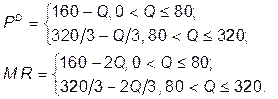
В этом случае линия MC = 12 + Q пересекает MR в интервале 0 < Q £ 80; выпуск и цена определяются из равенства 160 – 2 Q = 12 + Q Þ Q * = 148/3; P * = 332/3. Таким образом, в случае запрещения ценовой дискриминации на втором сегменте рынка продукция продаваться не будет.
3. Теперь кривая предельных затрат MC = 6 + 0,5 Q пересекает ломаную MR два раза
160 – 2 Q = 6 + 0,5 Q Þ Q * = 61,6; P * = 98,4; p = 98,4×61,6 – 5 – 6×61,6 – 0,5×61,62 = 3789,56;
320/3 – 2 Q /3 = 6 + 0,5 Q Þ Q * = 86,3; P * = 77,9; p = 77,9×86,3 – 5 – 6×86,3 – 0,5×86,32 = 2476,13.
Следовательно, на втором сегменте рынка продукция опять продаваться не будет.
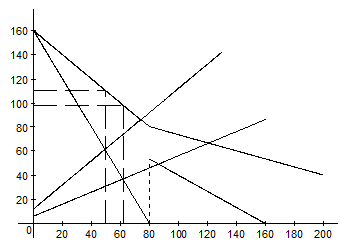
Рис. 9. Ценовая дискриминация третьей степени
№ 4. Спрос на продукцию отображается функцией
QD = 140 – 4 P, а общие затраты на ее производство – функцией TC = 100 + 10 Q + Q 2. Продукция продается на рынке совершенной конкуренции. Во сколько раз должны снизится переменные затраты, чтобы при переходе от совершенной конкуренции к монополии цена не изменилась?
Решение.
Цена при совершенной конкуренции установится на уровне минимума средних затрат. Поскольку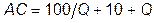 
, то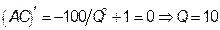 
. Значит, каждая фирма будет выпускать 10 единиц продукции при АС = Р = 30. При такой цене объем рыночного спроса равен 40 ед. Монополия, максимизирующая прибыль, выберет сочетание Р = 30; Q = 40, если при этом предельная выручка равна предельным затратам. Поскольку MR = 40 – 0,5×40 = 20, то производная от переменных затрат тоже должна быть равна 20: (10 + 2×40)/ x = 20 ® x = 4,5; следовательно, переменные затраты должны быть в 4,5 раза ниже, то есть общие затраты TC = 100 + 20 Q /9 + 2 Q 2/9.
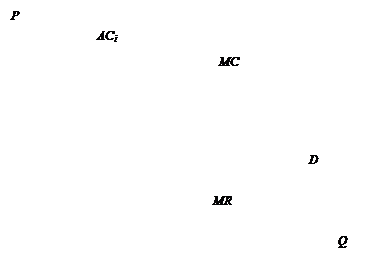
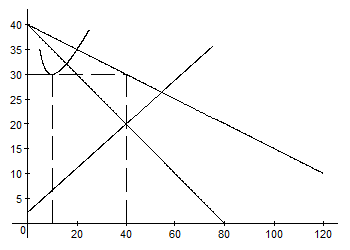
Рис. 10. Конкуренты и монополия
№ 6. В данный момент спрос на продукцию монополистического конкурента отображается функцией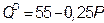 
, а общие затраты – 
.
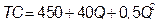Изменение числа конкурентов в отрасли смещает кривую спроса на продукцию фирмы без изменения ее наклона. На сколько сократится выпуск данной фирмы в состоянии длительного равновесия по сравнению с текущим моментом?
Решение
Цена в исходных условиях выводится из равенства MR = MC:
220 – 8 Q = 40 + Q ® Q = 20; P = 140.
В длительном периоде линия отраслевого спроса станет касательной к кривой средних затрат (АС = Р) и сохранится равенство MR = MC. Из системы этих двух равенств определяются запретительная цена периода (обозначим ее x) и выпуск:
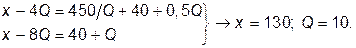
Следовательно, выпуск фирмы сократиться вдвое.
 |
Рис. 11. Монополистический конкурент в коротком и длительном периодах
№ 7. Отраслевой спрос задан функцией P = 50 – 0,25 Q; в отрасли работают две максимизирующие прибыль фирмы I иII со следующими функциями затрат: TC I = 10 + 0,15 q2 I и TC II= 25 + 10 q II. Какая установится цена в соответствии с: а) моделью Курно? б) моделью Штакельберга? в) картельным соглашением?
Решение
а) выведем уравнение реакции для фирмы I. Ее прибыль pI = 50 q I – 0,25 q2 I – 0,25 q I q II – 10 – 0,15 q2 I достигает максимума при 50 – 0,8 q I – 0,25 q II = 0. Поэтому уравнение реакции фирмы I имеет следующий вид:
q I = 62,5 – 0,3125 q II.
Прибыль фирмы II pII = 50 q II – 0,25 q2 II – 0,25 q I q II – 25 – 10 q II и достигает максимума при 40 – 0,25 q I – 0,5 q II = 0. Отсюда выводится ее уравнение реакции: q II = 80 – 0,5 q I.
Если фирмы ведут себя как равноправные конкуренты, то равновесные значения цены и объемов предложения определятся из следующей системы уравнений:
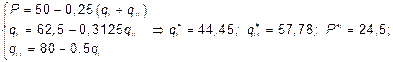
В состоянии равновесия прибыли фирм соответственно будут:
pI = 24,5×44,44 – 10 – 0,15×44,442 = 780,4;
pII = 24,5×57,78 – 25 – 10×57,78 = 809,9.
б) пусть фирма I выступает в роли лидера, а фирма II –последователя. Тогда прибыль фирмы Iс учетом уравнения реакции фирмы II будет:
pI = 50 q I – 0,25 q2 I – 0,25 q I(80 – 0,5 q I) – 10 – 0,15 q2 I = 30 q I – 0,275 q2 I – 10.
Она достигает максимума при 30 – 0,55 q I = 0. Отсюда:
q I= 54,54; q II = 80 – 0,5×54,54 = 52,7;
P = 50 – 0,25(54,54 + 52,7) = 23,2;
pI = 23,2×54,54 – 10 – 0,15×54,542 = 809;
pII = 23,2×52,7 – 25 – 527 = 529.
Таким образом, в результате пассивного поведения фирмы II ее прибыль снизилась, а фирмы I возросла.
В случае лидерства фирмы II ее прибыль
pII = 50 q II – 0,25 q2 II – 0,25 q II(62,5 – 0,3125 q II) – 25 – 10 q II = = 24,4 q II – 0,17 q2 II – 25
становится максимальной при 24,4 – 0,34 q II = 0 Þ q II = 70,9. Тогда
q I = 62,5 – 0,3125×70,9 = 40,3;
P = 50 – 0,25(40,3 + 70,9) = 22,2;
pI = 22,2×40,3 – 10 – 0,15×40,32 = 641;
pII = 22,2×70,9 – 25 – 709 = 840.
в) прибыль картеля определяется по формуле:
pк = (50 –0,25 q I – 0,25 q II)×(q I + q II)– 10 – 0,15 q 2I – 25 – 10 q II =
= 50 q I – 0,4 q2 I – 0,5 q I q II + 40 q II– 0,25 q 2II – 35.
Она принимает максимальное значение при
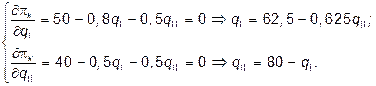
Решив эту систему уравнений найдем
q I = 33,3; q II = 46,7; Q = 80; P = 30; pI = 823; pII = 908.
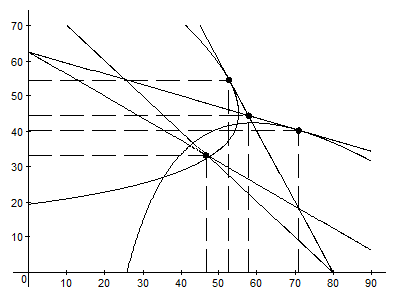
Рис. 12. Зависимость конъюнктуры рынка от типа поведения дуополистов
№ 8. В отрасли функционируют 80 мелких фирм с одинаковыми функциями затрат TCi = 2 + 8 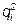, и еще одна крупная фирма, выступающая в роли лидера, с функцией затрат TC л = 20 + 0,275 
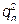. Отраслевой спрос представлен функцией QD = 256 – 3 P. Какая цена сложится на рынке и как он будет поделен между лидером и аутсайдерами?
Решение
Поскольку для аутсайдеров цена является экзогенным параметром, то условием максимизации прибыли для них служит равенство MCi = P. Выведем из него функцию предложения отдельного аутсайдера: 16 qi = P Þ 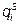= P /16. Тогда суммарная функция предложения аутсайдеров 
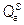= 80 P /16 = 5 P. Теперь определим функцию спроса на продукцию лидера как разность между отраслевым спросом и предложением аутсайдеров: 
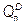= QD – 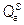= 256 – 3 P – 5 P = 256 – 8 P. В соответствии с этой функцией предельная выручка MR л = 32 – 0,25 Q л. Прибыль лидера максимальна при MR л = MCл:
32 – 0,25 Q л = 0,55 Q л Þ Q л = 40; P = 32 – 0,125×40 = 27. По такой цене аутсайдеры предложат 5×27 = 135 ед. продукции. Объем спроса составит (256 – 3×27) = 175; таким образом, 22,8% спроса удовлетворит лидер и 77,2% – аутсайдеры.
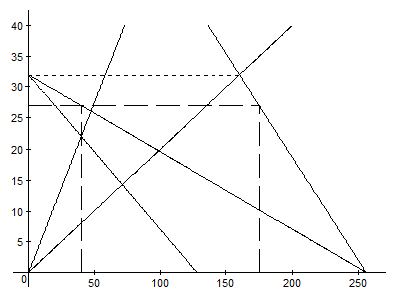
Рис. 13. Ценообразование за лидером
№9. На рынке с отраслевым спросом QD = 100 – 2 P установилась монопольная цена вследствие того, что продавцы образовали картель с общими затратами TC = 72 + 4 Q. После того, как руководству картеля стало известно, что еще одна фирма с такими же общими затратами намеревается войти в отрасль, картель решил снизить цену на столько, чтобы у потенциального конкурента исчезло желание входить в отрасль.
1. Какую максимальную цену может установить картель в этой ситуации?
2. Какой минимальной суммой прибыли придется поступиться картелю?
Решение
1. Искомая цена должна быть такой, чтобы остаточный спрос (неудовлетворенная часть рыночного спроса) оказался ниже кривой средних затрат (PD ост £ AC). Для этого к кривой средних затрат нужно провести касательную, параллельную линии рыночного спроса. Поскольку касательная имеет общую точку с кривой AC и в точке касания наклон обоих линий одинаковый, то искомая цена определяется из решения системы уравнений
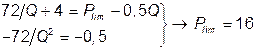
Функция остаточного спроса QD = 32 – 2 P лежит ниже кривой АС.
2. Определим прибыль картеля до появления угрозы потенциального конкурента:
50 – Q = 4 ® Q = 46; Р = 27; p = 27×46 – 72 – 4×46 = 986
и при лимитной цене: 16×68 – 72 – 4×68 = 744; следовательно, Dp = 242.
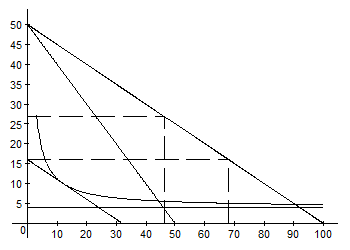
Рис. 14. Лимитная цена картеля
№ 10. В регионе имеется единственное овощехранилище, закупающее картофель у 50 фермеров, выращивающих картофель с одинаковыми затратами TCi = 5 + 0,25 q 2 i, где qi – количество выращенного картофеля i -м фермером. Хранилище сортирует и фасует картофель по технологии, отображаемой производственной функцией
Qf = 16 Q 0,5, где Qf – количество расфасованного картофеля; Q = S qi – количество закупленного картофеля. Определите закупочную цену картофеля при стремлении овощехранилища к максимуму прибыли, если: а) оно может продавать любое количество картофеля по фиксированной цене Pf = 20; б) спрос на фасованный картофель отображается функцией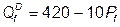 
.
Решение
а) чтобы получить функцию затрат овощехранилища, нужно вывести функцию цены предложения картофеля. Функция предложения каждого фермера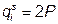 
. Следовательно, рыночное предложение QS = 100 P, соответственно PS = Q/ 100. Тогда общие затраты TCxp = 0,01 Q 2, а прибыль p хр = 20×16 Q 0,5 – 0,01 Q 2. Она достигает максимума при Q = 400. Такое количество картофеля можно закупить по цене PS = 400 / 100 = 4.
б) определим выручку и прибыль овощехранилища:
Pf Qf = (42 – 0,1 Qf ) Qf = (42 – 0,1×16 Q 0,5)×16 Q 0,5.
p хр = (42 – 0,1×16 Q 0,5)×16 Q 0,5 – 0,01 Q 2.
Прибыль достигает максимума при Q = 140. Цена предложения такого количества PS = 140 / 100 = 1,4.
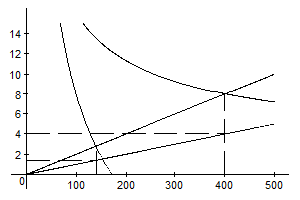
Рис. 15. Цена монопсонии
№ 11. В городе имеется единственный молокозавод, закупающий молоко у двух групп фермеров, различающихся затратами на литр молока стандартной жирност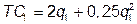и: 
и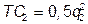 
, где qi – количество молока произведенного одним фермером i –й группы. В первой группе 30 фермеров, во второй – 20. Молокозавод обрабатывает молоко по технологии, отображаемой производственной функцией Qu = 8 Q 0,5, где Qu – количество пакетов молока; Q = S qi – количество закупленного молока, и может продавать любое количество молока по фиксированной цене Pu = 10. При закупке сырья молокозавод может проводить ценовую дискриминацию.
1. По какой цене молокозавод должен закупать молоко у каждой группы фермеров для максимизации своей прибыли?
2. Какую цену установил бы молокозавод, если бы нельзя было проводить ценовую дискриминацию?
Решение
1. Выведем функции цен предложения каждой группы фермеров; эти функции для молокозавода являются функциями средних затрат при закупке молока у соответствующей группы фермеров.
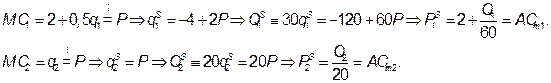
Прибыль завода есть разность между выручкой и общими затратами:
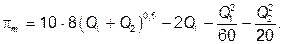
Она достигает максимума при:
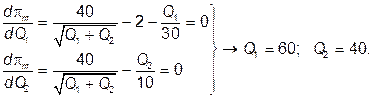
У первой группы фермеров такое количество молока можно купить по 2 + 60/60 = 3, а у второй – по 40/20 = 2 ден. ед.
 |
Рис. 16. Ценовая дискриминация монопсонии
2. В этом случае функция предложения молока имеет вид:
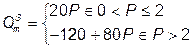
Соответственно, функция цены предложения (функция средних затрат завода):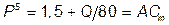 
. Прибыль завода:
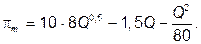
Она достигает максимума при
.
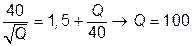Такое количество молока можно купить за 1,5 + 100/80 = 2,75 ден. ед. По такой цене первая группа фермеров предложит 55, а вторая – 45 литров.
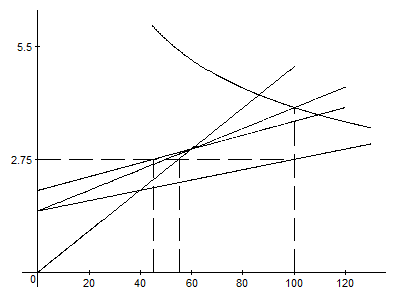
Рис. 17. Единая цена монопсонии на двух сегментах рынка
Задачи
№ 1. Отраслевой спрос представлен функцией: QD = 52 – P. В отрасли работают 6 конкурирующих фирм с одинаковыми затратами: TCi = 9 + 10 qi + 4 q 2 i, где q i – объем выпуска одной фирмы; для других фирм вход в отрасль закрыт. Собственник одной из фирм уговорил четырех других отдать ему свой бизнес, обязавшись выплачивать им ренту, на 1/9 превышающую получаемую ими прибыль от производства.
1. На сколько больше прибыли после выплаты ренты будет оставаться у собственника-монополиста по сравнению с той, которую он получал в роли конкурента?
2. Какая цена установится в длинном периоде, если при неизменных издержках производства отрасль станет открытой?
3. Сколько фирм будет работать в открытой отрасли?
№ 2. При линейной функции спроса монополия получает максимум прибыли, продавая 12 ед. продукции по цене 40 ден. ед. Функция общих затрат монополии TC = 50 + 10 Q + 0,5 Q 2.
1. На сколько возрастут суммарные излишки производителей и потребителей, если при тех же затратах продукция будет продаваться в условиях совершенной конкуренции?
2. На сколько снизится цена монополии, если за каждую проданную единицу продукции ей доплачивать 5 ден. ед?
3. На сколько с учетом дотации увеличится чистый доход монополии?
№ 3. Монополия может продавать продукцию на двух сегментах рынка с различной эластичностью спроса:
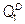= 200 – 4 P 1; 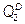= 160 – 2 P 2. Ее функция общих затрат TC = 10 + 12 Q + 0,5 Q 2.
1. При каких ценах на каждом из сегментов рынка монополия получит максимум прибыли?
2. Какую цену установит монополия в случае запрета ценовой дискриминации?
№ 4. Потребности жителей города в молоке отображаются функцией
QD = 280 – 4 P и удовлетворяются одним заводом с функцией общих затрат
TC = 100 + 10 Q + 0,25 Q 2. Половина жителей города – дети. За каждый проданный детям литр молока муниципалитет платит заводу 10 ден. ед.
1. Как молокозаводу распределить свой выпуск между детьми и взрослыми, чтобы получить максимум прибыли?
2. Какая цена будет установлена для детей и для взрослых?
3. Насколько меньше молока производил бы завод без дотации?
№ 5. Отраслевой спрос QD = 180 – 2 P удовлетворяет единственная фирма с функцией общих затрат: TC = 120 + 12 Q + 0,5 Q 2.
1. Определите цену и объем продаж, если фирма максимизирует: а) прибыль; б) выручку; в) объем продаж.
2. Насколько максимальная прибыль превышает прибыль при максимизации объема продаж?
3. Определите величину дотации за каждую проданную единицу товара, при которой фирма, стремясь максимизировать прибыль, будет продавать 45 ед.
4. Определите цену и объем продаж, если фирма максимизирует при наличии 20%-го налога на выручку.
№ 6. Спрос на продукцию монополии, максимизирующей прибыль, отображается функцией QD = 240 – 4 P; функция общих затрат TC = 120 + 10 Q + Q 2. На сколько изменится выпуск монополии, если установить верхний предел цены: а) Р = 52; б) Р = 50; в) Р = 48.
№ 7. Функция спроса на продукцию естественной монополии: QD = 6 – 0,1 P; функция общих затрат
TC = 48 Q + 12 Q 2 + Q 3.
1. Определите сумму дотации монополии, чтобы она могла работать безубыточно при директивной цене Р = МС.
2. Насколько меньше был бы выпуск монополии без государственного регулирования цены?
3. Какую минимальную директивную цену можно установить, чтобы монополия могла работать безубыточно без дотации?
№ 8. Спрос на продукцию отображается функцией
QD = 140 – 4 P, а общие затраты на ее производство – функцией TC = 80 + 5 Q + Q 2. Продукция продается на рынке совершенной конкуренции. Во сколько раз должны снизится переменные затраты, чтобы при переходе от совершенной конкуренции к монополии цена не изменилась?
№ 9. Спрос на продукцию монополии отображается функцией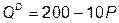 
, а ее затраты функцией 
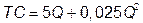. Монополия может проводить ценовую дискриминацию 2-й степени при условии, что 1-я партия продукции состоит из 25 ед.
1. Какую максимальную прибыль может получить монополия в этом случае?
2. На сколько возросла бы прибыль монополии, если бы она могла проводить ценовую дискриминацию 1-й степени?
№ 10. Даны функция затрат монополии и функция спроса: TC = 50 + 20Q, P = 100 – 4Q. Определить объем производства, цену и сумму максимальной прибыли монополии. Как изменится объем производства и сумма прибыли, если монополия будет осуществлять совершенную ценовую дискриминацию?
№ 11. Дана функция спроса монополии: Q = 180 – 2P. Функция общих затрат имеет следующий вид: TC = 2Q2 + 90. Определить объем выпуска и цену, максимизирующие прибыль монополии. Определить объем выпуска, если монополист получит возможность применять совершенную ценовую дискриминацию.
№ 12. Спрос на продукцию монополии отображается функцией 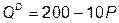. Монополия может производить продукцию на двух предприятиях, различающихся функциями затрат: 
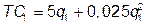и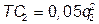 
; q 1 + q 2 = Q. Как распределить выпуск между предприятиями, чтобы прибыль была максимальной?
№ 13
. В данный момент спрос на продукцию монополистического конкурента отображается функцией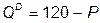 
, а общие затраты – 
.
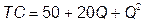Изменение числа конкурентов в отрасли смещает кривую спроса на продукцию фирмы без изменения ее наклона. На сколько в состоянии длительного равновесия: а) снизятся цена и выпуск данной фирмы по сравнению с текущим моментом? б) средние затраты превышают минимально возможные?
№ 14. Отраслевой спрос задан функцией цены спроса P = 200 – Q; в отрасли работают две максимизирующие прибыль фирмы I иII со следующими функциями затрат: TC I = 100 + 0,5 q2 I и TC II= 50 + 40 q II. Определите прибыль каждой фирмы в соответствии с: а) моделью Курно; б) моделью Штакельберга при лидерстве фирмы I; в) картельным соглашением при распределении прибыли пропорционально выпуску.
№ 15. В отрасли функционируют 120 мелких фирм с одинаковыми функциями затрат TCi = 20 + 10 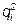, и еще одна крупная фирма, выступающая в роли лидера, с функцией затрат TC л = 50 + 0,5 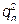. Отраслевой спрос отображается функцией QD = 400 – 2 P.
1. Определите прибыль лидера и каждого из аутсайдеров.
2. Вследствие увеличения доходов покупателей они стали спрашивать на 40 ед. товара больше. На сколько возрастет объем продаж и как прирост выпуска распределится между лидером и аутсайдерами?
№ 16. Отраслевой спрос отображается функцией
QD = 256 – 3 P. В отрасли функционируют одна крупная фирма, выступающая в роли лидера, с функцией затрат TC л = 50 + 0,25 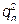и мелкие фирмы-аутсайдеры с одинаковыми функциями затрат TCi = 2 + 15 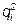. Лидер установил цену Р = 60 и продает 20 ед. продукции. Сколько аутсайдеров работает в этой отрасли?
№ 17. На рынке с отраслевым спросом QD = 120 – P установилась монопольная цена вследствие того, что продавцы образовали картель с общими затратами
TC = 450 + 12 Q + Q 2. После того, как руководству картеля стало известно, что еще одна фирма с такими же общими затратами намеревается войти в отрасль, картель решил снизить цену на столько, чтобы у потенциального конкурента исчезло желание входить в отрасль.
1. Какую максимальную цену может установить картель в этой ситуации?
2. На сколько больше продукции будет продавать картель ввиду потенциальной угрозы конкурента?
№ 18. Монополистический конкурент с функцией общих затрат TC = 300 + 10 Q + 0,5 Q 2 в состоянии длительного равновесия продает свою продукцию по цене Р = 45. До прихода в отрасль новых конкурентов он мог по каждой цене продавать на 12 ед. своей продукции больше. Какова тогда была его прибыль?
№ 19. Монополистический конкурент с функцией общих затрат TC = 300 + 30 Q + 2 Q 2 в состоянии длительного равновесия производит продукцию со средними затратами на 21 ден. ед. больше, чем минимально возможные. 1. Определите цену и объем продаж данной фирмы.
2. Насколько больше продавала бы каждая фирмы, если бы вследствие стандартизации продающегося на рынке продукта монополистическая конкуренция сменилась совершенной конкуренцией?
№ 20. Отраслевой спрос на рынке дуополии представляет функция QD = 70 – 0,5 P; обе фирмы имеют одинаковые затраты: TCi = 20 + q 2 i. На сколько снизится цена, и на сколько возрастет объем продаж, если фирмы перейдут от поведения в соответствии с моделью Курно к поведению в соответствии с моделью Штакельберга?
№ 21. На рынке дуополии спрос существует только при
Р < 50 и достигает полного удовлетворения при Q = 200. Известны уравнения реакции обоих дуополистов, ведущих себя в соответствии с моделью Курно:
q 1 = 60 – 0,25 q 2; q 2 = 100 – 0,5 q 1. Какая цена установится на рынке?
№ 22. На рынке совершенной конкуренции с отраслевым спросом
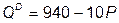торговали фирмы с одинаковыми затратами
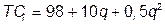. В определенный момент 20 фирм образовали картель, став ценовым лидером.
1. Насколько в результате этого возросла цена и сократился объем продаж?
2. Насколько бы возросла цена и сократился объем продаж, если бы в картель вошли 30 фирм?
№ 23. В регионе имеется единственное овощехранилище, закупающее картофель у 100 фермеров, выращивающих картофель с одинаковыми затратами
TCi = 2 + + 0,25 q 2 i, где qi – количество выращенного картофеля i -м фермером. Хранилище сортирует и фасует картофель по технологии, отображаемой производственной функцией Qf = 8 Q 0,5, где Qf – количество расфасованного картофеля; Q = S qi – количество закупленного картофеля. Определите суммарную прибыль фермеров при стремлении овощехранилища к максимуму прибыли, если: а) оно может продавать любое количество картофеля по фиксированной цене Pf = 20; б) спрос на фасованный картофель отображается функцией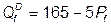 
.
№ 24. В городе имеется единственный элеватор, закупающий зерно у двух групп фермеров, различающихся затратам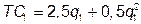и: 
и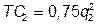 
, где qi – количество зерна произведенного одним фермером i –й группы. В первой группе 40 фермеров, во второй – 20. Элеватор производит муку по технологии, отображаемой производственной функцией Qz = 8 Q 0,5, где Qz – количество муки; Q = S qi – количество закупленного зерна, и может продавать любое количество муки по фиксированной цене Pz = 16. При закупке сырья молокозавод может проводить ценовую дискриминацию. Насколько больше прибыли получит элеватор при проведении ценовой дискриминации по сравнению с закупкой зерна по единой цене?
№ 25. Фирма, находящаяся в условиях монополистической конкуренции сталкивается с функцией спроса при объеме продаж:
| до 10 ед.: | Р = 36 – 0,2Q, |
| от 10 до 20 ед.: | Р = 44 – Q, |
| Более 20 ед.: | Р = 34 – 0,5Q |
Определить объем выпуска, максимизирующий прибыль фирмы, цену, общую сумму прибыли, если функция затрат имеет вид: TC = 70 + 8Q.
№ 26. Монополистический конкурент, производящий продукцию с затратами: TC = 9,5Q, установил, что цена на его продукцию меняется по формуле: P = 23,5 – 0,5Q, если он продает больше 11, по формуле: P = 25 – 1/3Q, если он продает не больше 6 ед., по формуле: P = 29 – Q, если он продает больше 6, но не больше 11 ед.
Определить объем выпуска данной фирмы, максимизирующий прибыль, и размер этой прибыли.
№ 27. Функция спроса на продукцию фирмы имеет вид:
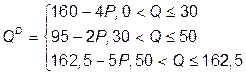
а функция общих затрат – TC = 50 + 12 Q + 0,125 Q 2.
1. При какой цене прибыль фирмы максимальна?
2. Насколько изменится цена при взимании акциза в размере 2 ден. ед. с каждой проданной единицу продукции?
3. Насколько изменится цена при предоставлении дотации в размере 1 ден. ед. за каждую проданную единицу продукции?
4. Определите максимум прибыли при TC = 500 + 0,05 Q 2.
