Опыт показывает, что ни одно измерение, как бы тщательно оно ни проводилось, не может быть выполнено без ошибок. В лабораторном эксперименте необходимо свести ошибки к минимуму и надежно рассчитать их величины.
КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ И ОШИБОК
Измерения используются как средство регистрации физических величин непрерывного типа (расстояний, времени, веса и т.д.).
Прямыми измерениями называются такие, результаты которых получаются при непосредственном сравнении измерений величины с принятой единицей измерения, например, измерение времени секундомером, длины – линейкой и т. д.
Косвенным называется измерение, при котором искомое значение величины находят на основании зависимости между этой величиной и величинами, найденными в результате прямых измерений. Например, вычисление объема параллелепипеда по измеренным его сторонам, вычисление числа Рейнольдса и средней скорости и т.д.
Ошибки можно классифицировать по закономерностям появления.
Случайной называется такая ошибка, которая изменяется от одного измерения к другому непредсказуемым образом. Случайная ошибка возникает как результат совместного влияния различных случайных факторов.
Систематической называется такая ошибка, которая остается постоянной на протяжении одной серии измерений.
ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТЕЙ В ПРИБОРАХ
Удобный способ представления результата любого измерения состоит в том, что указывается наилучшая оценка измеренной величины и интервал, в котором она лежит.
В общем случае результат измерения величины X приводится так:
Х=Хнаил.±δХ.
а) наилучшая оценка для измеренной величины есть число Хнаил;
б) экспериментатор до определенной степени уверен, что значение измеренной величины находится между Хнаил. + δХ и Хнаил.- δX.
Число δХ называется погрешностью или ошибкой измерения.
Погрешность δХ принято считать положительной величиной, так что Хнаил.+δХ есть всегда вероятное наибольшее значение измеряемой величины, а Хнаил.-δХ – наименьшее.
Предположим, что производим n измерений величины Х (используя одну и ту же аппаратуру и один метод измерений) и получаем n значений Х1,Х2,…,Хn. Полученной оценкой будет:
(а)
Обычно минимальное число измерений принимается равным 4-5. В теории вероятности строго доказывается, что при этом значение 
будет более надужным, чем любое из отдельных измерений, при этом погрешность при измерении величины Х равна δХ=σх. Величина σх называется стандартным отклонением среднего и определяется по формуле:
(б)
где N – число измерений. Можно записать 
ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ
Как было сказано выше, погрешность в измерении:
показывает надежность или точность измерения. Однако погрешность в 1 мм для расстояния 100 м означало бы необычайно точное измерение, в то же время погрешность 1мм для расстояния 3 мм означало бы грубую оценку. Поэтому очевидно, что качество измерения характеризуется не только самой погрешностью δХ, но также и отношением δХ к 
, и этот факт заставляет нас рассматривать относительную погрешность, которая называется также точностью.
Относительная погрешность приближенно характеризует качество измерений независимо от значения измеряемой величины.
Относительная погрешность = 
ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТЕЙ В КОСВЕННЫХ ИЗМЕРЕНИЯХ
Большинство физических величин невозможно измерить непосредственно, и их определение включает два различных этапа. Сначала измеряют одну или более величины х, у, ..., которые могут быть непосредственно измерены. Затем, используя измеренные значения х, у, ... вычисляют саму искомую величину:
Z=α(x,y, …,w).
Предположим, что произведены измерения величин х, у, ... с соответствующими погрешностями δх, δу, и что теперь необходимо по измеренным значениям х, у,... вычислить величину z, которая нас интересует.Задача, которую мы должны решить, заключается в том, каким образом погрешности δх, δу, «распространяясь» через вычисления, приводят к погрешности δz косвенных измерений относительной величины z.
СУММЫ И РАЗНОСТИ
Если несколько величин х,...,w измерены с погрешностями δх...δw и используются для вычисления g=х+...+g-(u+...+w), то погрешности в рассчитанной величине есть сумма δz ≈ δх+... δg+ δu+...+ δw всех исходных погрешностей.
ПРОИЗВЕДЕНИЯ И ЧАСТНЫЕ
Если несколько величин х,..w измерены с погрешностями δх... δw и измеренные значения используются для расчета 
то относительная погрешность величины z равна сумме относительных погрешностей в х,...w:
УМНОЖЕНИЕ НА ЧИСЛО
Измеренное число умножается на точное число. Если величина x измерена с погрешностью δх и используется для вычисления произведения z=Вх, в котором В не имеет погрешности, то погрешность в z равна |В|, умноженному на погрешность в х: δz=|В|δх.
ВОЗВЕДЕНИЕ В СТЕПЕНЬ
Если величина х измеряется с погрешностью δх и измеренное значение используется для вычисления степени этого числа z=xn, то относительная погрешность в z в n раз больше относительной погрешности в х:
ТАБЛИЦА ВЕЛИЧИН ПОГРЕШНОСТЕЙ
| Математическая операция | Абсолютная погрешность | Относительная погрешность |
| N=А+В+С+... | ±(∆А+∆В+∆С+...) | 
|
| N=А-В | ± (∆А+∆В) |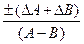 
|
| N=А•В | ± (В∆А+А∆В) | ±(∆А/А+∆В/В) |
| N=A•B•C | ± (ВС∆А+АС∆В+АВ∆С) | ± (∆А/А+∆В/В+∆С/С) |
| N=А1/n | ±А1\n-1 | 
|
| N=Аn | ±nАn-1∆А | ±n∆А\А |
| N=А/В | ± (В∆А+А∆В)/В2 | ± (∆А/А+∆В/В) |
| N=sin(A) | ± соs(А)∆А | ± ctg(А)∆А |
| М=cos(A) | ± sin(А)∆А | ± tg(А)∆А |
Пример 7. Расход измеряется три раза и получаются следующие значения:
W1 = 2020 см3, t1 =16 с,
W2 =2558 см3, t2 =20 c,
W3 =1612 см3, t3 =13 с,
Q1= W1/ t1 =126,2 см3/с,
Q2= W2/ t2 =127,9 см3/с,
Q3= W3/ t3 =124 см3/с.
В данном случае величины удобно представлять так: объемы – см3, время – с, расход – см3/с, скорость – см/с, ускорение – см/с2, разность показаний пьезометров – см.
Для дальнейших расчетов примем расход, равный среднему арифметическому:
При прохождении потока через местное сопротивление (поворот трубы на 90º) скорость не изменяется и равна:
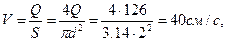
где d – диаметр трубы, равный 20 мм.
Показания первого пьезометра (до местного сопротивления) h1 =72 см, показания второго пьезометра (после местного сопротивления) h2 =68 см, тогда ∆h = 72-68=4 см.
Подставляем все полученные величины в формулу для 
и определяем коэффициент местного сопротивления (для поворота трубы на 90º):
Теперь можно определить число Рейнольдса:
Пример 8. При тех же значениях расхода измерялась разность показаний пьезометров до и после местного сопротивления, представляющего собой внезапное расширение трубы от d1 =20 мм, до d2 =50 мм.
Разность показаний пьезометров ∆h1 =1,7 см, ∆h2 =1,5 см, ∆h3 =1,3 см.
Среднее арифметическое значение ∆h:
Потери напора на этом сопротивлении
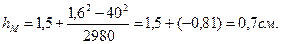
По формуле Борда потери в таком сопротивлении
Коэффициент местного сопротивления (по отношению и скорости V1 =40 cм/с):
Пример 6. При определении нижнего критического числа Рейнольдса (Reн.кр) несколько раз измеряется расход воды объемным способом (с помощью мерной емкости с ценой деления 2 см3 и секундомера с ценой деления 0,2 с).
Требуется найти величины абсолютной и относительной погрешностей при определении Reн.кр.
Решение
Прямыми измерениями в данном случае являются измерения объёма, времени, температуры и диаметра.
Расход измерялся 5 раз с получением следующих результатов:
W1 =865 см3, Q1 =57,7 см3/с, t1 =15 с,
W2 =1174 см3, Q2 =58,7 см3/с, t2 =20 с,
W3 =1417 см3, Q3 =56,7 см3/с, t3 =25 с,
W4 =1298 см3, Q4 =59 см3/с, t4 =22 с,
W5 =1392 см3, Q5 =58 см3/с, t5 =24 с.
Расчетный расход находится как среднее арифметическое из полученных значений по (а):
В полученном результате две цифры после запятой должны быть отброшены, как ненадежные.
Затем вычисляется стандартное отношение для Q по зависимости (б):
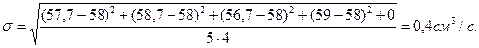
Окончательный результат определения расхода можно записать как Q =58±0,4 см3/с.
Относительная погрешность при определении расхода составит тогда 0,4/58·100% ≈ 1%.
Абсолютная погрешность при определении диаметра равна ±0,01м.
Число Рейнольдса находится по формуле:
Абсолютную и относительную погрешности при определении числа Re нужно найти самостоятельно, приняв, что кинематический коэффициент вязкости ν измерен точно (без заметной погрешности).
