Местными называются такие сопротивления, которые обусловлены каким-либо местным препятствием свободному течению жидкости, например, изгибом трубы или крана, расширением или сужением потока и т.д. Эти сопротивления возникают только в определенных местах потока на незначительном протяжении, на этом участке.
Жидкость, преодолевая местное сопротивление, теряет часть своей энергии, и возникают местные потери энергии (напора).
Потери напора h на местные сопротивления выражаются в долях скоростного напора и определяются по формуле Вейсбаха:
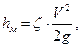 (21)
(21)
где ζ – коэффициент местного сопротивления; V – средняя скорость потока.
Коэффициент местного сопротивления зависит от конструкции (от вида) местного сопротивления и от числа Рейнольдса. При развитом турбулентном режиме (примерно при Rе > 10000) коэффициент ζ от числа Rе практически не зависит, а зависит от конструкции местного сопротивления.
В формуле Вейсбаха в качестве V может быть принята скорость до и после сопротивления, при этом изменится значение коэффициента ζ. Поэтому всегда указывают, относительно какой скорости определяется коэффициент ζ.
Значения коэффициентов местных сопротивлений, полученные опытным путем для различных типов сопротивлений, содержатся в гидравлических справочниках. Течение жидкости в местных сопротивлениях является очень сложным, и определение коэффициентов ζ аналитическим путем практически невозможно, поэтому они определяются из опытов. При экспериментальном определении коэффициентов ζ основными уравнениями являются уравнение неразрывности (5), уравнение Бернулли (7), а также формула (21).
Обращаем внимание на то, что главной задачей является самостоятельное определение коэффициентов местных сопротивлений ζ опытным путем. После решения этой задачи проводится сравнение значений ζ, полученных в опыте, с теми, которые возможно определить по аналитическим зависимостям или по справочникам.
К любому потоку, содержащему местные сопротивления, можно применить уравнение Бернулли (рисунок 8):
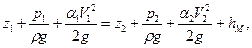
откуда принимаем z 1= z 2, α 1= α 2≈ 1 (труба горизонтальная),

Для определения потерь все экспериментальные величины подставляются в формулу для hM. В частности, показание первого пьезометра (в первом сечении) равно p1/ρg=h1, показание второго пьезометра – p2/ρg=h2, а их разность определяется по шкале (линейке). Средние скорости V1 и V2 определяются по формулам:
 и
и 
где Q – расход; S1 и S2 – площади живых сечений 1 и 2.
Если местное сопротивление таково, что до и после него поток не меняет своего сечения (как на рисунке 8), то в формуле для hM V1=V2 и потери определяются следующим образом:
 (22)
(22)
К сопротивлениям этого типа относятся повороты трубы, вентили различных типов и т. п.
После вычисления потерь в данном местном сопротивлении и выражения их в единицах длины определяется коэффициент местного сопротивления по формуле:

которая преобразуется для этой цели к виду:
 (23)
(23)

Рис. 8
Если скорости до и после местного сопротивления не равны, то есть V1≠V2, то по указанию преподавателя выбирается одна из них (либо V1, либо V2).
Одна из немногих теоретических зависимостей для определения местных потерь – формула Борда для случая внезапного расширения потока (рис. 3):
 (24)
(24)
Для круглых труб формулу Борда можно представить так:
 (25)
(25)
Из (25) следует, что коэффициент местного сопротивления при внезапном расширении имеет вид:
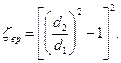 (26)
(26)
При внезапном сужении круглой трубы коэффициент местного сопротивления определятся зависимостью (для квадратичной зоны сопротивления):

 (27)
(27)
Табличные данные: коэффициенты местных сопротивлений для некоторых местных сопротивлений — резкий поворот трубы круглого поперечного сечения ζ =0,2-1,1 для угла поворота α =30-90°, резкий поворот трубы прямоугольного поперечного сечения ζ =0,025-1,2 для угла поворота α = 15-90°, для случая резкого и плавного сужения трубы соответственно ζ =0,5 и ζ =0,03.
Цели работы
1. Определить значения коэффициентов местных сопротивлений.
2. Изучить зависимость коэффициентов местных сопротивлений от числа Рейнольдса.






