Саратовский государственный технический университет
Имени Гагарина Ю.А.
ОБЩАЯ Г И Д Р А В Л И К А
практикум для студентов направления «Строительство»
Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета
имени Гагарина Ю.А.
Саратов 2015
Все права на размножение и распространение в любой форме остаются за разработчиком.
Нелегальное копирование и использование данного продукта запрещено.
Составили: КАЛЯКИН Александр Михайлович
САУТКИНА Татьяна Николаевна
ЧЕСНОКОВА Елена Вадимовна
Рецензент Н.Н.Береда
Редактор К.А. Кулагина
Компьютерная верстка О.А. Духовникова
410054 г.Саратов, ул. Политехническая, 77
Научно-техническая библиотека СГТУ
Тел. 99-86-65, 9986-561
http://lib.sstu.ru
Регистрационный номер №
Саратовский государственный
Технический университет, 2012-02-15
ВВЕДЕНИЕ
Практикум предназначен для выполнения основных лабораторных работ студентами направления «Строительство» всех форм обучения.
Перед выполнением лабораторного практикума все студенты проходят инструктаж по технике безопасности в соответствии с ГОСТ 12.001 ЕСТБ.
Лабораторные работы выполняются небольшими группами по 2- 4 студента.
При подготовке к выполнению лабораторных работ студент обязан:
а) изучить соответствующие разделы теоретического курса (они указаны
в конце каждой работы) или лекций;
б) изучить методику проведения эксперимента;
в) выполнить и уметь формулировать задачи исследования;
г) уметь отвечать на контрольные вопросы (они приведены в методических указаниях в конце описания каждой работы).
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОГО ПРАКТИКУМА
И ОФОРМЛЕНИЯ ОТЧЕТОВ ЛАБОРАТОРНЫХ РАБОТ
Студент обязан самостоятельно изучить соответствующие теоретические разделы курса по учебникам или лекциям и уметь отвечать на контрольные вопросы.
В начале занятия у студентов проверяют подготовленность конспектов, и проводится контроль знаний по системе «Допуск», то есть проверяется, в какой степени студент готов к выполнению лабораторной работы. Студенты, не прошедшие контроль по системе «Допуск», к выполнению работ не допускаются.
План и методика проведения лабораторной работы, а также исходные данные и задание уточняются преподавателем.
Лабораторные работы оформляются в тетради или на отдельных листах. Результаты всех измерений и вычислений, выполненных в работе, заносят в отчетный лист, оформленный в виде таблицы.
ПОРЯДОК ОФОРМЛЕНИЯ (КОНСПЕКТИРОВАНИЯ) РАБОТ
Все перечисленные ниже пункты необходимо выполнить, и они должны в обязательном порядке присутствовать в конспекте. Все остальное содержание методических указаний (описание методики, формулы и т.д.) конспектируется по желанию студента.
1. Название работы.
2. Схема установки.
3. Цели исследования.
4. Отчетный лист (примерный вид его приведен ниже).
| № п/п | Наименование измеряемых величин | Единицы измерения | Числовые значения |
5. Выводы.
Выводы и заключения делаются в произвольной форме. При выполнении вычислений необходимо все физические величины, участвующие в расчетах, привести к одной системе единиц.
На всех стадиях подготовки к выполнению работы студенту необходимо проявить инициативу, творческий подход и стремиться к полному пониманию целей работы и средств их достижения.
ОБЩИЕ ПОЛОЖЕНИЯ
Расходом называется объем жидкости, проходящий через сечения трубопровода в единицу времени. 
При выполнении лабораторных работ для определения расхода применяется объемный способ.
Суть объемного способа в том, что измеряется промежуток времени t, в течение которого жидкость заполняет некоторый известный объем W.
Имеется в виду объемный расход Q, который при установившемся движении определяется по формуле:
 , (1)
, (1)
где W – объем жидкости, поступивший из трубопровода в мерную емкость за время t.
Обычно, если какая-либо величина сравнивается с эталоном или с единицей измерения, то говорят, что она измеряется; например, с помощью линейки возможно измерить длину трубы, с помощью секундомера – время, мерным сосудом (с делениями) измеряют объем воды и т.д.
Если же какая – либо величина получается с помощью вычислений (сложения, вычитания, деления и т.д.), то принято говорить, что она вычисляется или определяется.
Пример 1. В емкость, подставленную под струю из открытого крана некоторое количество воды набралось за 25 секунд (время измерено с помощью секундомера). Набранный объем воды слили в мерную емкость с делениями и оказалось, что объем равен 5375 см3 или 5,375 л. Таким образом, измерены объем W и время t. Для определения расхода Q вычисляется дробь
Q =  = 215 см3/с.
= 215 см3/с.
Средняя скорость определяется по формуле:

 , (2)
, (2)
где S — площадь поперечного сечения трубопровода.
Пример 2. Найти среднюю скорость течения в трубе диаметром d =15 мм, если при измерении расхода Q объемным способом в мерный бак поступил объем W =1080 см3 воды за t =21 с.
Расход Q определяем по формуле:
Q=  =
=  = 51 см3/с.
= 51 см3/с.
Площадь сечения круглой трубы диаметра определяется с помощью известной зависимости:
S= 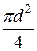 .
.
Окончательно среднюю скорость определяем так:
V=  =
=  =
= 
 = 29 см/с.
= 29 см/с.
Установившимся движением называется такой вид движения, при котором параметры потока не изменяются со временем. Для создания установившегося движения воды в лабораторной установке уровень воды в напорном (верхнем) баке поддерживается постоянным автоматически.
Абсолютное давление р в любом из сечений потока жидкости может быть записано в виде
p= ратм+ризб,
где ратм – атмосферное давление; ризб – избыточное давление (давление столба жидкости высотой h).
Для измерения избыточного давления в лабораторных установках применяют пьезометры. Пьезометр (рисунок 1) представляет собой вертикальную трубку (чаще стеклянную) с открытым в атмосферу верхним концом. Нижний конец присоединен к трубе в том сечении, в котором измеряется давление.

Рис. 1
Величина избыточного пьезометрического давления определяется по формуле:
ризб = ρ·g·h,
где ρ – плотность жидкости; g – ускорение свободного падения; h –пьезометрический напор (пьезометрическая высота).
Таким образом, давление в некотором сечении прямо пропорционально высоте подъема жидкости в пьезометре, установленном в данном сечении. Эта высота обычно измеряется по шкале. На рисунке 1 видно, что давление уменьшается вдоль потока.
Пьезометрическая высота определяется по формуле:
 . (3)
. (3)
При установившемся движении через любое поперечное сечение потока в единицу времени проходит одинаковый объем жидкости, то есть
Q = const, (4)
или
V1S1=V2S2=V3S3=…=VnSn, (5)
где Vn и Sn – средняя скорость и площадь живого сечения.
Поэтому для любых двух сечений, можно записать:
 . (6)
. (6)
Основным уравнением, определяющим связь между давлением и скоростью в потоке жидкости, является уравнение Д. Бернулли.
Записанное для двух сечений 1 и 2, оно имеет вид:
 , (7)
, (7)
где величина α для турбулентных потоков обычно принимает значение 1,04 – 1,13; z – удельная энергия положения (удельная энергия – это энергия, отнесенная к весу жидкости, проходящей через сечение потока за единицу времени); p/ρg – удельная энергия давления; αV2/2g – удельная кинетическая энергия, V – средняя скорость в сечении.
С геометрической точки зрения z – геометрический напор (расстояние от плоскости отсчета 0–0, рис. 1 до оси потока), p/ρg – пьезометрическая высота; αV2/2g – скоростной напор.
Вязкость жидкости зависит от температуры; в частности для величины кинематического коэффициента вязкости чистой пресной воды применяются формула:
ν =  , см2/с,
, см2/с,
где t 0 – температура в градусах по шкале Цельсия.
Пример 3. При температуре воды t0 = 18,2ºС
ν =  см2/с.
см2/с.
Замечание 1. Часто размерность физической величины отождествляют с ее единицей в соответствующей системе единиц. Так, например, говорят, что скорость имеет размерность см/с (сантиметр в секунду). Хотя это и не логично, но грубой ошибки в этом нет. В данном случае см/с – это наименование единицы (точно так же, как км/ч, м/с и т.д.). Размерность физической величины имеет более общий смысл, чем наименование ее в какой-либо системе единиц. Например, размерность ускорения всегда одна L/t2, где L – длина, t – время, но наименования ускорения могут быть разными – в системе СИ м/с2, в системе CGS – см/с2 и т.д. Размерность расхода единственная L3/t (отношение объема ко времени), а наименование его могут быть различными, например м3/час, см3/с и т. д.
Замечание 2. При выполнении работы, всегда необходимо выяснить – какие величины измеряются непосредственно, а какие определяются с помощью вычислений.
Если допускается ошибка при измерении, то она может быть исправлена только при повторном выполнении работы, поэтому процессу выполнения работ придается особое значение. До выполнения лабораторной работы следует продумать последовательность действий и подготовить измерительные инструменты.
Величины, которые определяются, могут быть после выполнения работы многократно проверены и обычно ошибки при этом легко исправляются.
Например, при выполнении работы № 1 «Исследование режимов движения жидкости» измеряются:
1. Температура t0.
2. Диаметр трубки d.
3. Объем жидкости W.
4. Время t, в течение которого через прибор прошёл и был набран в ёмкость объём W.
Затем, после выполнения всех измерений определяются:
1. Расход  ,
,
2. Кинематический коэффициент вязкости по формуле Пуазейля.
3. Площадь сечения трубки  ,
,
4. Средняя скорость  ,
,
5. Число Рейнольдса  .
.
Методика применения уравнения Бернулли.
Уравнение Бернулли является одним из основных в гидравлике и поэтому техника и методика его использования так важны; перечислим основные условия его применения.
1. Выбираются сечения потока, в которых движение является плавно изменяющимся.
2. Назначается положение плоскости сравнения – плоскости отсчета геометрических высот z.
3. При написании уравнения Бернулли для сечений, где движение плавно изменяющееся (где z + p/ρg = const), выбираются точки, для которых записываются высоты положения z и давление p в любом месте назначенных сечений на дне, на свободной поверхности, в центре живого сечения, на оси трубы и т.д. Лучше всего выбирать эти точки или на свободной поверхности (в этом случае чаще всего p1=p2=pат), или в центре тяжести живых сечений тогда может быть сокращен объем вычислений.
4. Имея в виду самый общий вид уравнения Бернулли для потока реальной жидкости, записывают все ее члены применительно к выбранной плоскости отсчета и двум сечениям. В случае успешного применения (совместно с уравнением неразрывности) должно остаться одно неизвестное.
Пример 4. Применить уравнение Бернулли к участку горизонтальной трубы одинакового диаметра, по которой течет вязкая жидкость.
Решение. Действуем непосредственно по только что изложенной методике. В данном случае в любом сечении движение является плавно изменяющимся и поэтому произвольно выберем два сечения, как показано на рисунке.

Рис. 2
Высоты z1 и z2 отсчитывали от центров сечений и давления в сечениях принимали p1 и p2. Расход жидкости в сечениях 1 и 2 одинаковый и в силу постоянства диаметра скорости в сечениях также равны, т.е. V1=V2.
Уравнение Бернулли в общем виде:
 .
.
Применительно к данному случаю имеем: z1=z2 =0, V1=V2 и уравнение Бернулли принимает вид: ∆h = (p1 – p2)/ρg = h W .
Величины пьезометрических высот p1/ρg и p2/ρg представляют высоты столбов жидкости в пьезометрах трубках с открытыми концами, установленных в первом и во втором сечениях. Потери всегда положительны, т.е. hW >0, поэтому высота жидкости в левом пьезометре больше, а разность ∆h точно равна потерям удельной механической энергии. При движении вязкой жидкости из-за трения происходит переход механической энергии в тепло. В силу уравнения неразрывности скорость остается постоянной, а давление убывает вдоль трубы (т.е. давление уменьшается из-за перехода механической энергии в тепло).
Пример 5. На рисунке 3 изображен участок круглой трубы с внезапным расширением от диаметра d1 до диаметра d2=4d1.

Рис. 3
Подсчитаем, где больше скорость и во сколько раз. На основании уравнения неразрывности можно записать:
V1S1=V2S2,
 , окончательно,
, окончательно, 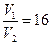 .
.
Таким образом, скорость в трубе больше там, где сечение меньше, а отношение этих скоростей обратно пропорционально квадратам диаметров.
КОНТРОЛЬНЫЕ ВОПРОСЫ К РАЗДЕЛУ «ОБЩИЕ ПОЛОЖЕНИЯ»
1. Что называется расходом?
2. Какую размерность имеют члены уравнения Бернулли?
3. Какое движение называется установившимся?
4. В чем состоит объемный способ определения расхода?
5. Как изменяется кинематический коэффициент вязкости с увеличением температуры?
6. Указать размерность расхода и его наименование в системе СИ.
7. Как изменяется кинематический коэффициент вязкости при понижении температуры?
8. Указать размерность средней скорости потока.
9. Что называется жидкостью?
10. Что называется плотностью?
11. По каким признакам установившееся движение жидкости отличается от неустановившегося, равномерное от неравномерного, напорное от безнапорного?
Задание 1. Измерить расход воды в бытовом водопроводе при полном открытии крана.
Лабораторная работа 1






