Отчетный лист, составленный в виде таблицы, очень удобен как в процессе выполнения, так и по мере оформления работы.
Ниже приведен пример заполненного отчетного листа, а затем все необходимые вычисления.
| № | Физические величины | Ед. измер. | Числовые значения | |
| I | II | |||
| Диаметр трубы d | см | |||
| Площадь поперечного сечения S | см2 | |||
| Количество поступившей в мерный бак воды W бак воды бак,W. | см3 | |||
| Время наполнения, t | с | |||
| Расход воды Q=W / t | см3/с | |||
| Средняя скорость воды в стеклянной трубе V=Q /S. | см/с | 1,4 | ||
| Температура воды Т0 | °C | |||
| Кинематический коэффициент вязкости ν | см2/с | 0,0101 | 0,0101 | |
| Число Рейнольдса Rе = Vd/ ν | - | |||
| Режим движения | - | Турб. | Лам. |
1. Определяем площадь поперечного сечения:
S=πd2 / 4 =7см2.
2. Определяем расход:
Q1=W / t =1000 / 8=125 см3/с;
Q2 =1000 / 102=9,8≈10 см3/с.
3. Определяем среднюю скорость воды:
V1=Q / S =125/7=18 см/с;
V2 =10/7=1,4 см/с.
4. Определяем число Рейнольдса:
Re1=Vd / ν =18·3/0,0101=5346;
Re2 =1.4·3/0,0101=416.
5. Определяем режим движения: 5364>2300 – режим турбулентный;
416 <2300 – режим ламинарный.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как изменяется число Re при повышении температуры воды?
2. Что измеряется в ходе выполнения опыта, а что определяется путем вычислений?
3. Какая скорость называется верхней критической?
4. Укажите значение нижнего критического числа Рейнольдса для круглых напорных труб.
5. Какова размерность числа Rе?
6. Какой режим движения называется ламинарным?
7. Что называется нижним критическим числом Рейнольдса?
8. Какая скорость называется нижней критической?
9. Какой режим движения называется турбулентным?
10. Что называется верхним критическим числом Рейнольдса?
11. Влияет ли температура жидкости на величину критической скорости, при которой меняется режим течения?
ЛИТЕРАТУРА
1. Альтшуль А.Д. Гидравлика и аэродинамика / А.Д. Альтшуль, П.Г. Киселев - М.: Стройиздат, 1975. С. 66-67,147-150.
2. Константинов Н.М. Гидравлика. Гидрология. Гидрометрия / Н.М. Константинов, Н.А. Петров, Л.И. Высоцкий - М.: Стройиздат, 1987. С. 151-156.
Лабораторная работа 2.
ИССЛЕДОВАНИЕ КОЭФФИЦИЕНТА
ГИДРАВЛИЧЕСКОГО ТРЕНИЯ
Твердые границы (стенки труб, например), внутри которых протекает или которые обтекает поток, оказывают на него тормозящее действие. С механической точки зрения, действие твердых поверхностей на поток эквивалентно действию сил, непрерывно распределенных по соприкасающимся с потоком поверхностям. Касательные продольные составляющие этих сил (напряжения трения) создают сопротивление движению потока, называемое сопротивлением трения. Потеря механической энергии потока на преодоление сопротивления трения называется потерей энергии на трение по длине или потерей напора по длине.
Потери напора определяются по формуле Дарси-Вейсбаха:
 , (9)
, (9)
где l – длина трубопровода; d – диаметр трубы; V – средняя скорость; λ – коэффициент гидравлического трения; g – ускорение свободного падения.
В результате экспериментальных исследований было установлено, что коэффициент гидравлического трения λ в общем случае зависит от числа Рейнольдса Re=Vd/ν и относительной шероховатости k/d; он может быть представлен в виде общей функциональной зависимости:
λ=f (Re, k/d),
где k – величина выступов шероховатости стенок трубы; d – диаметр трубы.
Существует пять зон гидравлического сопротивления. Рассмотрим их последовательность при возрастании числа Рейнольдса.
1. Зона вязкого сопротивления (Rе < 2300, ламинарный режим)
При ламинарном режиме движения величина k не влияет на потери напора, и коэффициент λ определяется по формуле:
λ=  . (10)
. (10)
Потери напора в этой зоне пропорциональны скорости в первой степени.
2. Переходная зона
Для чисел Rе в пределах от 2300 до 4500 имеет место переходная зона, характеризующаяся неустойчивостью ламинарного режима.
Для этой зоны Калякиным А.М. и Чесноковой Е.В. была предложена зависимость
λ =  (11)
(11)
Для определения коэффициента λ в этой зоне необходимо число Рейнольдса подставить в эту формулу.
Для определения зоны сопротивления и выбора зависимости для вычисления λ при турбулентном режиме находят значение параметра

3. Зона гладкостенного сопротивления
Увеличение скорости (и числа Rе) приводит к возникновению турбулентного режима движения. В центральной части потока, занимающей почти все сечение трубы, располагается турбулентное ядро. Как показывают эксперименты, около стенок трубы находится ламинарный подслой, его толщина δ зависит от числа Рейнольдса: чем число Rе больше, тем меньше величина δ. В случае, когда толщина ламинарного подслоя δ больше величины выступов шероховатости k, то есть δ > k, стенки называются гидравлически «гладкими», (рисунок 6 а). Зона сопротивления, соответствующая гидравлически «гладким» стенкам, называется зоной гладкостенного сопротивления.
|
|
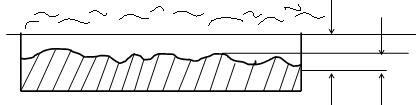
а
|
|
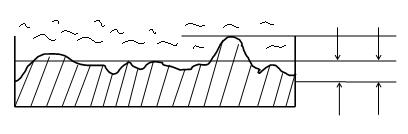
б
|
|
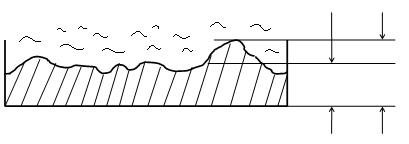
в
Рис. 6
Если
 ,
,
то имеет место гладкостенная зона сопротивления и используется формула Блазиуса
λ =  . (12)
. (12)
4. 3она доквадратичного сопротивления
Увеличение скорости потока V приводит к уменьшению толщины ламинарного подслоя δ, который по толщине становится соизмерим с высотой k выступов шероховатости (рисунок 6 б). Соответствующая зона сопротивления называется зоной доквадратичного сопротивления. Влияние шероховатости стенок трубы на потери растет, и коэффициент λ начинает зависеть от отношения k/d. Показателем того, что имеет место доквадратичная зона, является выполнение неравенства:
 , (13)
, (13)
где kэ – эквивалентная шероховатость (см. зона квадратичного сопротивления).
В этом случае коэффициент λ может быть определен по формуле А.Д. Альтшуля:
 (14)
(14)
5. Зона квадратичного сопротивления
При дальнейшем увеличении числа Re, при развитом турбулентном режиме, когда k >d (рисунок 6 в), имеет место зона квадратичного сопротивления. Влияние числа Re на коэффициент λ в этой зоне исчезает, и λ зависит только от kэ.,/d; поверхности, в этом случае называются «гидравлически шероховатыми». Критерием квадратичной зоны может являться неравенство:
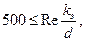 (15)
(15)
коэффициент λ можно определить по формуле Шифринсона:
 (16)
(16)
где kэ – эквивалентная шероховатость, то есть такая однородная равнозернистая шероховатость, которая в квадратичной зоне сопротивления создает такие же потери, как и естественная неоднородная шероховатость. Величина kэ может быть определена опытным путем. Например, по формуле Дарси-Вейсбаха в квадратичной зоне определяется коэффициент λ, затем при известном λ из формулы Шифринсона определяется величина kэ. Значение kэ можно также определить по таблицам в гидравлических справочниках.
Цели работы
1. Определение опытным путем потери напора на трение в трубе и величин коэффициента λ.
2. Установление зоны гидравлического сопротивления.
3. Построение опытной зависимости коэффициента гидравлического трения λ от числа Рейнольдса.
4. Сравнение теоретических и опытных значений коэффициентов
5. Определение величины абсолютной эквивалентной шероховатости стенок трубы.





 k
k
 k
k