2-3 деревом называется дерево, в котором каждый внутренний узел имеет двух или трех сыновей, а длины всех путей от корня в листья совпадают между собой. Поскольку в процессе поиска необходимо делать выбор между тремя сыновьями, в 2-3 дереве каждый внутренний узел дерева хранит не один, а два ключа. Линейно упорядоченное множество S можно представить 2-3 деревом, приписав его элементы листьям дерева с использованием заданного порядка. Каждый внутренний узел v содержит две метки L (v) и M (v), где L (v) - наибольший элемент, приписанный листьям самого левого сына вершины v, M (v) - наибольший элемент, приписанный листьям второго сына этой вершины. Используя эти метки для поиска, легко решить задачу НАЙТИ за время пропорциональное высоте дерева (O (log(n))). 2-3 деревья служат хорошей структурой данных для АТД со следующим набором операций:
1. ВСТАВИТЬ, УДАЛИТЬ, НАЙТИ
2. ВСТАВИТЬ, УДАЛИТЬ, НАЙТИ ЭЛЕМЕНТ С МИНИМАЛЬНЫМ
ЗНАЧЕНИЕМ КЛЮЧА
3. ВСТАВИТЬ, УДАЛИТЬ, ОБЪЕДИНИТЬ, НАЙТИ С МИНИМАЛЬНЫМ
ЗНАЧЕНИЕМ КЛЮЧА
4. ВСТАВИТЬ, УДАЛИТЬ, НАЙТИ, СЦЕПИТЬ, РАСЦЕПИТЬ
Как уже упоминалось выше, АТД с набором операций из множества 1 называется
Словарем, из множества 2 – Очередью с приоритетами, 3 – Сливаемым деревом, 4 –
Сцепляемой очередью.
2-3 деревья позволяют эффективно выполнять последовательности операций из любого набора перечисленных операций. Единственная несовместимость состоит в том, что операция ОБЪЕДИНИТЬ приводит к неупорядоченному множеству, а операции СЦЕПИТЬ, РАСЦЕПИТЬ предполагают наличие порядка.
Словари и очереди с приоритетами. Рассмотрим реализацию операции ВСТАВИТЬ в 2-3 дерево. Сначала поиском по дереву определяется место для нового элемента a в последовательности меток листьев дерева. Для этого ищут узел f дерева, имеющий двух или трех сыновей, к листьям которог необходимо приписать a. Если у узла f два сына, то a становится третьим сыном, причем a вставляется с учетом отношения линейного порядка на листьях дерева. В зависимости от позиции элемента a последовательности сыновей вершины f, производится коррекция ее меток L (f) и M (f) таким образом, чтобы они отражали порядок следования сыновей вершины f. Далее с учетом этой информации необходимо рекурсивно подправить метки вершин (предков узла f), лежащих на пути от вершины f к корню дерева. Если после добавления вершины a, число листьев вершины f становится равным 4, то вершину f расщепляют на два узла f и g с общим отцом, оставляя двух левых сыновей вершине f, а двух правых относя вершине g. Поскольку вершины f и g, имеют общего отца q, проверяют число сыновей у вершины q. Если q имеет не более трех сыновей, процесс расщепления завершается, если числосыновей равно 4, то вершина q,аналогично f расщепляется на две, каждая из которых имеет двух сыновей, и процесс продолжается по направлению к корню дерева. Как и в первом случае в процессе
приведения дерева к виду 2-3 дерева, необходимо откорректировать метки вершин на пути от вершины f к корню. Общее время операции по вставке элемента в n –элементное множество равно O (log n) шагов. Процесс удаления вершины из дерева является обратным к операции вставки. Пусть удаляемый элемент a принадлежит листу z. Рассмотрим три случая: 1. Если z является корнем дерева, то он удаляется, и мы получаем пустое дерево. 2. Если z имеет двух братьев, то z удаляется, и далее производится корректировка меток вершин, лежащих на пути от отца вершины z до корня дерева. 3. Если z сын узла f, имеющего двух сыновей s и z, то возможно два варианта продолжения: a) f - корень, удаляем z и f, корнем дерева становится s. b) f - не корень. Если f имеет слева от себя брата g 28, то подсчитывается число сыновей вершины g. Если у g два сына, делаем узел s самым правым сыном вершины g, удаляем z и рекурсивно вызываем процедуру удаления узла f. Если у g три сына, то самого правого сына делаем левым сыном узла f, и удаляем z. Далее проводится корректировка меток
вершин, лежащих на пути от g (возможно и f) до корня дерева.
Продолжение 25
Показано [2], что операция удалить элемент из множества, содержащего n элементов, также занимает O (log n) времени. Таким образом, для словаря 2-3 дерево представляет структуру, позволяющую обеспечить выполнение последовательности из n операций ВСТАВИТЬ, УДАЛИТЬ, НАЙТИ за O (n log n) шагов. Рассмотрим одно из возможных представлений в виде 2-3 дерева уже знакомого нам
множества чисел {6,7,9,10,11,12,13,15,18,21,23,30}

Проиллюстрируем вставку и удаление элемента на следующих примерах. Добавляя элемент 5, получим

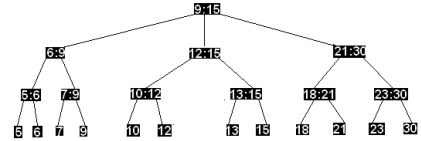
Вершина (6:7) содержит 4 сына и должна быть расщеплена на две вершины (5:6) и (7:9), каждая из которых имеет отцом вершину (9:11). Далее поднимаясь на один уровень вверх, исследуем вершину (9:11). Поскольку эта вершина содержит 4 сына, она также расщепляется на две вершины. Исследование вершины верхнего уровня (15:30) показывает, что она удовлетворяет условиям определения 2-3 дерева. И хотя на данном шаге процесс корректировки структуры дерева может быть прерван, процесс корректировки меток продолжается до корня дерева. Результат построения показан на рисунке ниже:

Из получившейся структуры удалим вершину 11. Поскольку после удаления вершина(10:11) имеет единственного сына, то второго сына заимствуем от вершины (12:13) с корректировкой соответствующих меток. Далее необходимо откорректировать метки вершин, находящихся на пути от отца вершин (10:11) и (12:13) до корня дерева.
Что касается очередей с приоритетами, то выполнение операции МИНИМУМ требует O (log n) шагов(минимальный элемент является крайним слева в упорядоченном списке листьев).Следовательно,2-3 деревья служат для реализации АТД Очередь с приоритетами с производительностью O (n log n), где n общее число запросов.






