Балансировки.
Сбалансированные деревья поиска (balanced search tree). Верхнюю оценку в худшем для времени поиска получаем O(log(n)), если удается поддерживать сбалансированную структуру дерева поиска – не менее двух сыновей (почти) у каждой вершины и примерно одинаковая высота поддеревьев у каждого сына.
На сегодняшний день разработано несколько методов перестройки деревьев поиска, которые позволяют поддерживать сбалансированную структуру дерева поиска с приемлемыми расходами по времени, так чтобы общее время в худшем для операций поиска, вставки, удаления и min (АТД «Множество», «Словарь» и «Очередь с приоритетом») сохранялось O(log(n)). Балансировку структуры дерева можно проводить и по высоте, и по объему (весу) поддеревьев. Для бинарных деревьев известны методы балансировки – АВЛ-деревья, красно-черные деревья (RB-tree) и их вариации. Б-деревья — это один из видов сбалансированных деревьев, обеспечивающих эффективное хранение информации на магнитных дисках и других внешних устройствах с прямым доступом. Б-деревья являются обобщением 2-3 деревьев, разница в том, что в Б- дереве каждый внутренний узел может иметь много детей, на практике до тысячи, в зависимости от характеристик используемого диска. Благодаря этому можно значительно уменьшить высоту дерева и понизить константу в оценке O (log n) времени поиска элемента. В основном Б-деревья служат для реализации доступа к данным файла по ключу поиска. Для этого создается (и поддерживается) индексный файл, который фактически является реализацией АТД словарь. Специфическая структура данных – Splay-дерево. Это бинарное дерево поиска, но при этом не поддерживается явного баланса, оно может оказаться разбалансированным в определенном (традиционном) смысле. Вместо этого после выполнения каждой операции, типовой для бинарных поисковых деревьев, осуществляется перестройка (сохраняющая определяющие свойства поискового дерева) с целью «подтянуть» вершину этой операции (для операции удаления - её родителя), поближе к корню, что ускорит её нахождение в будущем. Для такого представления вышеупомянутые операции с множествами (и некоторый набор дополнительных операций) имеют время работы O(log(n)), но амортизированное. Перестройка проводится с помощь трех Splay-операций: § Zig: Если родитель вершины x является корнем:

§ Zig-Zig: Если родитель вершины x не является конем, но x и его родитель либо оба левые либо оба правые сыновья:

§ Zig-Zag: Если родитель вершины x не является конем, но x – левый сын, а его родитель – правый сын:

Продолжение 23
Возможности организовать балансировку расширяются, если допускать изменение количества сыновей вершины в фиксированном диапазоне [k,m]. К таким методам балансировки относятся 2-3-деревья, В деревья и их вариации. Сильно ветвящиеся В-деревья представляют особый интерес при работе с данными, хранящимися во внешней памяти. Существует множество других операций над сбалансированными деревьями, которые поддерживают их сбалансированность. Сбалансированные деревья используются и для представления последовательностей таким образом, что можно будет быстро вставлять элементы в последовательность, преодолевая трудности, которые связаны с последовательным расположением элементов (в массиве), и обеспечивая при этом произвольный доступ к элементам последовательности, т. е. преодолевая сложности связанного размещения элементов. При этом такие представления позволяют эффективно реализовать операции сцепить (конкатенация) и расцепить для последовательностей. Исследуются и известны расширения выше отмеченных структур данных предназначенные для применения в различных предметных областях, естественно имеющих свою специфику интерпретации данных. Например, расширение красно- черных деревьев для работы с ключами вида интервал вещественных чисел, которое представляет прямой интерес в задачах вычислительной геометрии.
Балансировка
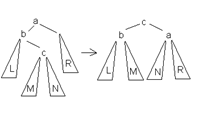
1.Малое левое вращение

Данное вращение используется тогда, когда (высота b-поддерева - высота L) = 2 и высота С <= высота R. 2.Большое левое вращение

3.Малое правое вращение

Данное вращение используется тогда, когда (высота b-поддерева — высота R) = 2 и высота С <= высота L.
4.Большое правое вращение