Улучшенные методы сортировки (Шелла, Сортдеревом).

Метод Шелла. В 1959 году Д.Шелл предложил алгоритм, который можно рассматривать

как усовершенствование сортировки простыми включениями. Как уже упоминалось,

алгоритм с простыми включениями достаточно эффективно работает на частично

упорядоченных последовательностях. Поэтому, если на первых шагах производить

упорядочивание далеко отстоящих элементов, и с каждым проходом сокращать

расстояние между элементами, то можно улучшить сложностные показатели метода

простых вставок. В варианте Шелла на i -м шаге алгоритма текущая последовательность

разбивается на подмножества элементов, которые отстоят друг от друга в исходной

последовательности на расстоянии hi, с последующей сортировкой элементов в каждом

множестве. Числа hi убывают от шага к шагу в определенном порядке (например, может

быть 2^ t, 2^ t -1,…,2,1), на последнем шаге сортируется вся последовательность (другое

название алгоритма Шелла - сортировка включением с уменьшающимся расстоянием),

однако эта операция производится на достаточно хорошо к этому моменту упорядоченной

последовательности. Каждый проход алгоритма использует результаты предыдущих

проходов. Основная идея состоит в перемешивании достаточно далеко расположенных

друг от друга элементов с последующим уменьшением этого расстояния.

Проиллюстрируем метод Шелла для нашего примера с шагами h1=6 h2=3, h3=2, h4=1

Фактически метод Шелла на каждом шаге разбивает последовательность на

подпоследовательности, локально упорядочивая каждую из них. Далее набор

подпоследовательностей трактуется как единая последовательность, и процесс

повторяется с новым разбиением. Оценка эффективности времени работы этого алгоритма

достаточно сложна, она существенно зависит от выбора последовательности чисел

h1, h2,..., h t. Кнут [14] показал, что достаточно эффективная реализация получается при

следующей зависимости: h(i-1)=3h(i)+1, h(t)=1, t=(log₃n) -1. Наилучшая

последовательность приращений неизвестна. Однако доказано, что числа этой

последовательности не должны быть кратны друг другу⁴³. Более подробный анализ

метода Шелла приведен в [14]. Показано, при определенном выборе последовательности

h(i) сложность алгоритма может оцениваться как O (n log² n)» O (n ^1,2 ). При реализации

алгоритма для хранения последовательности используется массив. Эффективность этого

алгоритма объясняется тем, что при каждом проходе используется относительно

небольшое число элементов или элементы массива уже находятся в относительном

порядке, а упорядоченность массива увеличивается при каждом новом просмотре данных.

Алгоритм сортировки с помощью кучи (пирамидальная сортировка). Рассмотрим

алгоритм, улучшающий метод, связанный с простым выбором. Предположим, что при

обновлении R2 алгоритм передает из R1 максимальный элемент (случай сортировки по

неубыванию). Другими словами имеем абстрактный тип данных множество с операциями

поиска максимального элемента и его удаления. АТД с такими операциями хорошо

известен и называется очередью с приоритетами. Поскольку последовательная структура

реализации такого типа данных (массив, линейный список) дает линейную оценку для

реализации операции поиска максимального элемента, возникает вопрос об

использовании древообразных структур, поддерживающих требуемое отношение порядка

между элементами и учитывающих свойство транзитивности этого отношения. Такая

структура существует и называется двоичной кучей. В силу свойства транзитивности при

поиске максимального элемента отпадает необходимость попарного его сравнения с

каждым элементом из R1. Негативной стороной такого подхода является необходимость

поддержки основных свойств структуры при изменении R1. Покажем, что можно за O (n)

шагов построить и, в дальнейшем, поддерживать структуру данных задающих частичный

порядок на элементах множества R 1.

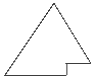
Двоичной кучей (пирамидой) называется массив, элементы которого обладают

определенными свойствами. Формулировку этих свойств удобно проводить на языке

бинарных деревьев. Рассмотрим бинарное дерево, каждая вершина которого

соответствует некоторому элементу массива. Если вершина соответствует элементу ai, то отец этой вершины хранит информацию об элементе a_i/2, а дети соответствуют

элементам массива с индексами 2 i и 2 i +1. Такое дерево напоминает пирамиду, вид этого

дерева показан на рисунке

Понятно, что любой начальный отрезок массива также обладает такими свойствами.

Основное свойство, которое должно поддерживаться кучей заключается в следующем:

значение элемента приписанному отцу вершины ai не меньше значения, приписанного

самой вершине (a отец (I) >= a (i)). Очевидно, куча, для которой выполняется основное

свойство, задает частичный порядок на элементах массива (а потому её ещё называют

сортирующим деревом). Процедура построения отношения частичного порядка, является

рекурсивной. Пусть отношение частичного порядка выполняется для вершин поддеревьев

D1 и D2.

 

Поскольку на каждом из деревьев D1 и D2 выполняется отношение частичного порядка,

то это отношение может быть нарушено только для корня дерева. Сравнивая элемент a с

корнями деревьев D1 и D2 и, в случае нарушения порядка, обменивая a со значением

одного из корней, получаем ситуацию, когда отношение частичного порядка может не

выполняться для одного из деревьев D1 или D2. Продолжая рекурсивно этот процесс,

можно добиться того, что для всех поддеревьев выполняется отношение частичного

порядка. Поскольку, необходимо просмотреть n / 2 поддеревьев, и построение

частичного порядка для каждого из них занимает не более log n шагов получаем верхнюю

оценку на время построения кучи O (n log n). Более точный подсчет с учетом высоты, уже

построенной части пирамиды дает оценку O (n).

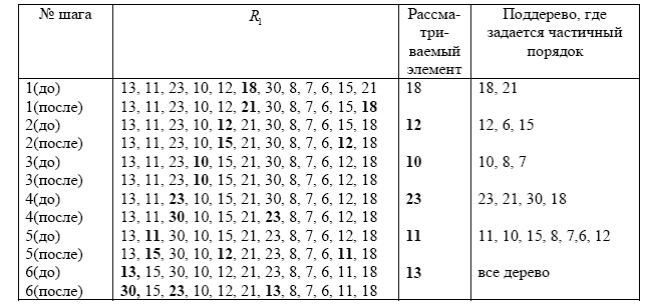
Рассмотрим пример построения кучи для последовательности 13, 11, 23, 10, 12, 18, 30,

8, 7, 6, 15, 21. Строка № (до) характеризует состояние массива до операции построения

частичного порядка на поддереве, корень которого выделен жирным шрифтом. Строка №

(после) характеризует массив после построения частичного порядка на соответствующем

поддереве. В этой строке выделены элементы, которые участвуют (посредством обмена) в

построении требуемого порядка.

 

Ниже на рисунке графически проиллюстрированы шаги по построению сортирующего

дерева для нашего примера

 

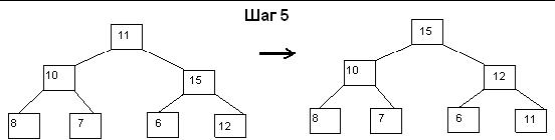
Слева от стрелки нарисовано состояние поддерева до выполнения шага, а справа – после.

Поскольку максимальный элемент массива приписан корню дерева, то поиск и извлечение

максимального элемента занимает O (1) шагов. Поскольку в процессе работы алгоритма

множество R1 изменяется (удаляются максимальные элементы), то необходима

процедура, позволяющая поддерживать свойства сортирующего дерева при изменении R 1.

Можно показать, что время работы такой процедуры связано с высотой дерева и

составляет O (log n). Поскольку сортирующее дерево кодирует массив с фиксированными

связями между определенными индексами элементов, все операции на дереве легко

моделируются на линейном массиве. Основное свойство сортирующего дерева для

массива записывается с использованием неравенств: a(i)=<a(2i) и a(i)=<a(2i+1), i=1,2,…,n/2

Алгоритм сортировки с помощью двоичной кучи состоит из следующих шагов:

1. Построение сортирующего дерева, сложность - O (n).

2. Для каждого начального отрезка массива длины i (i = n, n -1,...,1) найти

максимальный элемент, поменять этот элемент с последним элементом начального

отрезка массива, уменьшить число элементов 1 и переставляя элементы

восстановить основное свойство кучи. Сложность - O (n log n)

Рассмотрим сортировку на нашем примере. В строках таблицы приведены состояния

последовательностей R1 и R2 на момент обновления R2 (после) и приведения

последовательности R1 к основному свойству кучи (до). Элементы, участвующие в

обменах на соответствующих шагах выделены жирным шрифтом.