Обработка результатов измерений
Доверительные границы погрешностей значений nn, nx, nU вычисляют по алгоритму прямых измерений с доверительной вероятностью Р = 0,95. Доверительный интервал для неизвестной величины ЭДС определяют из формулы
.
Внутреннее сопротивление элемента определяют при трех различных значениях R1. Каждый раз определяют 
из пяти измерений, находят среднее значение 
и доверительные границы его погрешности по алгоритму прямых измерений.
Содержание отчёта
Отчет должен содержать:
1. Чертеж измерительной схемы.
2. Пять значений величин nn, n x, nU.
3. Расчеты по алгоритму прямых измерений их средних значений и доверительных границ погрешности.
4. Расчет внутреннего сопротивления r 0 элемента Ех и доверительные границы его погрешности.
Контрольные вопросы
s В чем заключается сущность работы схемы компенсации ЭДС?
s Как определяется внутреннее сопротивление элемента? (Выведите формулу).
s Для каких целей могут быть использованы компенсационные схемы?
Лабораторная работа 33
ОПРЕДЕЛЕНИЕ ЕМКОСТЕЙ КОНДЕНСАТОРОВ И ЭДС ГАЛЬВАНИЧЕСКИХ ЭЛЕМЕНТОВ ПРИ ПОМОЩИ ГАЛЬВАНОМЕТРА
Задачи работы
1. Градуировка гальванометра.
2. Определение емкости конденсаторов, а также систем конденсаторов.
3. Определение ЭДС гальванических элементов.
Физическое обоснование эксперимента
Если сообщить проводнику электрический заряд, то его потенциал относительно какой-либо точки пространства будет возрастать пропорционально заряду:
 ,
| (33.1) |
где q – заряд, φ – потенциал. Коэффициент пропорциональности C называется электрической емкостью (электроемкостью) или просто емкостью проводника. Емкость характеризует способность проводника накапливать электрические заряды. Иными словами, емкостью C называется отношение сообщённого заряда q к возникающему в результате этого потенциалу φ:
 ,
| (33.2) |
т. е. численно емкость равна заряду, который необходимо сообщить уединенному проводнику для изменения его потенциала на единицу.
Единицей электроемкости проводников в системе СИ является фарад [1] (устаревшее название – фарада) (Ф, F) – емкость проводника, потенциал которого изменяется на 1 вольт при сообщении проводнику заряда в 1 кулон: 1 Ф = 1 
.
Следует иметь в виду, что фарад – очень большая величина (емкость шара с радиусом, равном земному, имеет емкость 7·10–4 Ф. Чаще применяются дольные единицы: микрофарад (мкФ, mF), равный 10–6 Ф, нанофарад (нФ, nF), равный 10–9 Ф и пикофарад (пФ, pF), равный 10–12 Ф.
Емкость определяется геометрическими размерами проводника, его формой и электрическими свойствами окружающей среды (ее диэлектрической проницаемостью) и не зависит от материала проводника. Наличие вблизи проводника других тел изменяет его емкость. Электрическая емкость изолированного проводника мала.
Электрический конденсатор – устройство из нескольких проводников, разделенных слоем диэлектрика.
Простейший конденсатор, состоящий из двух плоских параллельных пластин одинаковой площади (обкладок), разделенных тонким слоем диэлектрика, называется плоским конденсатором (рис. 33.1).
Рис. 33.1. Плоский конденсатор.
Емкость такого конденсатора С =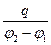 
определяется его геометрическими размерами и свойствами диэлектрика. В конденсаторе электрическое поле сосредоточено в основном между его обкладками, поэтому емкость конденсатора практически не зависит от окружающих тел и может достигать больших величин при малых размерах конденсатора. Если на единице поверхности обкладок имеется заряд σ и диэлектриком является вакуум, то полное напряжение между обкладками равно:
 ,
| (33.3) |
где U – напряжение между пластинами, d – расстояние между пластинами. Если площадь каждой пластины равна S, то полный заряд пластины есть q = σ S. Поэтому:
 .
| (33.4) |
Если диэлектриком является не вакуум, а вещество с диэлектрической проницаемостью e, заполняющее все пространство, где имеется электрическое поле (пространство между обкладками), то емкость будет в e раз больше:
 .
| (33.5) |
Электрические конденсаторы часто включаются группами (в виде батарей). При присоединении нескольких конденсаторов друг к другу различают параллельное (рис. 33.2) и последовательное (рис. 33.3) их соединения.
Рис. 33.2. Параллельное соединение конденсаторов: C ОБЩ = С 1 + С 2 + C 3 + … + Сn.
При параллельном соединении конденсаторов (рис. 33.2) одна из пластин каждого конденсатора имеет один и тот же потенциал φ1, а другая φ2. На пластинах каждого конденсатора находится заряд qi (i = 1, 2, 3,..., n), так что суммарный заряд всех конденсаторов равняется:
 .
| (33.6) |
Отсюда следует:
 ,  .
| (33.7) |
Рис. 33.3. Последовательное соединение конденсаторов: 
.
При последовательном соединении конденсаторов (рис. 33.3) под влиянием приложенной разности потенциалов их пластины электризуются так, что на них появляются равные, но противоположные по знаку заряды q. Разности потенциалов пластин каждого конденсатора суммируются (пусть n = 3):
 .
| (33.8) |
Следовательно:
 .
| (33.9) |
Метод исследования и описание установки
В данной работе в качестве измерительного прибора используется баллистический гальванометр. Баллистический гальванометр применяется для измерений количества электричества и представляет собой магнитоэлектрический гальванометр с искусственно увеличенным моментом инерции подвижного индикатора (период собственных колебаний T0 ≥ 15 c), включаемый последовательно в цепь, по которой протекает импульсный ток. Если длительность импульса тока много меньше T0, то первое наибольшее отклонение индикатора l m (баллистический отброс) после протекания тока пропорционально количеству электричества q, протекающего через рамку баллистического гальванометра:
| q = К Г l m, | (33.10) |
где K Г – баллистическая постоянная по заряду или просто постоянная гальванометра, l m – баллистический отброс.
Баллистическая чувствительность по заряду (чувствительность к протекающему через баллистический гальванометр заряду) и обратная ей величина (баллистическая постоянная K Г) зависят от сопротивления внешней электрической цепи, на которую замкнут баллистический гальванометр во время измерений. Поэтому баллистический гальванометр градуируют при том же внешнем сопротивлении, при котором будут выполняться измерения.
Если известна баллистическая постоянная гальванометра, то по баллистическому отбросу можно определить заряд q, прошедший через гальванометр. В работе через гальванометр пропускается заряд конденсатора С (Рис.33.4), который будет определяться емкостью С включенного в схему конденсатора и электродвижущей силой элемента питания Е. В соответствии с формулой 33.4 q = C E. Таким образом, если известна ЭДС элемента, то можно определить емкость и наоборот.
Работа выполняется на одной из трех установок (электрическая схема, состоящая из гальванометра (обычно М195/3 или М197/2), нормального элемента Вестона (Ε0 = 1,0183 В), магазина емкости (обычно Р5025 или Р523), двух неизвестных конденсаторов и переключателя), а также двух гальванических элементов с неизвестными ЭДС (в состав установки не входят – получите у лаборанта).
В качестве С в данную схему может быть включен либо магазин емкости либо исследуемые конденсаторы, в качестве Е - либо нормальный элемент либо исследуемый элемент.
Рис. 33.4. Рабочая схема.
Порядок выполнения работы
Градуировка гальванометра
1. Собрать электрическую схему, изображенную на рис. 33.3. В качестве конденсатора C включить в схему магазин емкости C0, а в качестве источника ЭДС – элемент Вестона E0.
2. Установить на магазине емкости C0 некое значение емкости (например, 0,1 мкФ).
3. Ключом К1 замкнуть конденсатор C0 на нормальный элемент E0, при этом конденсатор емкостью C 0 зарядится до напряжения, равного E0.
4. С помощью ключа К1 быстро переключить конденсатор C0 на гальванометр Г, при этом конденсатор начнет разряжаться через гальванометр, т. е. через него потечет заряд q = С 0E0. Так как гальванометр в нормальном состоянии все время закорочен кнопкой К2, то для получения отброса необходимо непосредственно во время переключения ключа К1 нажать кнопку К2. Отпускать ее следует сразу после прохождения указателем начального положения.
5. Записать максимальный отброс l m, наблюдаемый на шкале гальванометра.
6. Проградуировать гальванометр, последовательно повторяя пункты 2-5 для различных значений емкости C 0 (например, через 0,1 мкФ).
