Задачи работы
1. Определение сопротивления проводников с помощью моста постоянного тока.
2. Расчет удельного сопротивления проводников.
Физическое обоснование эксперимента
Электрический ток в металлах – проводниках 1-го рода – обусловлен направленным (упорядоченным) движением электронов под действием приложенного электрического поля. Электроны в металлах считаются «свободными» из-за сравнительно слабой связи с ионами кристаллической решетки, внутри которой они могут свободно перемещаться.
Для создания и поддержания упорядоченного движения заряженных частиц необходимо электрическое поле. Если внутри проводника имеется электрическое поле, то между концами проводника существует разность потенциалов ∆ φ, именуемая также напряжением.
Заряд, перенесенный в единицу времени, служит основной количественной характеристикой тока, называемой силой тока.
Сила тока I, текущего по однородному металлическому проводнику, согласно закону Ома пропорциональна напряжению U на проводнике (разности потенциалов электрического поля), приложенному к концам проводника:
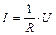 , (31.1)
, (31.1)
где 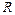 – электрическое сопротивление проводника.
– электрическое сопротивление проводника.
Величина сопротивления зависит от геометрической формы и размеров проводника, а также от свойств материала, из которого он сделан. Для длинного проводника с круглым сечением
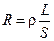 , (31.2)
, (31.2)
где 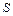 – площадь его поперечного сечения, а ρ – коэффициент, зависящий от свойств материала, называемый удельным электрическим сопротивлением,
– площадь его поперечного сечения, а ρ – коэффициент, зависящий от свойств материала, называемый удельным электрическим сопротивлением, 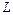 – длина проводника. При
– длина проводника. При 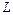 = 1 м и
= 1 м и 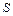 = 1 м2, R = ρ, т. е. коэффициент ρ численно равен сопротивлению проводника единичной длины и единичного поперечного сечения. В системе СИ ρ измеряется в ом-метрах (Ом·м). Величина σ= 1/ρ называется удельной электрической проводимостью и выражается в сименсах на метр (См/м).
= 1 м2, R = ρ, т. е. коэффициент ρ численно равен сопротивлению проводника единичной длины и единичного поперечного сечения. В системе СИ ρ измеряется в ом-метрах (Ом·м). Величина σ= 1/ρ называется удельной электрической проводимостью и выражается в сименсах на метр (См/м).
Какова физическая природа электрического сопротивления R?
Согласно классической теории электроны проводимости в металлах ведут себя как частицы идеального газа. Двигаясь упорядоченно, они взаимодействуют (упруго сталкиваются) с положительными ионами в узлах кристаллической решетки, и изменяют направленность своего движения (рассеиваются).
Однако классическая теория натолкнулась на трудности в вопросе о теплоемкости электронного газа. Кроме того, экспериментально наблюдаемая пропорциональность удельного сопротивления ρ температуре также не могла быть объяснена с классической точки зрения.
Эти проблемы были преодолены в квантовой механике, которая рассматривает движение электрона как распространение волны. Электронные волны рассеиваются на неоднородностях, всегда существующих в кристаллической решетке. В случае идеальной решетки неоднородности, рассеивающие волны, связаны лишь с тепловым движением (колебаниями) решетки, что ведет к пропорциональности удельного сопротивления ρ температуре кристалла t. При наличии примесей в кристаллической решетке имеются неоднородности, не зависящие от температуры, поэтому связь удельного сопротивления ρ с температурой принимает вид:
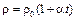 ,
,
где ρ0 – значение удельного сопротивления металла при температуре t → 00 C, 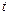 – температура, α – температурный коэффициент сопротивления.
– температура, α – температурный коэффициент сопротивления.
Для большинства металлов при температурах, близких к комнатной, ρ изменяется пропорционально температуре. При низких температурах наблюдается отступление от этой закономерности.
Если известно сопротивление R однородного цилиндрического проводника диаметром d и длиной L, то расчет удельного сопротивления ρ производится по формуле:
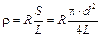 , (31.3)
, (31.3)
Существуют несколько способов измерения R:
а) прямое измерение омметром;
б) косвенное измерение с помощью других электроизмерительных приборов, например, вольтметра и амперметра;
в) измерение с помощью моста постоянного тока, называемого также мостом Уитстона. Мостовой метод является наиболее точным, так как позволяет исключить погрешности, вносимые омметром и иными приборами. Подробнее о погрешностях электроизмерительных приборов можно прочитать в разделе «Электроизмерительные приборы».
Измерение сопротивления проводников с помощью моста постоянного тока
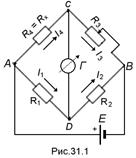 Рассмотрим принципиальную схему четырехплечевого моста постоянного тока. Четыре сопротивления (четыре плеча) R 1, R 2, R 3, R 4, соединены в четырехугольник ADBC (рис. 31.1). Сопротивление R 4 = RX является измеряемым, остальные три известны, причем, по крайней мере, одно из них (в данном случае R 3) является регулируемым. В одну из диагоналей моста AB включен источник питания, во вторую – магнитоэлектрический нулевой индикатор – обычно гальванометр Г. Гальванометр является высокочувствительным прибором, предназначенным для измерений очень малых токов (менее 10–6 А).
Рассмотрим принципиальную схему четырехплечевого моста постоянного тока. Четыре сопротивления (четыре плеча) R 1, R 2, R 3, R 4, соединены в четырехугольник ADBC (рис. 31.1). Сопротивление R 4 = RX является измеряемым, остальные три известны, причем, по крайней мере, одно из них (в данном случае R 3) является регулируемым. В одну из диагоналей моста AB включен источник питания, во вторую – магнитоэлектрический нулевой индикатор – обычно гальванометр Г. Гальванометр является высокочувствительным прибором, предназначенным для измерений очень малых токов (менее 10–6 А).
Меняя величину регулируемого сопротивления, можно добиться такого состояния схемы, при котором напряжение (разность потенциалов) между точками C и D, и, следовательно, ток в гальванометре Г равны нулю. Это состояние называют состоянием равновесия моста (мост сбалансирован).
Состояние равновесия наступает только при определенном соотношении плеч моста – сопротивлений R 1, R 2, R 3, R 4.
Обозначим I 1, I 2, I 3, I 4 – силу токов, текущих по соответствующим плечам, ток через гальванометр – I Г, а потенциалы в точках A, B, C, D – V A, V B, V C, V D. Если мост сбалансирован, то I Г = 0. Это возможно при условии, что потенциалы в точках C и D одинаковы. Значит, в случае баланса моста имеем:
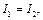
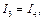 φС = φD. (31.4)
φС = φD. (31.4)
По закону Ома имеем:
I 1 = (φA – φD)/ R 1, I 2 = (φD – φB) /R 2,
I 4 = (φA – φC)/ R 4, I 3 = (φC – φВ)/ R 3,
Разделив I 4 на I 1, а I 3 на I 2, с учетом равенства (31.4) получим:
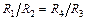 . (31.5)
. (31.5)
Таким образом, если ток в гальванометре отсутствует, то неизвестное сопротивление RX = R 4 можно выразить через три другие сопротивления
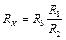 , (31.6)
, (31.6)
где R 3 – сопротивление в плече сравнения, R 1 и R 2 – сопротивления плечей отношения. Из (31.6) видно, что измерение сопротивления RX сводится к регулировке плеча сравнения R 3 при постоянном отношении 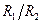 , (либо к регулированию отношения
, (либо к регулированию отношения 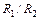 при постоянном значении R 3) до исчезновения тока I Г в гальванометре. При этом RX является сопротивлением всего плеча моста, ограниченного узлами A и C, включая сопротивления соединительных проводов и сопротивления всех контактов между этими точками. Если измеряемое сопротивление RX много больше сопротивления проводов и контактов (которые трудно сделать меньше нескольких тысячных долей Ома), то измерение RX может быть произведено с достаточно высокой точностью. Однако, если RX мало (меньше 1 Ом), то погрешность определения RX велика, и надо применять более сложные мостовые схемы. При измерении больших сопротивлений (больше 100 кОм) погрешности возможны из-за токов утечки, которые могут появляться вследствие соизмеримости сопротивлений изоляции моста и измеряемого сопротивления. Поэтому большие сопротивления измеряют с помощью других методов. Четырехплечевой мост постоянного тока обычно применяется для измерения сопротивлений в пределах от 1 Ом до 100 кОм.
при постоянном значении R 3) до исчезновения тока I Г в гальванометре. При этом RX является сопротивлением всего плеча моста, ограниченного узлами A и C, включая сопротивления соединительных проводов и сопротивления всех контактов между этими точками. Если измеряемое сопротивление RX много больше сопротивления проводов и контактов (которые трудно сделать меньше нескольких тысячных долей Ома), то измерение RX может быть произведено с достаточно высокой точностью. Однако, если RX мало (меньше 1 Ом), то погрешность определения RX велика, и надо применять более сложные мостовые схемы. При измерении больших сопротивлений (больше 100 кОм) погрешности возможны из-за токов утечки, которые могут появляться вследствие соизмеримости сопротивлений изоляции моста и измеряемого сопротивления. Поэтому большие сопротивления измеряют с помощью других методов. Четырехплечевой мост постоянного тока обычно применяется для измерения сопротивлений в пределах от 1 Ом до 100 кОм.
Метод измерений сопротивлений с помощью моста – это метод сравнения или нулевой метод: неизвестное сопротивление сравнивается с известным, а гальванометр служит индикатором отсутствия тока в диагонали моста. Следовательно, точность измерения обусловлена точностью изготовления известных сопротивлений и чувствительностью гальванометра (чувствительностью моста).
Можно показать, что чувствительность моста максимальна, когда 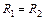 , т. к. при этом погрешность измерения RX – минимальна.
, т. к. при этом погрешность измерения RX – минимальна.
Описание экспериментальной установки
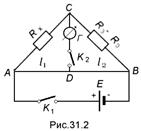
В работе используется четырехплечевой реохордный мост (рис. 31.2). В нем плечи отношения  и
и 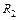 выполнены в виде реохорда ADB – однородного калиброванного провода неизменного сечения, по которому перемещается контакт D, являющийся одним из узлов моста. Длина реохорда l = 1 м, и натянут он вдоль миллиметровой линейки. Скользящий контакт D (ползунок) с выключателем К2 может быть снабжен нониусом. Гальванометр Г включен в диагональ моста CD. Источник питания Ε и ключ К1 включены в диагональ AB. RX – измеряемое сопротивление, R 3 = R 0 – эталонное сопротивление (в виде магазина сопротивлений). Пока мост не сбалансирован ключ К2 замыкается лишь на очень короткое время во избежание длительного протекания через него больших токов!
выполнены в виде реохорда ADB – однородного калиброванного провода неизменного сечения, по которому перемещается контакт D, являющийся одним из узлов моста. Длина реохорда l = 1 м, и натянут он вдоль миллиметровой линейки. Скользящий контакт D (ползунок) с выключателем К2 может быть снабжен нониусом. Гальванометр Г включен в диагональ моста CD. Источник питания Ε и ключ К1 включены в диагональ AB. RX – измеряемое сопротивление, R 3 = R 0 – эталонное сопротивление (в виде магазина сопротивлений). Пока мост не сбалансирован ключ К2 замыкается лишь на очень короткое время во избежание длительного протекания через него больших токов!
Для реохорда отношение R 1/ R 2 равно отношению длин соответствующих отрезков проволоки l 1 и l 2 = l – l 1:
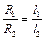 и
и 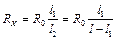 . (31.7)
. (31.7)
Исследуемые проводники RX натянуты на деревянном столбике и их концы выведены на клеммы, длина проволок 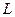 указана на основании столбика.
указана на основании столбика.
Порядок выполнения работы
1. Собрать схему (рис. 31.2).
2. После проверки схемы моста замкнуть ключ К1, установить ползунок D на середине реохорда и, подбирая различные значения R 0 на магазине сопротивлений, добиться того, чтобы ток через гальванометр Г был минимальным.
Подбирать R 0 нужно методом «ножниц», который основывается на том, что при 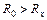 стрелка гальванометра отклоняется в одну сторону, при
стрелка гальванометра отклоняется в одну сторону, при 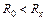 – в другую. Метод заключается в следующем. Установить на магазине сопротивлений заведомо малое сопротивление (R 0 = 0 Ом). Замкнуть ключ К2. Заметить, в какую сторону отклоняется стрелка гальванометра. Разомкнуть К2. Выставить заведомо большое сопротивление (по указанию преподавателя). Убедиться, что стрелка гальванометра отклоняется в другую сторону. Задать промежуточное значение плеча сравнения (например, R 0 = 5 Ом). По отклонению стрелки определить является это значение большим, чем Rx, или меньшим. В зависимости от этого уменьшить или увеличить величину R0. В дальнейшем следует прибавлять или убавлять целые или десятые доли Ом до тех пор, пока отклонение стрелки гальванометра не станет минимальным. При этом
– в другую. Метод заключается в следующем. Установить на магазине сопротивлений заведомо малое сопротивление (R 0 = 0 Ом). Замкнуть ключ К2. Заметить, в какую сторону отклоняется стрелка гальванометра. Разомкнуть К2. Выставить заведомо большое сопротивление (по указанию преподавателя). Убедиться, что стрелка гальванометра отклоняется в другую сторону. Задать промежуточное значение плеча сравнения (например, R 0 = 5 Ом). По отклонению стрелки определить является это значение большим, чем Rx, или меньшим. В зависимости от этого уменьшить или увеличить величину R0. В дальнейшем следует прибавлять или убавлять целые или десятые доли Ом до тех пор, пока отклонение стрелки гальванометра не станет минимальным. При этом 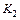 включать лишь на очень короткое время (чтобы только заметить, в какую сторону отклоняется стрелка гальванометра).
включать лишь на очень короткое время (чтобы только заметить, в какую сторону отклоняется стрелка гальванометра).
Точно сбалансировать мост только подбором R0 невозможно из-за конечности минимального значения (шага), на которое его можно изменить. Это минимальное значение для магазина сопротивлений, используемого в данной работе, равняется 0,1 Ом.
3. Произвести точную балансировку моста (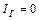 ), передвигая ползунок D вблизи середины реохорда, т. е. меняя отношение
), передвигая ползунок D вблизи середины реохорда, т. е. меняя отношение 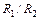 . Определить величину плеча l1.
. Определить величину плеча l1.
4. Повторяя процедуру балансировки при подобранном сопротивлении 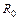 (наиболее близком к
(наиболее близком к 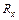 ), получить 5 значений плеча l1.
), получить 5 значений плеча l1.
5. Измерить микрометром диаметр d исследуемой проволоки в 5 различных местах.
6. Повторить все описанные измерения еще для 2-х различных проволок.
Обработка результатов измерений
В случае, если разброс данных превышает погрешность линейки реохорда и микрометра, границы доверительных интервалов ∆ l1 и Δ d находят по алгоритму прямых измерений. Относительные погрешности 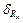 =
= 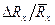 и
и 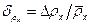 рассчитывают по формулам погрешности косвенных измерений:
рассчитывают по формулам погрешности косвенных измерений:
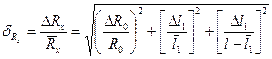 ,
,
где 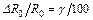 ,
, 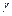 – класс точности магазина сопротивлений, указанный на приборе.
– класс точности магазина сопротивлений, указанный на приборе.
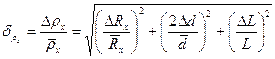 ,
,
Доверительные интервалы искомых величин определяются, соответственно: 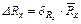 ; ∆
; ∆ 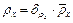 .
.
Окончательный результат представить в виде
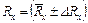 Ом,
Ом, 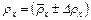 Ом∙м.
Ом∙м.
Вычисления произвести для всех исследованных проводников.
Результаты измерений и расчеты рекомендуется записать в таблицу:
| Материал, из которого изготовлена проволока | 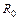 Ом Ом
| Номер опыта | 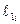 см см
| 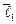 см
см
| 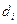 мм
мм
| 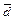 мм мм
| 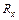 Ом
Ом
| 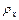 Ом∙м
Ом∙м
|
| Три варианта различных проволок. |
Содержание отчёта
1. Электрическая схема измерений сопротивлений проводников.
2. Сводная таблица экспериментальных данных.
3. Расчёт трех сопротивлений проводников по формуле (31.7).
4. Расчёт удельных сопротивлений проводников по формуле (31.3).
5. Расчёт границ доверительных интервалов (абсолютной погрешности) измерения трех сопротивлений проводников и их удельных сопротивлений.
Контрольные вопросы
s От чего зависит величина удельного сопротивления однородного проводника?
s Если мост сбалансирован, то по каким плечам моста (см. рис. 31.1) будут течь равные токи? Почему нельзя надолго замыкать ключ К2 в схеме на (рис. 31.2)?
s Почему следует работать на середине реохорда АВ (рис. 31.2) при балансировке моста?
Лабораторная работа 32
ОПРЕДЕЛЕНИЕ ЭДС И НАПРЯЖЕНИЙ КОМПЕНСАЦИОННЫМ МЕТОДОМ
Задачи работы
1. Определение ЭДС элемента при комнатной температуре компенсационным методом.
2. Определение внутреннего сопротивления элемента.
Физическое обоснование эксперимента
Закон Ома для полной цепи
Согласно закону Ома для полной цепи электродвижущая сила (ЭДС) источника тока равна сумме падений напряжения на внешнем и внутреннем участках цепи:
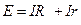 ,
,
где I – ток в цепи, R – сопротивление внешней цепи, 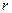 – внутреннее сопротивление источника тока, E – ЭДС источника тока. Если R>>r, то напряжение во внешней части цепи приближается по своему значению к ЭДС источника: E ≈ IR. Отсюда следует, что ЭДС равна разности потенциалов между полюсами разомкнутого источника тока. Поэтому для измерения ЭДС источника тока необходимо применить метод, при котором ток в цепи источника отсутствует, например метод компенсации. – внутреннее сопротивление источника тока, E – ЭДС источника тока. Если R>>r, то напряжение во внешней части цепи приближается по своему значению к ЭДС источника: E ≈ IR. Отсюда следует, что ЭДС равна разности потенциалов между полюсами разомкнутого источника тока. Поэтому для измерения ЭДС источника тока необходимо применить метод, при котором ток в цепи источника отсутствует, например метод компенсации.
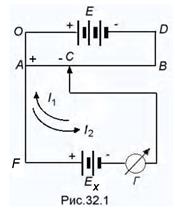
| 
|






