Расчёт добавочного сопротивления к вольтметру

Описания лабораторных работ Учебной лаборатории физического эксперимента физического факультета СПбГУ

Часть IV

ЭЛЕКТРИЧЕСТВО

ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

 

 

Санкт-Петербург 2007

 

ББК 22.33

 

Печатается по постановлению Ученого совета физического факультета СПбГУ.

Ответственные редакторы: В.И. Коротков, Е.П. Зароченцева

 

Авторы: А.В. Бармасов, И.С. Бобкова, С.О. Высоцкая, Б.Д Катунин, Т.Н. Компаниец, Т.К. Крутицкая, Н.А. Малешина, Т.В. Рудакова, В.Е. Тер-Нерсессянц

Составитель: Т.В. Рудакова

 

Рецензент: кандидат.физ.-мат. наук, снс, Л.Л. Басов (СПбГУ)

 

Описания лабораторных работ Учебной лаборатории физического эксперимента физического факультета СПбГУ. Часть IV: Электричество. Постоянный электрический ток / А.В. Бармасов, И.С. Бобкова, С.О. Высоцкая и др.;

Под ред. В.И. Короткова, Е.П. Зароченцевой;

СПб., 2007. – 93 с.

 

Данное пособие содержит описания лабораторных работ по разделу «Электричество. Постоянный электрический ток» курса общей физики и представляет собой существенно переработанное и дополненное переиздание учебного пособия «Электричество (постоянный ток). Ч. 4. / Под ред. В.Е. Холмогорова и Ю.Г. Шишкина» (Л.: Изд-во ЛГУ, 1988. –104 с.). Каждая лабораторная работа рассчитана на 4 академических часа. Студент допускается к выполнению лабораторной работы после самостоятельного изучения необходимой теории, ознакомления с порядком выполнения основных операций и сдачи зачёта по технике безопасности. Предназначено для студентов факультетов: биолого-почвенного, географии и геоэкологии, геологического, медицинского, физического, химического и др.

ББК 22.33

Ó А.В. Бармасов,

И.С. Бобкова,

С.О. Высоцкая и др., 2007

Ó Санкт-Петербургский

государственный

университет, 2007.

СОДЕРЖАНИЕ

 

1. Электроизмерительные приборы
Классификация электроизмерительных приборов
Определение погрешности измерения на электроизмери-тельных приборах. Класс точности прибора.
Масштабные измерительные преобразования (МИП)
Лабораторная работа 31 Исследование проводников 1-го рода с помощью моста постоянного тока
Лабораторная работа 32 Определение ЭДС и напряжений методом компенсации
Лабораторная работа 33 Определение емкостей конденсаторов и ЭДС гальванических элементов при помощи гальванометра
Лабораторная работа 34 Изучение закономерностей прохождения электронов в вакууме. Закон степени трех вторых. Определение удельного заряда электрона
Лабораторная работа 35 Изучение работы трехэлектродной лампы
Лабораторная работа 36 Изучение работы однолучевого электронного осциллографа С1-54
Лабораторная работа 38 Определение удельного заряда электрона методом магнитной фокусировки электронного пучка
Лабораторная работа 39 Определение горизонтальной составляющей магнитного поля Земли.
Приложения
Аналоговые электроизмерительные приборы
Краткая характеристика электроизмерительных приборов наиболее распространенных систем
Литература

ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ

 

Измерение – это нахождение опытным путём с оцененной точностью значения заранее выбранной физической величины путем сравнения ее с эталонной величиной. Электрические измерения осуществляются с помощью электроизмерительных приборов (ЭИП).

Объектами электрических измерений могут быть как электрические и магнитные величины, так и неэлектрические величины (такие, например, как давление, скорость, температура). Для того чтобы измерить неэлектрическую величину с помощью электроизмерительных приборов, ее надо преобразовать в зависящую от нее электрическую величину. Устройства для измерения неэлектрических величин должны содержать преобразователь, соединительные провода и электроизмерительный прибор, шкала которого проградуирована в единицах измеряемой величины.

В качестве одного из наиболее простых примеров можно привести измерение температуры с помощью термопары. Величина электродвижущей силы (эдс) термопары зависит от разности температур между горячим и холодным спаями, т. е. термопара является в данном случае преобразователем. С помощью проводов к ней подключается милливольтметр, измеряющий эдс термопары (термоЭДС). В этом случае шкалу милливольтметра можно проградуировать в единицах температуры.

 

Классификация электроизмерительных приборов

 

ЭИП можно классифицировать по различным признакам:

По характеру снимаемых показаний измеряемой величины.

Показывающие ЭИП. Это приборы, предварительно отградуированные и позволяющие производить по шкале отсчет численного значения измеряемой величины. С помощью таких приборов можно сразу получить значение измеряемой величины.

Регистрирующие ЭИП. Эти приборы допускают считывание и регистрацию или только регистрацию показаний. К таким приборам относятся самопишущие приборы, дающие запись показаний в виде диаграммы, печатающие приборы, которые печатают показания в цифровой форме, а также осциллографы. Для получения значений измеряемой величины такие приборы требуют специальной градуировки.

По способу преобразования измеряемой величины и способу считывания показаний.

Аналоговые ЭИП. В этих приборах показания являются непрерывными функциями изменений измеряемых величин.

Примером аналогового прибора может служить стрелочный амперметр (рис. 1).

Рис. 1.

При увеличении тока стрелка амперметра смещается плавно. Тем не менее, плавность изменения показаний не означает, что величина тока может быть измерена с любой точностью (см. ниже).

Цифровые приборы. В таких приборах непрерывно изменяющийся измеряемый параметр преобразуется в дискретный параметр (число), которое отображается на его отсчетном устройстве – панели цифровой индикации (рис. 2).

Рис. 2.

При плавном изменении тока показания прибора изменяются дискретно.

Приборы сравнения. Это приборы, предназначенные для непосредственного сравнения измеряемой величины с величиной, значение которой известно. К таким приборам относятся, например, мосты, потенциометры, компенсаторы напряжения и тока.

Простейшим примером схемы сравнения может служить компенсатор напряжения. Принцип работы компенсатора напряжения показан на рис. 3.

Рис. 3.

ЭДС источников равны, когда показание гальванометра равно нулю. Основное достоинство такого способа измерения состоит в том, что в этом случае не происходит отбора тока от источника. Этот способ удобен для измерения ЭДС источников с большим внутренним сопротивлением.

Особенно хорошо видны преимущества методов сравнения при измерении сопротивлений. Можно определить сопротивление, воспользовавшись амперметром и вольтметром (R = U / I). Такой способ (способ амперметра и вольтметра) является наиболее простым, но наименее точным из-за присущей ему систематической ошибки.

Два варианта включения измерительных приборов показаны на рис. 4. На рис. 4, а приведена схема «правильная по напряжению», но амперметр показывает сумму токов, текущих через вольтметр и нагрузку. На рис. 4, б – схема «правильная по току», но вольтметр показывает сумму падений напряжения на амперметре и нагрузке.

Рис. 4.

Широкое применение для измерения сопротивлений получили мосты, питаемые постоянным током, так как их уравновешивание несложно и подбор подходящего гальванометра не составляет особого труда.

Примером такой схемы сравнения может служить четырёхплечевой мост постоянного тока, применяемый для измерения сопротивлений (рис. 5).

Рис. 5.

В одно из плеч моста включен неизвестный резистор R_X. При измерении сопротивления таким методом, неизвестное сопротивление сравнивается с известными сопротивлениями моста, а включенный в одну из диагоналей моста гальванометр Г служит индикатором отсутствия тока.

Точность измерения в данном случае определяется точностью значений известных сопротивлений и чувствительностью гальванометра.

Мосты переменного тока применяются, в основном, для измерения индуктивностей и емкостей.

Определение погрешности измерения на электроизмерительных приборах. Класс точности прибора

Следует помнить, что никакое измерение, т. е. сравнение с эталонной величиной, не может быть выполнено абсолютно точно. Результат измерения всегда содержит некоторую ошибку. Кроме того, надо учесть, что измерение проводится не путем сравнения с самим эталоном, а с помощью измерительного прибора (который при поверке сравнивается с эталоном). Очевидно, что, измеряя с помощью этого измерительного прибора, мы не можем сделать ошибку меньше, чем та, которая определяется погрешностью измерительного устройства.

Разность между показаниями прибора и действительным значением измеряемой величины называется абсолютной погрешностью D А.

D А = ê А ИЗМ – А ДЕЙСТ ê.

(1)

Отношение абсолютной погрешности к действительному значению измеряемой величины, выраженное в процентах, называется относительной погрешностью:

.

(2)

Приведенные определения относительной и абсолютной погрешности не дают возможности узнать их величину, так как действительное значение измеряемой величины нам неизвестно. Определить величины погрешностей при электрических измерениях становится возможным, если известен класс точности прибора (g_КЛ.Т.). Он дает предельную абсолютную погрешность, выраженную в процентах, от номинального показания прибора (максимального при данном пределе измерения) А _НОМ:

.

(3)

Класс точности указан на шкале прибора (см. Рис. 6).

Зная класс точности прибора, можно легко определить абсолютную погрешность измерения D А:

.

(4)

Например, для катушки сопротивления в 1000 Ом класса точности 0,05 абсолютная погрешность:

.

Относительную погрешность также можно вычислить через класс точности прибора. По определению относительная погрешность:

.

(5)

Учитывая, что действительное значение измеряемой величины А _ДЕЙСТ и показания прибора А _ИЗМ примерно равны (А _ДЕЙСТ» А _ИЗМ), и, используя формулу (4), получим:

.

(6)

Видно, что относительная погрешность измерений будет тем меньше, чем ближе снимаемые показания к номинальному значению для данного прибора, то есть к концу шкалы. Следовательно, при работе с многопредельными ЭИП нужно так выбирать предел измерения прибора, чтобы показания считывались со второй половины шкалы. Следует помнить, что номинальное значение многопредельного ЭИП определяется положением, в котором стоит переключатель пределов при данном измерении.

При работе с многопредельными приборами нужно внимательно рассчитывать цену одного деления шкалы Ц_Д. Под ценой деления следует понимать не разность между штрихами, а разность между ними в соответствии с оцифровкой шкалы. Цена деления равномерной шкалы равна отношению номинального значения показания прибора (предела измерения) к общему числу делений N на шкале прибора: Ц_Д = . Численное значение измеряемой величины А _ИЗМ равно цене деления Ц_Д, умноженной на измеренное число делений N _ИЗМ по шкале:

А ИЗМ = ЦД· N ИЗМ.

(7)

Рассмотрим примеры определения погрешностей для многопредельных ЭИП.

Пример 1.
Переключа-тель пределов измерения	→		←   ←	Шкала прибора Класс точности gКЛ.Т. (0,5)
Рис. 6.

На рис. 6 изображён многопредельный вольтметр. Вычислим абсолютную и относительную погрешности определения напряжения. Класс точности вольтметра 0,5.

Номинальное значение напряжения 300 В (определяется положением переключателя пределов напряжения).

Цена деления данного предела измерения Ц_Д = = 2 В/дел.

Измеренное значение напряжения U _ИЗМ = 2 В/дел.·75 дел. = 150 В.

Абсолютная погрешность измерения D U = = 1,5 (В).

Относительная погрешность измерения g₀ = = 1,0%.

Пример 2. Рис. 7.

На рис. 7 изображен тот же многопредельный вольтметр при другом положении переключателя пределов измерений. Вычислим абсолютную и относительную погрешности определения напряжения.

Номинальное значение напряжения 150 В.

Цена деления данного предела измерения Ц_Д = 150 В / 150 дел. = 1 В/дел.

Измеренное значение напряжения U _ИЗМ = 1 В/дел.×150 дел. = 150 В.

Абсолютная погрешность измерения D U = 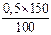= 0,75 (В).

Относительная погрешность измерения g₀ = = 0,5%.

Таким образом, выбор наиболее подходящего предела измерения приводит к уменьшению как абсолютной, так и относительной погрешности.

 

Масштабные измерительные преобразователи (МИП)

 

При необходимости измерения токов и напряжений, превышающих верхний предел измерения используемого прибора, используются МИПы.

Для приборов постоянного тока в качестве МИП используются шунты и добавочные сопротивления. Для приборов переменного тока - добавочные резисторы и измерительные трансформаторы тока и напряжения.

Расчёт шунта к амперметру

 

При измерении тока амперметр включается последовательно с нагрузкой. Если амперметром требуется измерить ток, превышающий верхний предел измерения, то параллельно амперметру включается шунт с сопротивлением R _Ш (рис. 8). Шунт представляет собой толстую константановую или манганиновую пластину. Применение этих сплавов для изготовления шунтов связано с тем, что их сопротивление слабо зависит от температуры.

Рис. 8.

На рис. 8 показана схема подключения шунта R _Ш к амперметру. R _А – внутреннее сопротивление амперметра, которое мало по сравнению с сопротивлением нагрузки R _Н для того, чтобы включение амперметра последовательно с нагрузкой не приводило к существенным изменениям тока в цепи нагрузки. I – ток через сопротивление нагрузки R _Н; I _Ш – ток через шунт с сопротивлением R _Ш; I _А – ток через амперметр с сопротивлением R _А.

По первому правилу Кирхгофа алгебраическая сумма токов в узле равна нулю:

I = I _А + I _Ш

и, следовательно,

I _Ш = I – I _А.

Падение напряжения между точками а и b:

U_аb = I _А· R _А = I _Ш· R _Ш.

Таким образом, для того, чтобы с помощью данного амперметра измерить ток I, сопротивление шунта должно быть:

,

(8)

где: I / I_A = n – коэффициент шунтирования, показывающий, во сколько раз расширяется предел измерения амперметра при подключении шунта.

Фактический ток в цепи определяется произведением показаний прибора и множителя n.

Рис. 9.

Реальный шунт (рис. 9) должен иметь четыре контакта: к двум из них подключается прибор, а к двум другим – соединительные провода электрической цепи.

 

Пример 3.

Рассчитаем шунт к миллиамперметру на 10 m А с внутренним сопротивлением 500 Ом, если надо измерить ток 10 А.

Воспользуемся формулой (8):

 

Расчёт добавочного сопротивления к вольтметру

 

Для измерения напряжения вольтметр включается параллельно с нагрузкой. Если вольтметром требуется измерить напряжение, превышающее верхний предел измерения, то последовательно вольтметру включают добавочное сопротивление R _Д.

Рис. 10.

На рис. 10 показана схема подключения добавочного сопротивления R _Д к вольтметру. R _V – внутреннее сопротивление вольтметра. Оно должно быть большим по сравнению с сопротивлением нагрузки R _Н для того, чтобы включение вольтметра параллельно нагрузке не приводило к существенным изменениям напряжения на нагрузке. U _ИЗМ – измеряемое напряжение; U _НОМ – предел измерения вольтметра.

Ток, текущий через вольтметр:

,

следовательно, добавочное сопротивление должно быть:

.

(9)

 

Пример 4.

Рассчитаем добавочное сопротивление к вольтметру на 100 В для измерения напряжения 300 В. Внутреннее сопротивление вольтметра R _V = 3000 Ом.

.

Добавочные сопротивления могут служить и для преобразования рода измеряемой величины (напряжения в ток и наоборот). Рассмотрим, как измерить напряжение с помощью амперметра. Для этого последовательно с амперметром включается большое сопротивление R _Д (рис. 11).

Рис. 11.

Неизвестное напряжение U _X = I _А·(R _Д + R _А), где R _А – внутреннее сопротивление амперметра. Если величины внутреннего и добавочного сопротивлений известны, то, измеряя ток с помощью амперметра, легко вычислить искомое напряжение.

 

Читайте также раздел «Приложения».

 

Лабораторная работа 31