Principal concepts of the theory of errors

Частина 1

Для студентів інженерно-технічних спеціальностей

денної форми навчання

 

Методичні вказівки до лабораторних робіт з фізики. Механіка. Молекулярна фізика. Частина 1. Для студентів інженерно-технічних спеціальностей денної форми навчання / Укладачі: Лоскутов С.В., Єршов А.В., Серпецький Б.О., Правда М.І., Манько В.К., Лущін С.П., Курбацький В.П., Работкіна О.В., Денисова О.І. – Запоріжжя: ЗНТУ, 2009. - 90 с.

 

 

Укладачі: Лоскутов С.В., професор, д-р. фіз.-матем. наук.; Єршов А.В. канд. техн. наук, доцент; Серпецький Б.О., канд. фіз.-матем. наук, доцент; Правда М.І., канд. фіз.-матем. наук, доцент; Манько В.К.., канд. фіз.-матем. наук, доцент; Лущін С.П., канд. фіз.-матем. наук, доцент; Курбацький В.П., канд. фіз.-матем. наук, доцент; Работкіна О.В., старший викладач; Денисова О.І., старший викладач.

 

Р е ц е н з е н т и: Корніч В.Г., канд. фіз.-матем. наук; Золотаревський І.В., канд. фіз.-матем. наук, доцент; Сокол Т.О., старший викладач кафедри іноземної мови.

 

Затверджено на засіданні кафедри фізики ЗНТУ,

протокол № 10 від 04.07.2011 р.

 

 

Методичні вказівки до лабораторних робіт з фізики “Механіка. Молекулярна фізика. Частина 1” схвалені на засіданні Методичної Ради Електротехнічного факультету ЗНТУ, протокол № 5 від ” 27 ” січня 2011 р.

 

Відповідальний за випуск: Єршов А.В., докт. техн. наук, професор.

 

ЗМІСТ

 

Частина 1

Вступ …………………………………………………………………….. 6

1 Елементи теорії похибок ……………………………………………... 7

1.1 Основні поняття теорії похибок ……………………………………. 7

1.2 Похибки засобів вимірювання ……………………………………..11 1.3 Похибки табличних величин..…………………………….……. 12 1.4 Правила округлення і виконання наближених обчислень …..... 12 1.5 Похибки прямих вимірювань ……………………………………... 14

1.6 Похибки непрямих вимірювань …………………………………... 15

1.7 Графічне відображення експериментальних результатів …… 16 Контрольні запитання ……..…………………………………………... 17

2 Elements of the theory of errors …………………………………… 18 2.1 Principal concepts of the theory of errors …………………………… 19

2.2 Errors of instruments ………………………………………………. 20 2.3 Error of table quantities, count and rules of approximations...…...... 21 2.4 Errors of direct measurement ………..…………………………...... 21 2.5 Errors of indirect measurements …………………………..………… 22 2.6 Graph presentation of the experimental results …………….……...... 24 Control questions …………………………………….……….………… 24

3 Лабораторна робота № 1. Визначення густини тіл ………………... 25 3.1 Вступ ………………………………………………………………... 25 3.2 Вимірювання і визначення похибок ……………………………... 29 Контрольні запитання ……………..………………………..………… 31 4 Laboratory work № 1. Definition of a body density..………………… 34 4.1 System International Units …..……………………………………. 34 4.2 Volume ……………………………………………………………… 35 4.3 Vernier scale ………………………………………………………… 35 4.4 Micrometer screw gauge ………………………………………........ 36 4.5 Measurement of mass …………..………………………………….. 37 4.6 Measurement of weight …………………………………………….. 38 4.7 Experimental part …………………………………….……….…...... 39

5 Лабораторна робота № 2. Визначення модуля Юнга металів...... 41 5.1 Вступ…………………………….………………………………....... 41

5.2 Опис установки ……………………………………………………. 44 5.3 Порядок виконання роботи ……….………………………………. 44

 

Контрольні запитання ………………………………….…………….. 46 6 Laboratory work № 2. Measuring of Yung modulus of metals.……… 47 6.1 Introduction …………….…………………………………………. 47 6.2 Experimental device …………………….………………………...... 49 6.3 Experimental part ……………………………………………….... 50 Control questions ………….…………………………….…………........ 52

Literature ………………………………………………….…………… 52 7 Лабораторна робота № 3. Визначення коефіцієнта внутрішнього

тертя методом Стокса ………………………….……….………… 53 7.1 Опис установки ………………………...……………. …………… 53

7.2 Теорія методу Стокса …………………………....……….……… 53 7.3 Порядок виконання роботи (завдання 1) …....………………..…... 54

7.4 Порядок виконання роботи (завдання 2) ……….………………. 55 Контрольні запитання …………………………………..…………....... 57

8 Laboratory work № 3. Measuring the coefficient of internal friction

by Stocks’ method ……………………………...……………………58 8.1 Theory ………………………………………………...…………... 58 8.2 Experimental part ……………………………………...……………. 59 Control questions ………………………………………...…………........ 60 9 Лабораторна робота № 4.1 Пружний удар куль..…………………. 61

9.1 Коротка теорія пружного удару ……………………...…………. 61 9.2 Порядок виконання роботи ……………………………...………... 64

Контрольні запитання ……………….……………………………… 66 10 Лабораторна робота № 4.2. Пружний і непружний удари куль … 67 10.1 Основні положення …………………………………………… 67 10.2 Порядок виконання роботи ……………………………………… 72

Контрольні запитання …………………………………………………. 73 Список літератури ……………………………………………………... 73

11 Laboratory work № 4. Elastic impact of bodies.................................. 74 11.1 Task ……………………………………………………………... 74 11.2 Short theory...………………………………………………….... 74 11.3 Elastic impact ……………………….…………………………... 75 11.4 Experimental part ……………………………………………….. 77 Control questions ……………………………………………………… 77 12 Лабораторна робота № 4.3. Непружний удар тіл ………………… 79

12.1 Коротка теорія непружного удару …………………………….. 79 12.2 Порядок виконання роботи …………………………………… 81 Контрольні запитання …………...……………..……………………. 82 13 Laboratory work № 4.3. Inelastic impact of bodies ………………..84 13.1 Short theory of inelastic impact …………… …………………….84 13.2 The sequence of performing the work ………………………….. 87 Control questions …………………………………………………….. 88 Literature ………………………………….…………………………….. 88

Частина 2

 

ВСТУП

 

Збірник містить лабораторні роботи для студентів усіх спеціальностей.

Основна спрямованість методичних вказівок з предмету фізика - дати можливість студентам за допомогою досліду вивчити важливі фізичні явища. Опис лабораторних робіт не претендує на те, щоб створити у студентів повне уявлення про явища, які вивчаються. Таке уявлення може виникнути лише внаслідок опрацювання лекцій та підручників.

Велика увага в методичних вказівках з фізики для студентів технічних спеціальностей приділяється обробленню результатів вимірювання. Для успішного виконання робіт необхідна попередня самостійна підготовка, в першу чергу теоретична.

Кожна лабораторна ро­бота розрахована на дві академічні години занять у лабораторії. Перед заняттям студент повинен підготувати протокол ла­бораторної роботи, вивчивши відповідний теоретичний матері­ал.

Під час заняття студенти проводять необхідні виміри, виконують розрахунки, доводять звіт до висновку. Результати вимірювання обговорюються з викладачем і затверджуються.

Повністю оформлений звіт по лабораторній роботі потрібно подати виклада­чу до кінця заняття. Він повинен містити: титульний лист, номер лаборато­рної роботи та її назву, перелік приладів і приладдя, мету робо­ти, схему установки, розрахункові формули, таблицю результа­тів вимірів і розрахунки, висновки за результатами роботи. Графіки повинні бути виконані на мі­ліметровому папері.

Якщо студент не встигає захистити лабораторну роботу до кінця заняття, дозволяється оформити звіт (графіки) з використанням комп’ютерних програм (Excel, Origin) до наступного заняття.

Лабораторна робота вважається виконаною після успішно проведеного захисту шляхом співбесіди студента з викладачем (захист звіту + оцінка за теоретичний матеріал).

Захист звіту: мета роботи + експериментальна методика + висновки.

Теоретичний матеріал: знання фізичних явищ, які вивчалися у даній лабораторній роботі (закони, формули).

 

1 ЕЛЕМЕНТИ ТЕОРІЇ ПОХИБОК

1.1 Основні поняття теорії похибок

 

Числове значення будь-якої фізичної величини знаходять шляхом виміру, або розрахунку. Вимірювання це процес відшукання значення фізичної величини дослідним шляхом за допомогою спеціальних технічних засобів. Виміряти безпосередньо якусь фізичну величину цс означає порівняти її з деякою іншою однорідною з нею величи­ною, взятою за одиницю виміру. Отримане число показує, у скі­льки разів величина, що вимірюється, більше або менше обраної одиниці виміру. Отриманому числу приписується таке ж на­йменування, як і обраній одиниці.

Прямі виміри здійснюються або шляхом безпосереднього порівняння фізичної величини, що вимірюється, з одиницями міри, як це має місце при вимірах довжини лінійкою, штанген­циркулем, мікрометром і т.п., або приладами, градуйованими у визначених одиницях, наприклад амперметрами, вольтметрами і т.п.

В багатьох випадках значення фізичної величини визначають за допомогою обчислень, використовуючи при цьому значення безпосередньо виміряних величин. Це трапляється тоді, коли відома функціональна залежність даної величини від безпосередньо виміряних величин. Наприклад, для визначення об’єму циліндра використовують функціональну залежність від діаметра d та висоти h:

.

При непрямих вимірах, величину y знаходять по відомій функціональній залежності y = f(x_1, x₂,...,x_n) від величин x₁, x₂, … x_n, значення котрих знаходять прямими вимірами.

Виміряне значення фізичної величини завжди відрізняється від істинного тому, що при вимірюваннях завжди виникають похибки. При вимірюваннях необхідно знайти не тільки наближене значення фізичної величини, але й обчислити відхилення цього значення від істинного. Цим питанням займається теорія похибок.

Всі вимірювання можуть бути виконані тільки з визначеним ступенем точності. Похибка вимірювань визначається як відхилення результату виміру від істинного значення величини.

Як показує теорія і практика, до істинного значення вимірюваної ве­личини найближче підходить середнє арифметичне значення ба­гатьох вимірювань. Якщо якусь величину х виміряли n раз і отримали ряд значень х₁, х₂... х_n, то найбільш ймовірне значення виміряної величини х знаходять як середнє арифметичне результатів окремих вимірів:

. (1.1)

Похибки вимірів бувають систематичними, випадковими і промахами.

Систематична похибка – це складова частина похибки виміру, що залишається сталою, або такою, що закономірно змінюється при повторних вимірах однієї та тієї ж величини.

Випадкова похибка – це складова частина похибки вимірювань, що змінюється випадково при повторних вимірах однієї та тієї ж величини.

Промах – це такий результат виміру, значення якого набагато відрізняється від очікуваної похибки в даних умовах. Наприклад, ці похибки можуть бути отримані, якщо прилад несправний або якщо експериментатор неуважний.

Похибки вимірювань бувають абсолютними і відносними. Абсолютною похибкою вимірювання називається похибка, виражена в одиницях величини, що вимірюється, вона визначається формулою

, (1.2)

де х – значення, здобуте при вимірюванні; Х – справжнє значення величини, що вимірюється (найбільш ймовірне).

Середня арифметична абсолютна похибка n вимірювань дорівнює

. (1.3)

Величина визначає інтервал, у межах якого з певною ймовірністю знаходиться істинне значен­ня вимірюваної величини. За визначенням

., (1.4)

де Δx – абсолютна похибка вимірювань x. Чим більша ширина інтервалу 2Δx, тим більшою буде ймовірність того, що точне значення вимірюваної величини належить цьому інтервалу.

Відносною похибкою вимірювання називається відношення абсолютної похибки вимірювання до справжнього значення величини що вимірюється

, (1.5)

як правило, визначається у відсотках

. (1.6)

Знайти істинне значення фізичної величини х неможливо. Можна тільки вказати на інтервал (х_min, х_max), в якому з ймовірністю a знаходиться значення досліджуваної величини.

Приклад: поглядом вимірюють зріст студента в сантиметрах. Ми можемо припустити, що зріст студента може бути визначений між 1,5 м і 2,0 м з ймовірністю 0,9. Тоді ми можемо стверджувати, що зріст студента може бути визначений між 1,6 м і 1,8 м з меншою ймовірністю 0,6 і так далі. Цей інтервал називають довірчим інтервалом. На рис.1.1 зображено довірчий інтервал досліджуваної величини x, де – найбільш ймовірне значення виміряної величини; Δх – півширина довірчого інтервалу для заданого a. Тому, істинне значення вимірюваної величини може бути визначене як

, (1.7)

з ймовірністю a, або

. (1.8)

 

Рисунок 1.1

 

Ймовірність знаходження істинного значення вимірюваної величини в інтервалі Dx залежить від кількості вимірювань n. Якщо , то ймовірність наближається до 1. Якщо ж n до­рівнює кільком одиницям, то ймовірність не досягає й 0,6. Тому для малої кількості вимірювань згаданий інтервал розширю­ють, збільшуючи Δx. Для цього знаходять середньоквадратичну похибку середнього арифметичного

, (1.9)

 

і збільшують її в t раз (t – так званий коефіцієнт Ст`юдента. Цей коефіцієнт було введено в 1908 році англійським математиком та хіміком В.С. Госсетом). Величину

, (1.10)

називають випадковим відхиленням. Середнє квадратичне похибка результату серії вимірювань, викликана випадковими відхиленнями Dx_i, визначається як

. (1.11)

 

Множимо знайдене значення коефіцієнта Стьюдента t (коефіцієнт Стьюдента, залежить від a і кількості вимірів n) на середню квадратичну похибку середнього значення, знаходимо випадкову похибку Δх_вип результатів прямих вимірювань

. (1.12)

 

 

Таблиця 1.1

n\α	0,4	0,5	0,6	0,7	0,8	0,9
	0,73	1,00	1,38	2,0	3,1	6,3
	0,62	0,82	1,06	1,4	1,9	2,9
	0,58	0,77	0,98	1,3	1,6	2,4
	0,57	0,74	0,99	1,2	1,5	2,1
	0,56	0,73	0,92	1,2	1,5	2,0
	0,55	0,72	0,91	1,1	1,4	1,9
	0,55	0,71	0,90	1,1	1,4	1,9
	0,54	0,71	0,89	1,1	1,4	1,9
	0,54	0,70	0,88	1,1	1,4	1,8
	0,58	0,69	0,86	1,1	1,3	1,7
∞	0,52	0,67	0,84	1,0	1,3	1,6

 

1.2 Похибки засобів вимірювання

 

До засобів вимірювань належать вимірювальні прилади та установки. Кожен прилад дає похибку, так як його неможливо зробити ідеальним. Похибка засобів вимірювання не перевищує деякої величини. Цю величину називають межею основної допустимої похибки вимірювального приладу (МОДП). МОДП на засоби вимірювання встановлюється державними стандартами і визначається у вигляді абсолютних, відносних та приведених похибок.

Абсолютна похибка приладу d – це є різниця

, (1.13)

де a – показання приладу, X – справжнє значення вимірюваної величини. Взагалі d дорівнює ціні найменшої поділки інструмента. Наприклад: для лінійки d =1 мм. Відносна похибка вимірів – це відношення

. (1.14)

Як правило, вона визначається у відсотках

. (1.15)

Приведена похибка вимірювання або клас точності визначається відношенням

, (1.16)

і визначається у відсотках. D – максимальне значення шкали інструмента. Наприклад: сила струму вимірюється амперметром з діапазоном 0 ÷ 1 А, клас точності 0,5. Це означає, що Х_н = 1 А; γ = 0,5 % і

.

Якщо амперметр показує 0,3 А, тоді

.

 

Похибки табличних величин

 

1. Похибка табличної величини визначається за формулою

, (1.17)

де a - довірча ймовірність; ν - половина ціни розряду останньої залишеної цифри табличної величини. Наприклад: величина π дорівнює 3,14. В цьому випадку ν = 0,005 і

.

Якщо величина π дорівнює 3,141 і ν = 0,0005, то

.

2. При користуванні вимірювальними приладами виникають похибки відліку. Типово, похибка відліку дорівнює половині ціни поділки шкали приладу. Наприклад: лінійка має похибку відліку ν = 0,5 мм.

 

1.4 Правила округлення і виконання наближених обчислень

 

Точність обчислень завжди повинна відповідати точності вимірів. Зайва арифметична точність обчислень не позитивна якість, а недолік в роботі. Наприклад, якщо середнє арифметич­не значення товщини пластинки після розрахунку було взято рі­вним 2,2543 мм при абсолютній похибці вимірів 0,03 мм, то при цьому показане лише невміння виконувати арифметичні дії з на­ближеними числами. Щоб не витрачати даремно часу для одер­жання сумнівної арифметичної точності, необхідно всі отримані величини перед підстановкою в формули округляти, залишаючи в них на одну значущу цифру більше, ніжу самої з наближених величин (з найменшим числом знаків). При округленні набли­женого числа необхідно відкидати останні цифри, якщо перша з цифр, що відкидаються, менша 5, і додавати одиницю до попе­редньої цифри, якщо перша з цифр, що відкидаються, 5 або бі­льше.

За написаним числом, що виражає результат виміру або об­числення, можна говорити про ступінь точності.

Значущі цифри – це усі цифри, крім нулів, що стоять перед числом, і нулів, поставлених наприкінці записаного результату замість відкинутих цифр при округленні.

Десяткові таки числа – це усі цифри, розміщені праворуч від коми. Наприклад, число 25,002 має п'ять значущих цифр, а десяткових знаків три; число 0,0034 має дві значущі цифри, але чотири десяткових знаки.

Якщо обчислення за наближеними даними проводяться у декілька дій, то в проміжних діях треба зберігати на одну значу­щу цифру більше в порівнянні з точністю визначуваних величин у даному досліді (тобто дві сумнівні цифри). У всіх арифметичних діях над наближеними числами в ос­таточному результаті треба уберігати стільки десяткових знаків, скільки їх мають наближені дані з найменшим числом десяткових знаків.

Округлення чисел у процесі обчислення призводить до систематичної похибки. Відносна похибка, яку знаходять в результаті обчислень, має бути приблизно на порядок (тобто у 10 разів) менша за похибку результату непрямих вимірювань.

У записі результату вимірювань залишають одну (максимум дві) сумнівні цифри. Похибку вимірювань округляють до однієї значущої цифри, якщо ця цифра не «1». Якщо ж ця цифра «1», то у похибці залишають дві значущі цифри, в записі результату вимірювань – дві сумнівні цифри. Сумнівними називаються значущі цифри в записі результату вимірювань, десяткові розряди яких збігаються з десятковими розрядами значущих цифр у записі похибки цього результату.

Розряди останніх цифр Δx і x мусять співпадати. Для цього округляють x або приписують до нього невистачаючі нулі справа. Е округляють по тим же правилам, що і Δx. Спочатку округляють Δx, Δx=0,3 мм. Розряд останньої цифри Δx - десяті долі, а – соті долі. Округляємо до десятих долів. Маємо = 73,6 мм.

Знаходимо Е:

Кінцевий результат x = 173,6 ± 0,3 мм, α = 0,7, Е = 0,4 %

 

1.5 Похибки прямих вимірювань

 

Похибки прямих вимірювань визначаються за формулою

, n = 1, (1.18)

якщо деяку величину виміряти один раз.

Якщо вимірювання виконувались n раз, то

, n > 1. (1.19)

В цих рівняннях t_∞ - коефіцієнт Стьюдента для заданого a при необмеженому числі вимірів; d - похибка приладу; ν - похибка відліку, .

Наприклад: довжина тіла була виміряна 3 рази:

 

n	х, мм	∆хi, мм	(Δхi)²
	12,8	0,446	0,217
	13,6	0,334	0,111
	13,4	0,134	0,018
=13,2	∑(Δхi)²=0,3

 

Відносна похибка дорівнює

.

Кінцевий результат: x = (13,3 ± 0,3) мм; α = 0,7; Е = 3,6 %.

 

1.6 Похибки непрямих вимірювань

 

Якщо y - величина, що вимірюється посередньо, її розраховують за відомою залежністю y=f(x₁,x₂,…x_n) від змінних x₁,x₂,,…x_n, які вимірюють безпосередньо.

1. Похибки непрямих вимірів визначаються за формулою:

, (1.20)

якщо функціональна залежність досліджуваної величини є багаточлен.

2. Похибки непрямих вимірів можна визначати

, (1.21)

.

якщо функціональна залежність досліджуваної величини є одночлен і потім знаходимо Dy як: 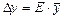. Наприклад:

1. Якщо залежність функції , тоді

Тоді

.

2. Якщо залежність функції: ,

Тоді

,

.

У результаті отримуємо

.

 

1.7 Графічне відображення експериментальних результатів

 

Графік будується на міліметровому папері. На рисунках нижче можна побачити приклади графіків.

 

невірно вірно

 

 

Експериментальна крива проходить крізь експериментальні точки.

Контрольні запитання

 

1. Дати визначення прямих і непрямих вимірів. Приклади.

2. За допомогою якої формули знаходять найбільш ймовірне значення виміряної величини?

3. Що таке відносна похибка?

4. Що називається випадковим відхиленням?

5. За якою формулою знаходять середнє квадратичне значення або похибку, викликану випадковими відхиленнями?

6. За якою формулою знаходять похибки засобів виміру.

7. За якою формулою знаходять похибки табличних величин та відліку.

8. Сформулюйте правила округлення.

9. Запишіть формули обчислення похибок при прямих вимірах.

10. Запишіть формули обчислення похибок при непрямих вимірах.

 

Доповнення і редагування:

доцент кафедри фізики, канд. фіз.-матем. наук В. Г. Корніч;

професор кафедри фізики, д-р. фіз.-матем. наук С. В. Лоскутов.

 

Затверджено на засіданні кафедри фізики ЗНТУ, протокол № 3 від 01.12.2008 р.

 

2 ELEMENTS OF THE THEORY OF ERRORS

 

Measurement of physical quantities means their comparison with standard. There are two types of physical measurements:

1. Direct measurements are measurements when the investigated quantity x is taken by direct comparison with the standard performed with instruments.

2. Indirect measurements consist of direct measurements of physical quantities x₁, x₂,.., x_n and calculations made on this basis the investigated quantity y by a functional dependency y = f(x_1, x₂,...,x_n).

For example: measurements of length by a ruler or measurements of temperature with a thermometer are direct measurements. But measurement of volume of a cylinder by the value of its height h and diameter d (these are direct measurements) with functional relation V=pd²h/4 is an indirect measurement.

All measurements can be performed only up to a certain degree of precision. Error of measurements is defined as a deviation of the result of measurements from the true value of a measured quantity.

Then, by definition

,

where Dx is absolute error of x measures.

The problems of the Theory of Errors are:

1. To get the investigated quantity.

2. To get the error of measurements.

There are two kinds of measurements errors: systematic errors and accidental ones.

Systematic error is defined as a component of error; its quantity is constant in all measurements or is being regularly changed during the repeated measurements of the physical quantity.

Accidental error is defined as a component of error that is changed irregularly during repeated measurements of the same physical quantity.

One should distinguish between blunder and above mentioned errors. Its value is essentially greater than the expected error in given conditions. For example, these errors may be received if an instrument is faulty, or if an experimenter is inattentive and so on.

 

Principal concepts of the theory of errors

 

We can't define the true values of a physical quantity. We can define only the interval (x _min, x _max) of the investigated quantity with some probability a. For example: we can affirm, that students' height may be defined between 1.5 m and 2.0 m with probability of 0.9. Then we can prove, that students' height may be defined between 1.6 m and 1.8 m with smaller probability of 0.6 and so on. Value of this interval is called the entrusting interval. On fig.2.1 interval of quantity being investigated x is represented.

Figure 2.1

 

Where x is the most probable value of quantity being measured; Dx is the half width of the entrusting interval of the measured quantity with probability of a.

Therefore we can estimate, that true value of the measured quantity may be defined as x = x D x, with probability a,

or .

If a quantity x has been measured n times and x₁, x₂,..., x_n are the results of the individual measurements then the most probable measured value or the arithmetic mean is:

(2.1)

The deviation is called the accidental error (deviation) of a single measurement.

(2.2)

is called the mean accidental deviation of the measurements.

Mean root square is defined as

(2.3)

where t – Student’s constant for definite a and n. The ratio of

(2.4)

is called the relative error of measurement and is usually expressed in percents:

. (2.5)

 

Errors of instruments

 

Absolute error of instrumental d is a deviation

, (2.6)

where a is an index of an instrument; X is the true value of the quantity measured. Typically d is quantity of the instruments minimum value scale. For example: the ruler error is d = 1 mm.

Relative error of the measurement is the ratio of

. (2.7)

It is usually expressed in percent

. (2.8)

Brought error of the measurement or precision class is the ratio

, (2.9)

expressed in percent. D is maximum value on the instrument scale.

For example: electric current is measured by the instrument with interval 0 ÷ 1 A, precision class is 0.5. This means, that D = 1 A, g = 0.5 %, and

.

If the instrument shows 0.3 A, then

.